Il fissaidee

11. Isocronismo delle piccole oscillazioni

Nel caso del sistema massa-molla, la forza esercitata dalla molla sulla massa è proporzionale allo spostamento dalla posizione di equilibrio, qualunque sia il modulo di tale spostamento (sia pure entro certi limiti molto ampi, oltre i quali la molla cessa di comportarsi in maniera “ideale” e si può deformare in maniera permanente). Esistono però numerosi sistemi meccanici nei quali il corpo è soggetto a una forza di richiamo che non è strettamente proporzionale allo spostamento dalla posizione di equilibrio. Alcuni esempi sono mostrati in figura: un pendolo semplice, una pallina libera di rotolare in prossimità del fondo tondeggiante di una scodella, una pallina fissata al centro di una corda di chitarra mantenuta tesa tra due estremi. 

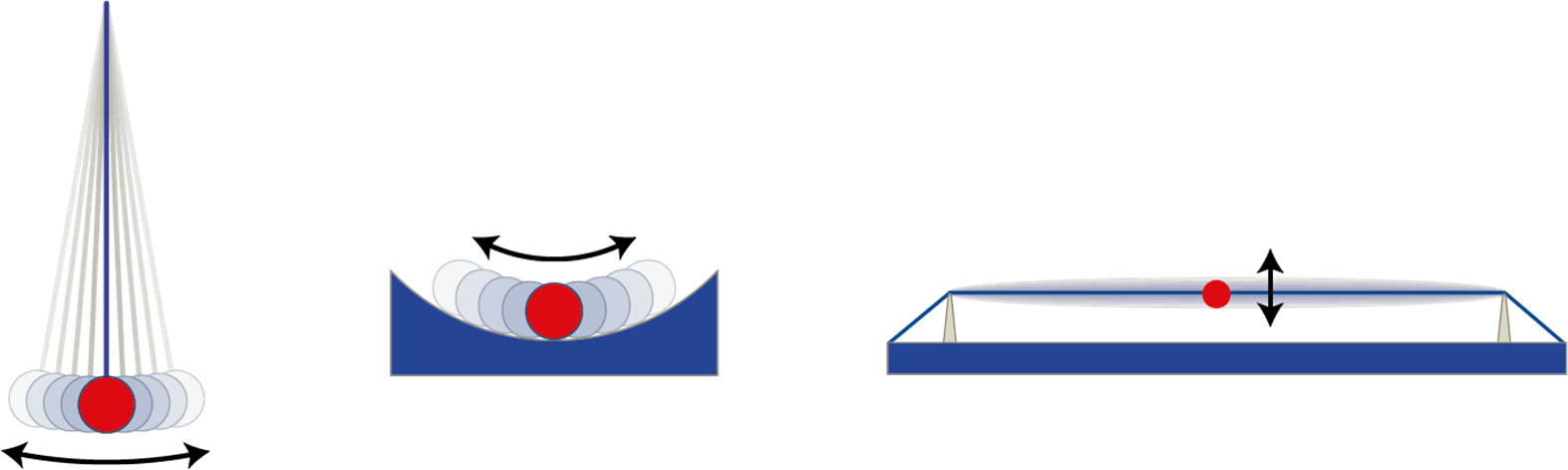
In tutti questi casi si ha un moto oscillatorio, che però non è necessariamente di tipo armonico (ad es. il pendolo semplice oscilla con moto armonico solo per piccole oscillazioni).

Tuttavia, se lo spostamento si mantiene sufficientemente piccolo, accade che la forza di richiamo è con ottima approssimazione proporzionale allo spostamento stesso. Pertanto, anche in tali casi (oltre che in quello paradigmatico massa-molla) si ha un moto armonico, purché l’ampiezza di oscillazione sia abbastanza piccola. Per quanto riguarda lo specifico caso del pendolo, questa proprietà era stata ben compresa da Galilei che quattro secoli fa mise in evidenza “l’isocronismo delle piccole oscillazioni”.