Il fissaidee

Cerchiamo di comprendere  come il comportamento macroscopico del gas possa essere spiegato da un modello microscopico con una breve introduzione a quella che si chiama “teoria cinetica” dei gas, originariamente sviluppata da James Clark Maxwell. 

Descriveremo un gas ideale come un sistema di palline che interagiscono solo con urti elastici e che hanno una dimensione molto minore della distanza media tra di esse. Di conseguenza, gli urti avvengono solo occasionalmente, mentre per la maggior parte del tempo le palline si muovono di moto uniforme in tutte le direzioni, naturalmente non tutte allo stesso modo ma con una certa distribuzione delle velocità. 

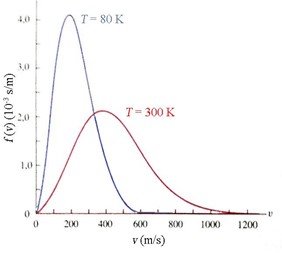
Maxwell, facendo pochissime assunzioni sulle proprietà che deve avere la distribuzione delle velocità all’equilibrio (ad esempio che non deve dipendere dalla direzione o dal verso della velocità stessa) riuscì a ottenerne l’andamento mostrato in figura, giustamente detto distribuzione maxwelliana. Al crescere della temperatura il picco si sposta verso valori più alti e si allarga. Quindi anche il valor medio di \( v \) (e pertanto l’energia cinetica media del gas) cresce con la temperatura. Per l’esattezza, Maxwell trovò che il valore medio dell’energia cinetica di un gas monoatomico costituito da \( N \) atomi gas vale: 

\( \overline E_c=\frac32Nk_B T \)

Se interpretiamo questa energia cinetica come energia interna \( U \) del gas, ne segue che la capacità termica di un gas monoatomico è pari a \( \frac 32Nk_B \), valore in ottimo accordo con i dati sperimentali. Tenendo conto dell’equazione di stato per i gas ideali (che viene pienamente giustificata dal modello di Maxwell), si ottiene infine 

\( PV=\frac 23 U \)

Successivamente Ludwig Boltzmann mostrò come un gas che parta da una condizione qualunque, anche molto lontana dall’equilibrio, raggiunge col tempo la distribuzione delle velocità trovata da Maxwell. Ciò avviene quando una certa grandezza, che dipende dalla funzione di distribuzione delle velocità, raggiunge il suo massimo valore. Questa grandezza è l’equivalente microscopico dell’entropia termodinamica ed il suo andamento giustifica, almeno in senso statistico, l’esistenza di una direzione del tempo.