Unit 2: indici di posizione (parte 1 di 3)
6. Determinazione della moda per dati raggruppati in classi /2
Consideriamo la distribuzione
delle frequenze relativa alle
altezze che abbiamo già visto in
precedenza:
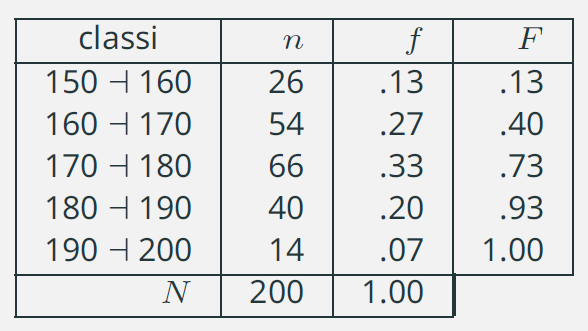
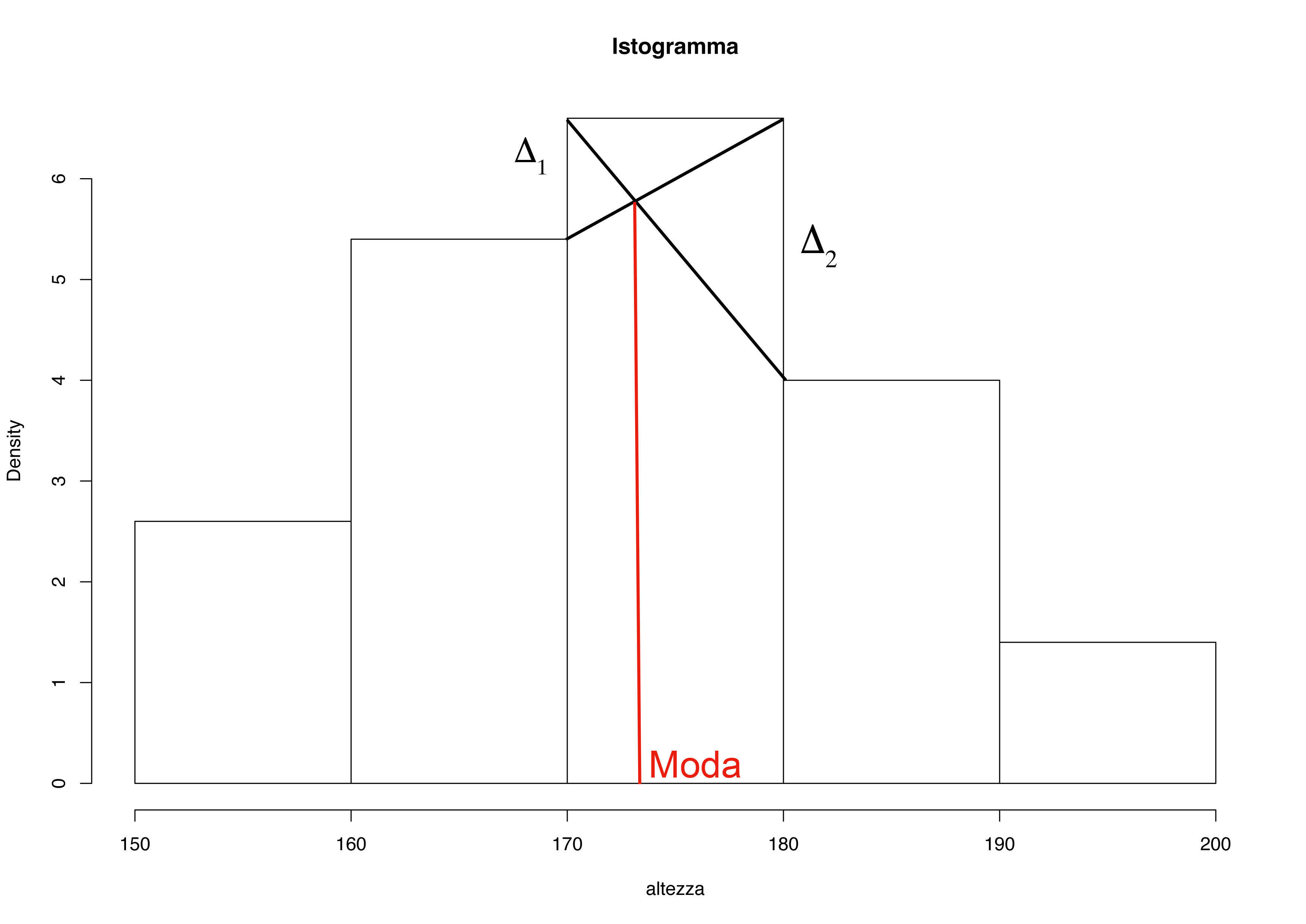
La classe \(170\) a \(180\) rappresenta la classe modale.
Indichiamo la moda con la notazione \(Mo\):
- regola della proporzione:
\[Mo = \inf (X_{Mo}) + a_{Mo} \dfrac{\Delta_1}{\Delta_1 + \Delta_2}\]
- dove \(\sup(X_{Mo})\) e \(\inf(X_{Mo})\) indicano rispettivamente il limite superiore e il limite inferiore della classe modale e \(a_{Mo} = \sup(X_{Mo}) − \inf(X_{Mo})\) è l’ampiezza della classe modale.
- Nell’esempio:
\[Mo = 170 + 10 \dfrac{12}{12 + 26} = 170 + 10 ∗ \dfrac{12}{38} = 173, 2\]