Unit 2: indici di posizione (parte 1 di 3)
| Sito: | Federica Web Learning - LMS |
| Corso: | Statistica Psicometrica |
| Unit: | Unit 2: indici di posizione (parte 1 di 3) |
| Stampato da: | Utente ospite |
| Data: | sabato, 21 febbraio 2026, 14:06 |
Descrizione
- Sintesi di una distribuzione univariata
- Le medie: definizione
- La moda: definizioni, criteri di calcolo e proprietà
1. Riassumere la distribuzione
Indici
Le distribuzioni che abbiamo osservato sono diverse fra loro in virtù di una o più
caratteristiche.
La statistica descrittiva descrive le distribuzioni sulla base di indici:
- Tendenza centrale
- Variabilità
- Forma
- Asimmetria
- Curtosi
2. Le medie /1
- Osservando le distribuzioni di frequenza e gli istogrammi si può avere un’idea (approssimativa) della magnitudine (o ordine di grandezza) della variabile che è stata osservata.
- Le misure di tendenza centrale, dette anche medie, permettono di individuare una modalità che sia rappresentativa dell’intera distribuzione e che sia quindi in grado di offrire una misura più o meno rappresentativa dell’ordine di grandezza della variabile osservata.
- Da un punto di vista grafico, pensando all’istogramma, la tendenza centrale si può interpretare come il punto di ancoraggio della distribuzione rispetto all’asse della ascisse, che rappresenta il supporto della variabile.
- Esistono molte misure di tendenza centrale (o medie). Ciascuna media gode di specifiche proprietà in base alle quali siamo in grado di interpretarne il significato, di capire in che modo cattura la magnitudine della variabile osservata.

Corrado Gini, Le medie, (1958), UTET, Torino
3. Le medie /2
Definizione generale di media
“Noi siamo così arrivati, per le medie, a formulare che valgono per un numero qualunque di termini (pari o dispari), comunque disposti, subordinatamente alla condizione che il risultato sia intermedio fra i termini
estremi” (C. Gini, Le medie (1958), UTET, Torino)
- L’internalità è condizione necessaria ma anche sufficiente per assumere che una “media di più quantità è una nuova quantità compresa tra la più piccola e la più grande di quelle prese in considerazione”.
- In parole semplici, data una generica serie
\[X : x_1, x_2, \dots , x_N ,\]
che per comodità assumiamo ordinata, qualsiasi funzione \(f(X)\) tale che:
\[ x_1 \leq f(x_1, x_2, \dots , x_N ) \leq x_n , \]è una media.
4. Tendenza centrale: medie di posizione
Le medie di posizione individuano una particolare modalità in base alla posizione che essa occupa nella serie ordinata.
La moda
Si definisce moda la modalità che si presenta con la frequenza massima. Per
individuare la moda bisogna raggruppare le modalità in classi omogenee, la classe
più numerosa prende il nome di classe modalea
.
Nel caso di caratteri qualitativi (nominali o ordinali) la moda coincide con la modalità
che si presenta con la frequenza più alta.
Nel caso delle variabili continue si procede come segue:
- si identifica la classe modale, quella che si presenta con la frequenza più alta;
- all’interno della classe modale si identifica una sola modalità scegliendo il valore centrale della classe oppure si procede utilizzando una proporzione.
aLa moda è detta anche norma.
5. Determinazione della moda per dati raggruppati in classi /1
Consideriamo la distribuzione delle frequenze relativa alle altezze che abbiamo già visto in precedenza:
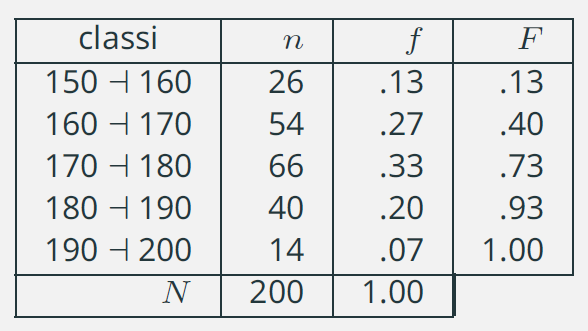
La classe \(170\) a \(180\) rappresenta la classe modale. Indichiamo la moda con la notazione \(Mo\):
- regola del valore centrale della classe:
- dove \(\sup(X_{Mo})\) e \(\inf(X_{Mo})\) indicano rispettivamente il limite superiore e il limite inferiore della classe modale.
\[Mo = \dfrac{\sup(X_{Mo}) + \inf(X_{Mo})}{2}\]
- Nell’esempio:
\[Mo = \dfrac{180 + 170}{2} = 175\]
6. Determinazione della moda per dati raggruppati in classi /2
Consideriamo la distribuzione
delle frequenze relativa alle
altezze che abbiamo già visto in
precedenza:
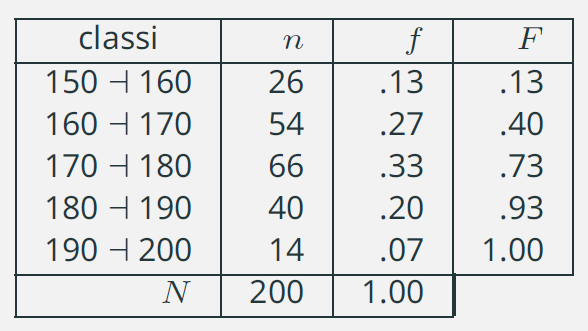
La classe \(170\) a \(180\) rappresenta la classe modale.
Indichiamo la moda con la notazione \(Mo\):
- regola della proporzione:
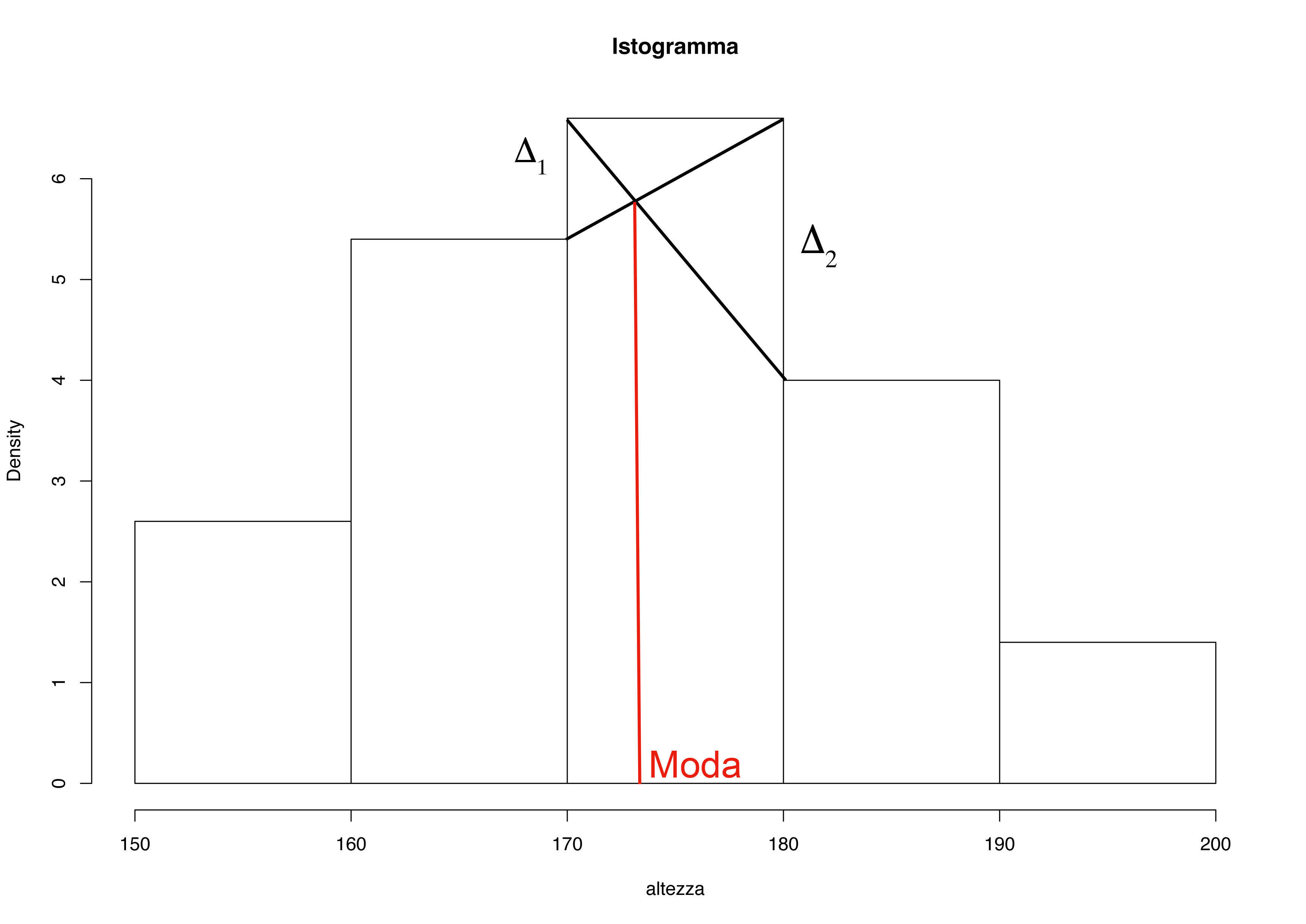
\[Mo = \inf (X_{Mo}) + a_{Mo} \dfrac{\Delta_1}{\Delta_1 + \Delta_2}\]
- dove \(\sup(X_{Mo})\) e \(\inf(X_{Mo})\) indicano rispettivamente il limite superiore e il limite inferiore della classe modale e \(a_{Mo} = \sup(X_{Mo}) − \inf(X_{Mo})\) è l’ampiezza della classe modale.
- Nell’esempio:
\[Mo = 170 + 10 \dfrac{12}{12 + 26} = 170 + 10 ∗ \dfrac{12}{38} = 173, 2\]
7. Centralità della moda
Per dare un significato agli indici di tendenza centrale bisogna comprende e interpretare la loro centralità all’interno della distribuzione.
La moda è il centro di ordine 0
Avendo definito la moda come la modalità che si presenta con la frequenza più alta all’interno
della distribuzione e ricordando che qualsiasi numero diverso da \(0\) elevato a \(0\) è uguale ad \(1\),
possiamo facilmente verificare che:
\[\sum_{i=1}^N = (x_i − Mo)^0 = \min , \]
la somma degli scarti alla potenza \(0\) rispetto ad un indice di tendenza centrale \(M\) è minima se e solo se l’indice a cui si fa riferimento è la moda.
Tipi di carattere per cui è possibile determinare la moda.
La determinazione della moda richiede l’utilizzo del solo operatore logico \(= / \neq\) e il risultato è
necessariamente una modalità osservata o appartenente al dominio di definizione e pertanto
la moda può essere definita per qualsiasi tipologia di carattere.