Unit 3: indici di posizione (parte 2 di 3)
| Sito: | Federica Web Learning - LMS |
| Corso: | Statistica Psicometrica |
| Unit: | Unit 3: indici di posizione (parte 2 di 3) |
| Stampato da: | Utente ospite |
| Data: | sabato, 28 febbraio 2026, 04:26 |
Descrizione
- Medie di posizione
- La mediana: definizione, criteri di calcolo e proprietà
- Quartili di una distribuzione
- Quantili di una distribuzione
Indice Unit
- 1. Tendenza centrale: medie di posizione /1
- 2. Tendenza centrale: medie di posizione /2
- 3. Determinazione della mediana per dati raggruppati in classi
- 4. Mediana per dati raggruppati in classi: interpolazione /1
- 5. Mediana per dati raggruppati in classi: interpolazione /2
- 6. Centralità della mediana
- 7. Quartili della distribuzione
- 8. Quantili della distribuzione
1. Tendenza centrale: medie di posizione /1
La mediana
Si definisce mediana la modalità che presenta l’unità statistica che occupa la posizione centrale nelle serie ordinata.
- si ordinano le modalità in modo crescente;
- si individua la posizione centrale;
- la modalità dell’unità statistica che occupa la posizione centrale è la mediana.
Nel caso di caratteri ordinali la mediana corrisponde necessariamente ad una modalità osservata. Nel caso di variabili continue con modalità raggruppate in classi:
- si identifica la classe mediana, quella che contiene l’unità centrale;
- all’interno della classe mediana si identifica una sola modalità utilizzando la regola della proporzione.
2. Tendenza centrale: medie di posizione /2
Illustriamo con un esempio molto semplice la procedura per la individuazione della mediana.
- Consideriamo la serie ordinata
\[ 0, 1, 3, 5, 6 \]
di lunghezza \( N = 5 \) (dispari!) e indichiamo con \( X_{Me} \) la posizione centrale (mediana), per determinare \( X_{Me} \) si procede come segue:
\[ X_{Me} = \dfrac{N+1}{2} = \dfrac{5+1}{2} = 3 \]
L’unità statistica che occupa la posizione \( X_{Me} = 3 \) nella serie corrisponde alla modalità 3, quindi \( Me = 3 \).
- Consideriamo adesso la serie \(0, 1, 3, 5, {\bf 10} \). La serie è cambiata solo per una modalità estrema, ma la mediana resta sempre uguale a \(Me = 3\).
- Osservare che se la serie è di lunghezza pari (\(N\) è pari) non ci sarà una unità centrale. Se il carattere considerato lo permette, possiamo considerare come mediana la semisomma delle modalità centrali.
3. Determinazione della mediana per dati raggruppati in classi
Consideriamo la distribuzione delle frequenze relativa alle altezze che abbiamo già visto in precedenza.
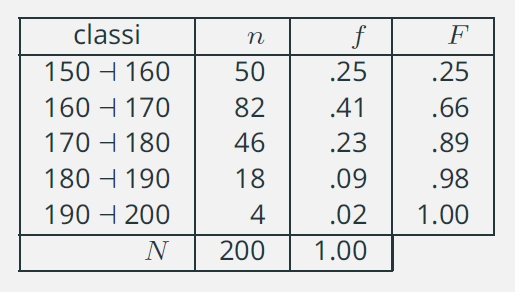
La classe 160 a 170 rappresenta la classe mediana, è la classe che contiene le unità 100 e 101 della serie ordinata (N è pari!).
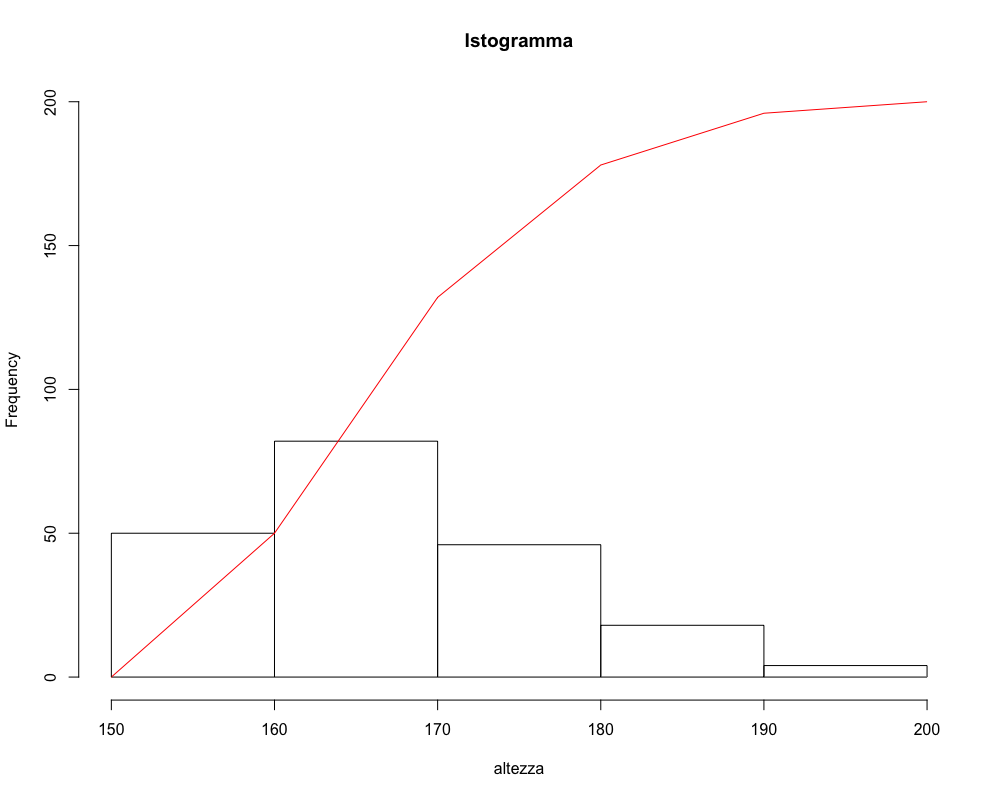
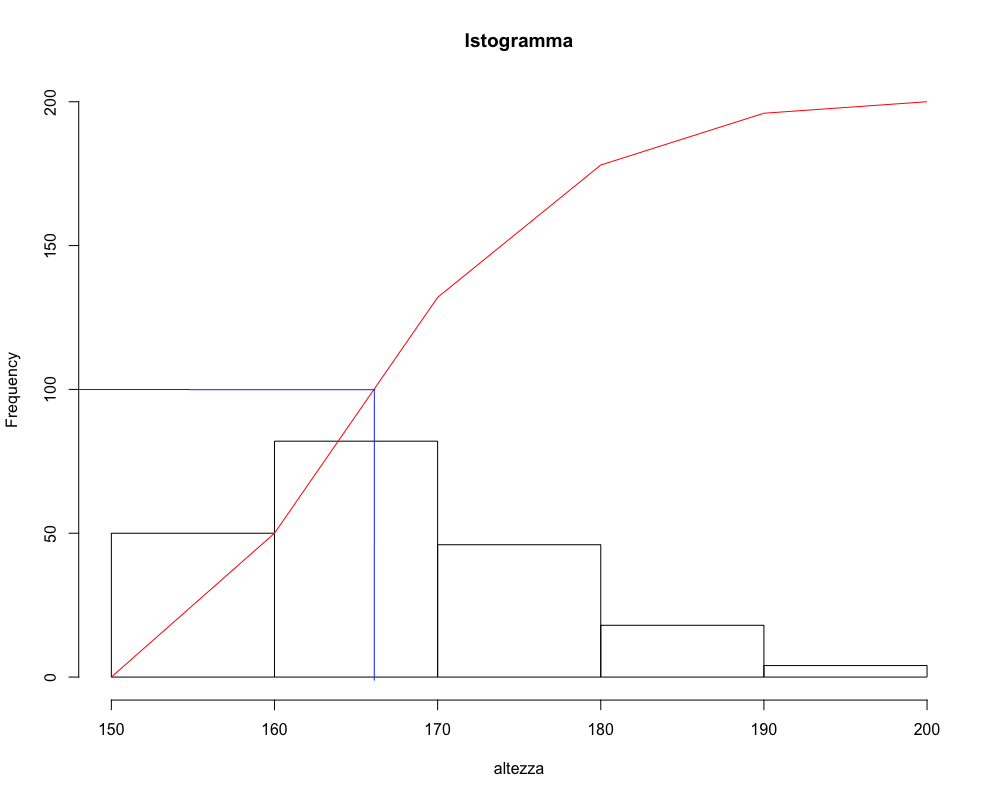
Per determinare la media occorre disegnare il diagramma di Pareto, che sovrappone in un solo grafico la distribuzione delle frequenze e la funzione di ripartizione.
Individuando il centro della distribuzione sull’asse delle ordinate e proiettando la sua tale ordinata della funzione di ripartizione sull’asse delle ascisse è possibile individuare la mediana. Questa procedura è detta metodo grafico per il calcolo della mediana.
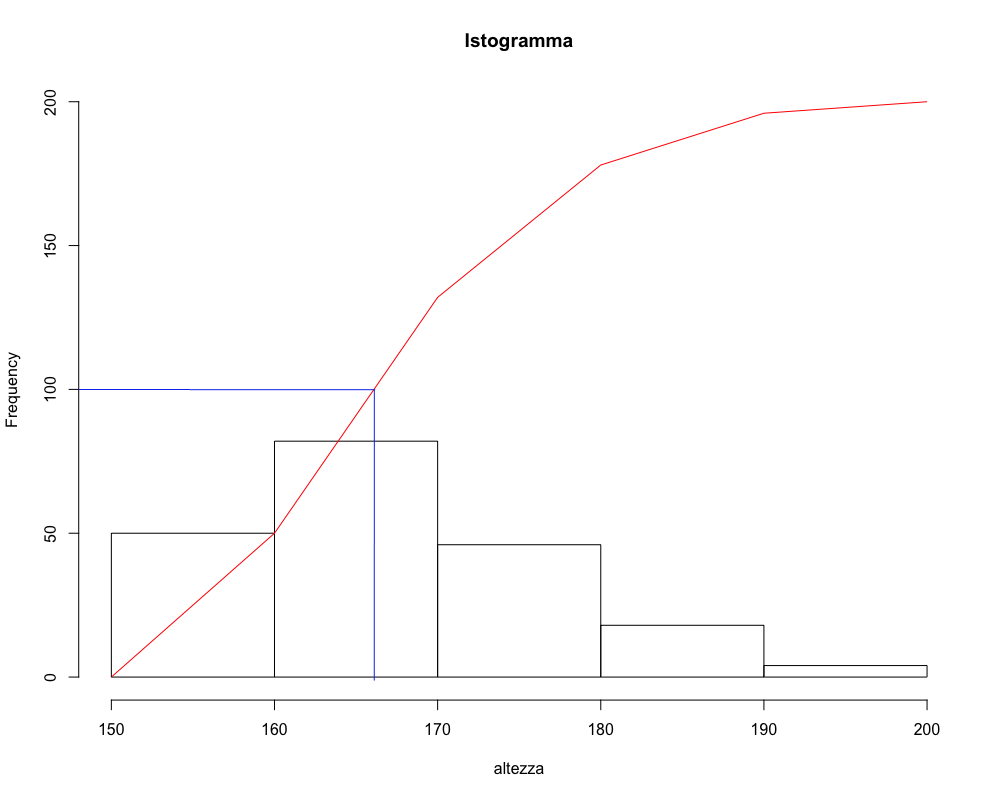
4. Mediana per dati raggruppati in classi: interpolazione /1
Consideriamo la distribuzione delle frequenze relativa alle altezze che abbiamo già visto in precedenza.
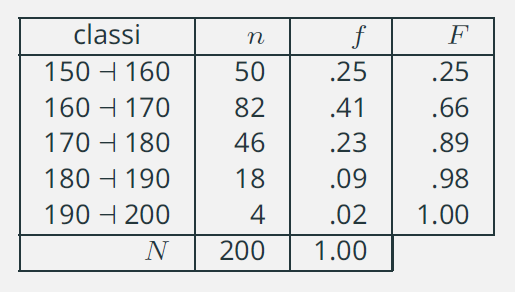
La classe \(160\) a \(170\) rappresenta la classe mediana.
Indichiamo la classe mediana con \(X_{Me}\) e la mediana con \(Me\):
- regola della proporzione:
\[ Me = \inf (X_{Me}) + a_{Me} \dfrac{F(X_{Me}) − F(X_{Me^{-}})}{f(X_{Me})} \]
- la mediana corrisponde alla modalità individuata come il limite inferiore della classe mediana più una frazione dell’ampiezza, proporzionale alla frequenza fra \( F(X) = 0,5 = \dfrac{N}{2} \) meno il retrocumulo e la frequenza della classe mediana.
- - Nell’esempio:
\[ Me = 160 + 10 \dfrac{0,50 − 0,25}{0,41}= 166,1 \]
5. Mediana per dati raggruppati in classi: interpolazione /2
Rivediamo in dettaglio:
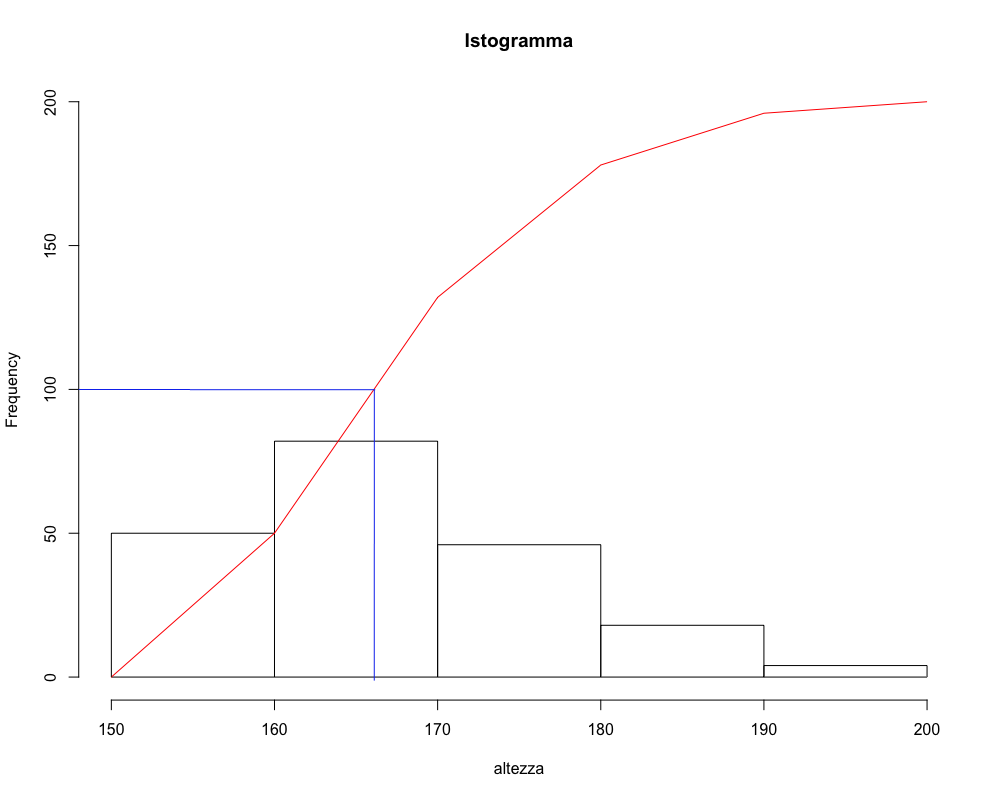
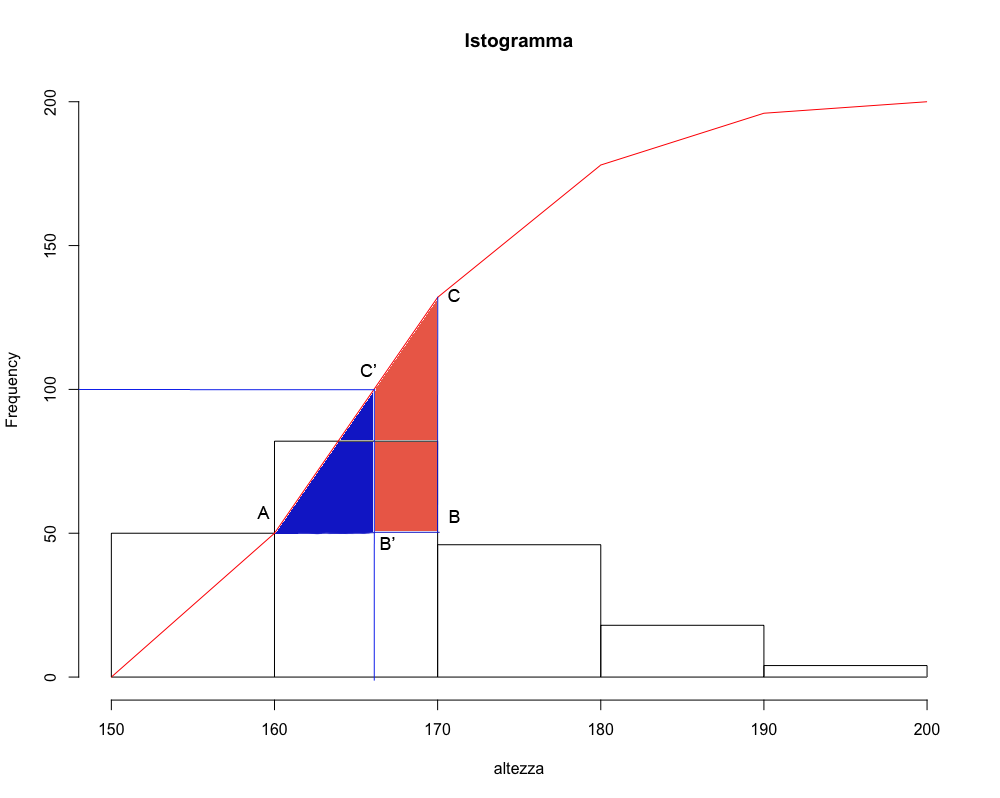
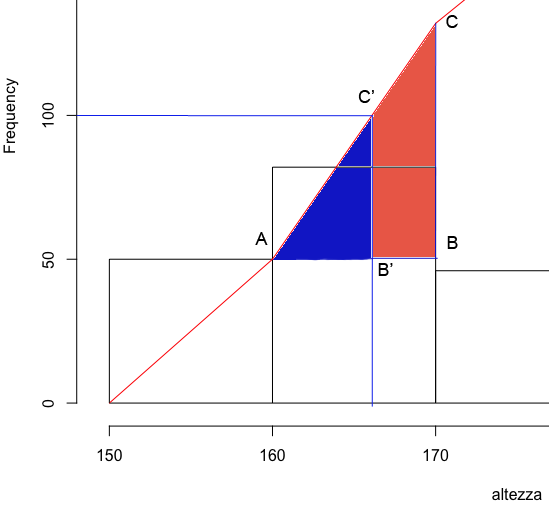
I triangoli \(ABC\) e \(AB'C'\) sono simili, quindi la quantità che interessa calcolare \(AB'\) può essere ricavata dalla proporzione:
\[ AB' : AB = C'B' : CB \]
6. Centralità della mediana
Per dare un significato agli indici di tendenza centrale bisogna comprende e interpretare la loro centralità all’interno della distribuzione.
La mediana è il centro di ordine 1
Avendo definito la mediana come la modalità che occupa la posizione centrale della serie ordinata, si avrà che:
\[ \sum_{i=1}^N| x_i − Me | = \min ,\]
la somma degli scarti in valore assoluto rispetto ad un indice di tendenza centrale \(M\) è minima se e solo se l’indice a cui si fa riferimento è la mediana.
Tipi di carattere per cui è possibile determinare la mediana.
La determinazione della mediana richiede l’utilizzo dei soli operatori logici (\( \bf = / \neq \) e \( \bf < / > \)) e il
risultato è necessariamente una modalità osservata o appartenente al dominio di definizione e pertanto la mediana può essere definita per qualsiasi tipologia di carattere ordinabile.
7. Quartili della distribuzione
Utilizzando un principio del tutto analogo a quello visto per la mediana si possono determinare altri modalità notevoli che corrispondono a specifici livelli della funzione di ripartizione.
Quartili: Si definiscono quartili le modalità che dividono in quattro parti uguali la serie ordinata.
\(Q_1\) Il primo quartile divide la distribuzione (la serie ordinata) in due parti non uguali: \(25\%\) prima e \(75\%\) dopo.
\(Q_2\) Il secondo quartile coincide con la mediana e divide la distribuzione (la serie ordinata) in due parti uguali.
\(Q_3\) Il terzo quartile divide la distribuzione (la serie ordinata) in due parti uguali non uguali: \(75\%\) prima e \(25\%\) dopo.
Con lo stesso principio si può ripartire la distribuzione in dieci parti uguali attraverso i decili o in cento parti uguali individuando i percentili. È possibile suddividere una distribuzione in un qualsiasi punto utilizzando il generico quantile.
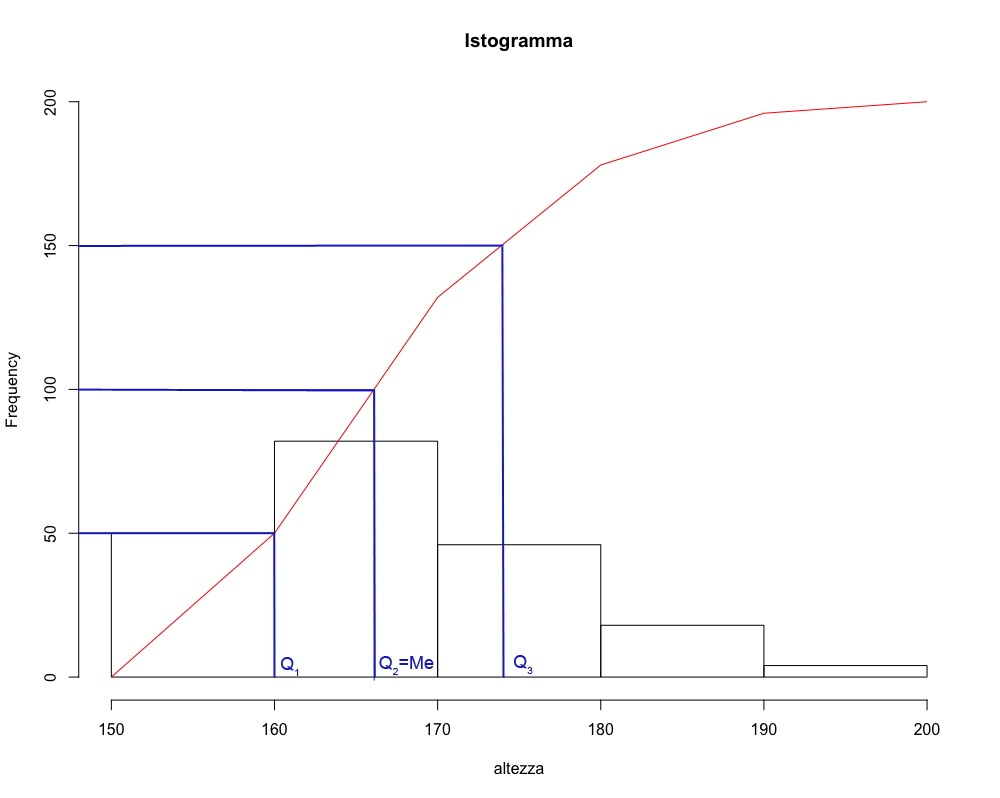
8. Quantili della distribuzione
Dati raggruppati in classi
Se il carattere è rappresentato da una variabile continua le cui modalità sono state raggruppate in classi, per la determinazione dei quartili si può ricorrere alla formula calcolo già vista per la mediana.
\[ Q_1 = \inf(Q_1) + a_{Q_1}\dfrac{0,25 - F(X_{Q_1^{-}})}{f(X_{Q_1})} \]
\[ Q_3 = \inf(Q_3) + a_{Q_3}\dfrac{0,75 - F(X_{Q_3^{-}})}{f(X_{Q_3})} \]
Determinazione dell’ottantesimo percentile: \(P_{80}\)
\[ P_{80} = \inf(P_{80}) + a_{P_{80}}\dfrac{0,80 - F(X_{P_{80}^{-}})}{f(X_{P_{80}})} \]