Unit 1: frequenze, distribuzioni di frequenze ed istogrammi
| Sito: | Federica Web Learning - LMS |
| Corso: | Statistica Psicometrica |
| Unit: | Unit 1: frequenze, distribuzioni di frequenze ed istogrammi |
| Stampato da: | Utente ospite |
| Data: | sabato, 21 febbraio 2026, 15:38 |
Descrizione
- Distribuzioni di frequenza per classi
- Istogramma
1. Distribuzione delle frequenze
Quando la numerosità del collettivo diventa grande, le modalità osservate sono troppo numerose perché da una semplice osservazione si possa apprezzare come si è distribuito il carattere all’interno del collettivo.
Tabelle che associano a ciascuna modalità la frequenza corrispondente sono denominate distribuzioni di frequenza.
Nel caso di caratteri quantitativi è necessario, per ottenere la distribuzione di frequenza, creare classi di modalità.
| Classi | n | f | I | ||
|---|---|---|---|---|---|
| 0 | - | 2,0 | 4 | 0,114 | 0,057 |
| 2,0 | - | 2,5 | 6 | 0,171 | 0,343 |
| 2,5 | - | 3,0 | 15 | 0,429 | 0,857 |
| 3,0 | - | 5,0 | 9 | 0,257 | 0,129 |
| 5,0 | - | 8,0 | 1 | 0,029 | 0,010 |
| Totale | 35 | 1,000 | |||
- Per ottenere una distribuzione di frequenza a partire da un carattere continuo è necessario suddividere il campo di variazione del carattere in Classi. Le classi possono essere di eguale ampiezza (tabella a sinistra) o di ampiezza variabile (a destra).
- Per creare le classi è necessario suddividere l’intervallo in cui è definito il carattere in sottointervalli di eguale ampiezza (classi equiampie) o di ampiezza differente.
- Utilizzare classi di ampiezza differente è utile soprattutto nel caso di distribuzioni caratterizzate da forte asimmetria o con forte variabilità verso i valori estremi
- Il simbolo “\(\dashv\) indica che l’estremo inferiore della classe è incluso e l’estremo superiore è escluso.
- Le frequenze assolute, generalmente indicate con \(n\), per ciascuna classe, indicano il numero delle unità statistiche che presentano una modalità appartenente all’intervallo della classe.
La somma di tutte le frequenze assolute corrisponde alla numerosità del collettivo, che generalmente si indica con \(N\). - Le frequenze relative si determinano dividendo le frequenze assolute per il la frequenza totale: \[f = \frac{n}{N}.\]
Il totale delle frequenze relative, naturalmente, è sempre 1. - L’intensità si utilizza per realizzare istogrammi con classi di ampiezza differente e si determina dividendo la frequenza relativa per l’ampiezza della classe: \[I = \frac{f}{{\rm sup}(x) - {\rm inf}(x)}.\]
- Per rappresentare graficamente la distribuzione delle frequenze associate a un carattere continuo o variabile si utilizza l’istogramma.
- L’istogramma è costituito da una serie di rettangoli contigui, che hanno per base l’ampiezza della classe e la superficie proporzionale alla frequenza della classe. Utilizzando questo principio è possibile accorpare due o più classi contigue o definire distribuzioni in classi che hanno ampiezze diverse.
- L’istogramma è una
rappresentazione della distribuzione delle frequenze su un piano
cartesiano (generalmente) l’asse delle ascisse rappresenta il carattere e
le ordinate le altezze dei rettangoli determinate dal rapporto fra
l’area e l’ampiezza della
base.
---------------------------------------------------------------
Ecco due esempi ricavati a partire dalla serie completa della variabile
| Classi | n | f | I | ||
|---|---|---|---|---|---|
| 1,0 | - | 3,0 | 25 | 0,714 | 0,357 |
| 3,0 | - | 5,0 | 9 | 0,257 | 0,129 |
| 5,0 | - | 7,0 | 0 | 0,000 | 0,000 |
| 7,0 | - | 9,0 | 1 | 0,029 | 0,014 |
| Totale | 35 | ||||
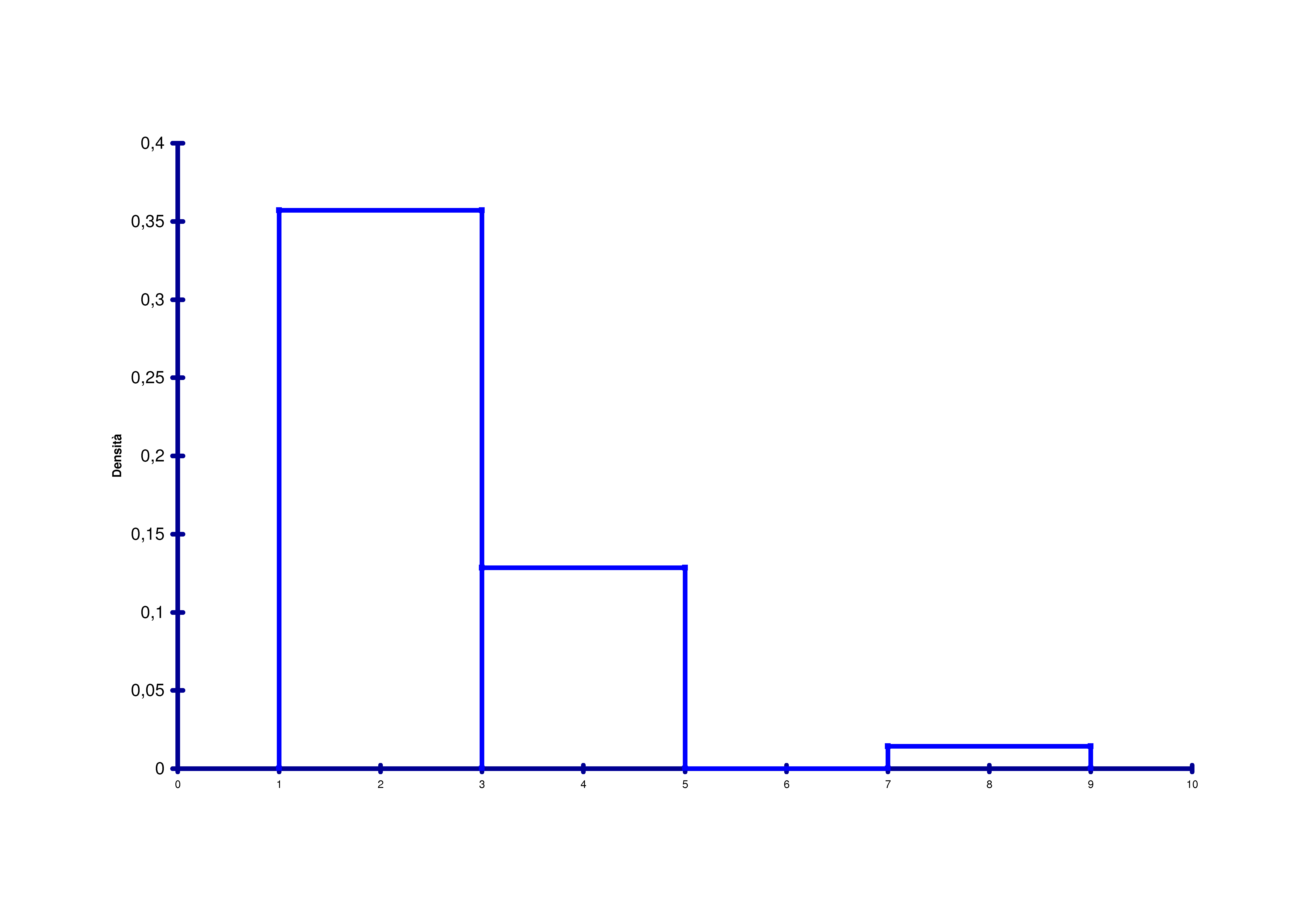
Distribuzione delle frequenze e istogramma con classi di ampiezza uguale.
Nel grafico la scala delle ordinate riporta le intensità.
| Classi | n | f | I | ||
|---|---|---|---|---|---|
| 0 | - | 2,0 | 4 | 0,114 | 0,057 |
| 2,0 | - | 2,5 | 6 | 0,171 | 0,343 |
| 2,5 | - | 3,0 | 15 | 0,429 | 0,857 |
| 3,0 | - | 5,0 | 9 | 0,257 | 0,129 |
| 5,0 | - | 8,0 | 1 | 0,029 | 0,010 |
| Totale | 35 | 1,000 | |||
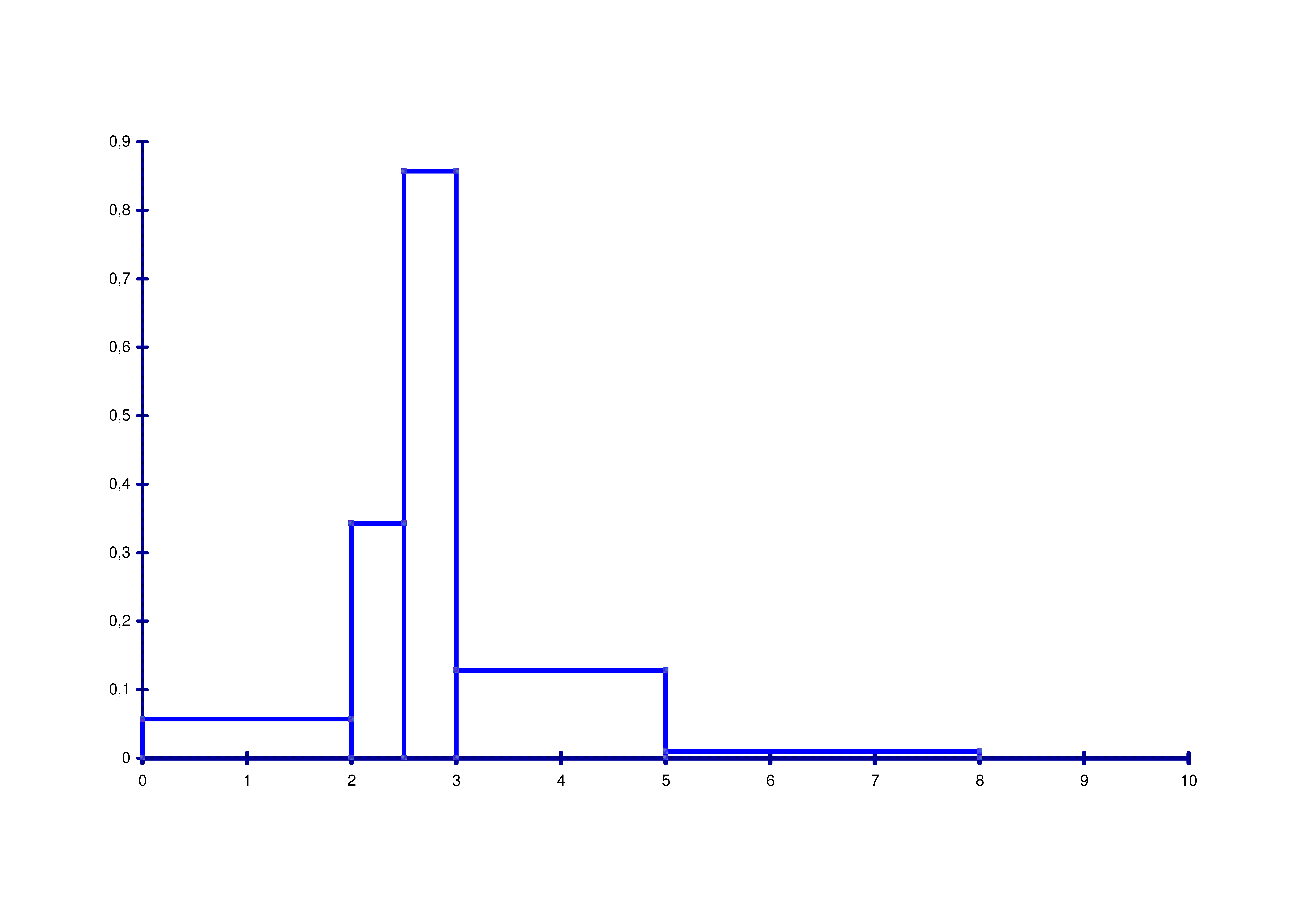
Distribuzione delle frequenze e istogramma con classi di ampiezza diversa.
Nel grafico la scala delle ordinate riporta le intensità.
-------------------------------------------------
Dal confronto dei due istogrammi appare evidente che in questo caso è preferibile adottare classi di ampiezze differenti
2. Distribuzione delle frequenze per una variabile
Notazione
- frequenza assoluta \(\{n_1, n_2, \cdots, n_k\} \longrightarrow\) numero di unità statistiche che appartengono alla classe
- numerosità del collettivo \(N\)
- frequenza relativa \(\{f_1, f_2, \cdots, f_k\}\longrightarrow\) \(f_i = n_i/N\) per \(i=1,\ldots k\)
- frequenza (relativa) cumulata \(\{F_1, F_2, \cdots, F_k\}\longrightarrow\) \(F_1=f_1, \quad F_2 = f_1 + f_2,\) ecc.
3. Istogramma - classi di eguale ampiezza
- Per rappresentare graficamente la distribuzione delle frequenze associate a un carattere continuo o variabile si utilizza l'istogramma.
- L’istogramma è una rappresentazione della distribuzione delle frequenze su un piano cartesiano, (generalmente) l’asse delle ascisse rappresenta il carattere e le ordinate le altezze dei rettangoli, determinate dal rapporto fra l’area e l’ampiezza della
base.
- L’istogramma è costituito da una serie di rettangoli contigui, che hanno per base l’ampiezza della classe e la superficie proporzionale alla frequenza della classe. Utilizzando questo principio è possibile accorpare due o più classi contigue o definire distribuzioni in classi che hanno ampiezze diverse.
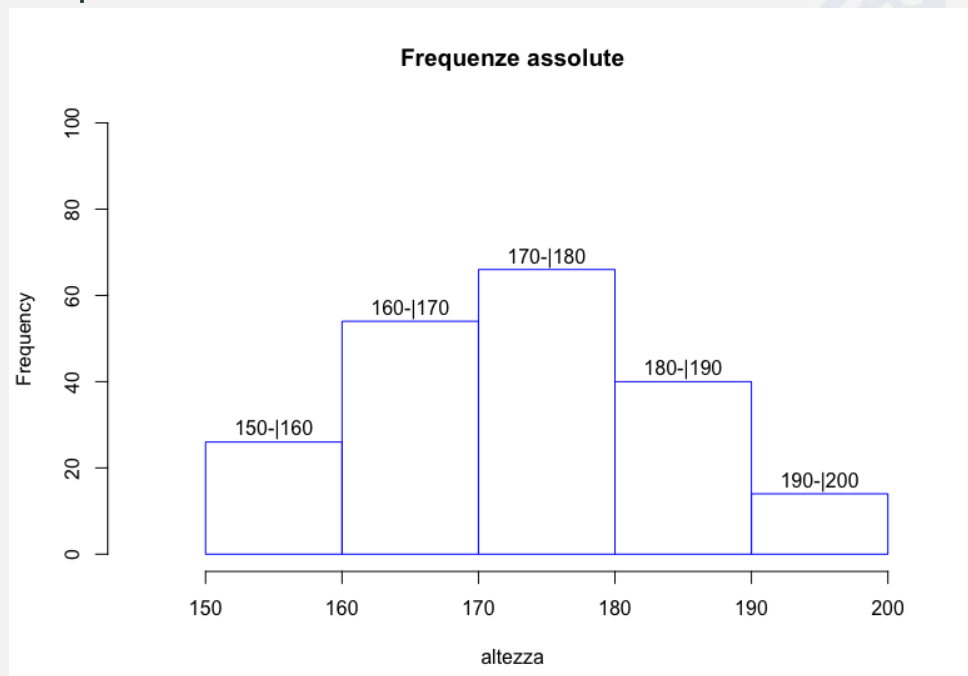
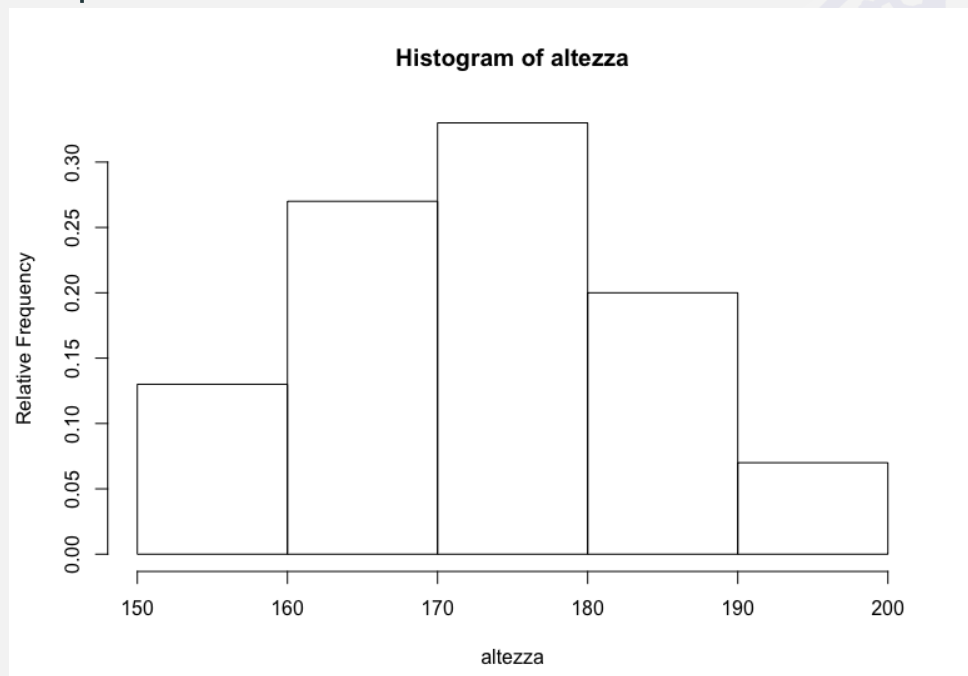
4. Istogramma - classi di ampiezza diversa
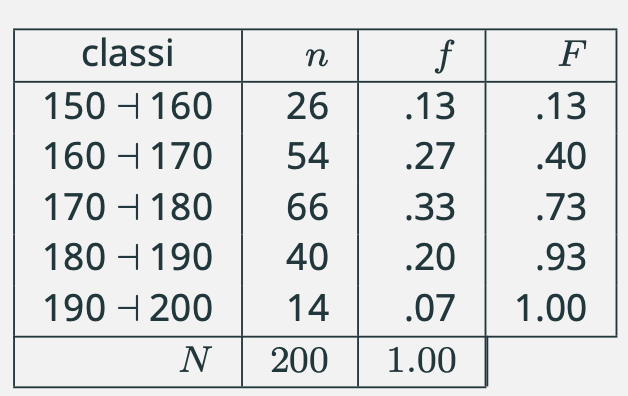
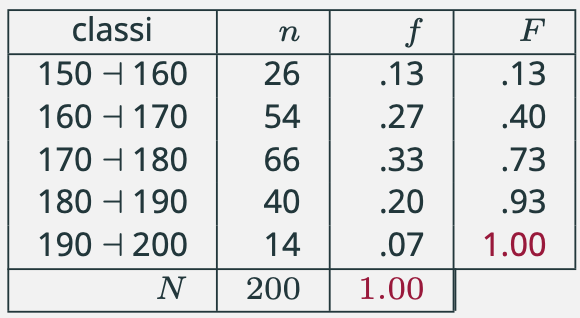
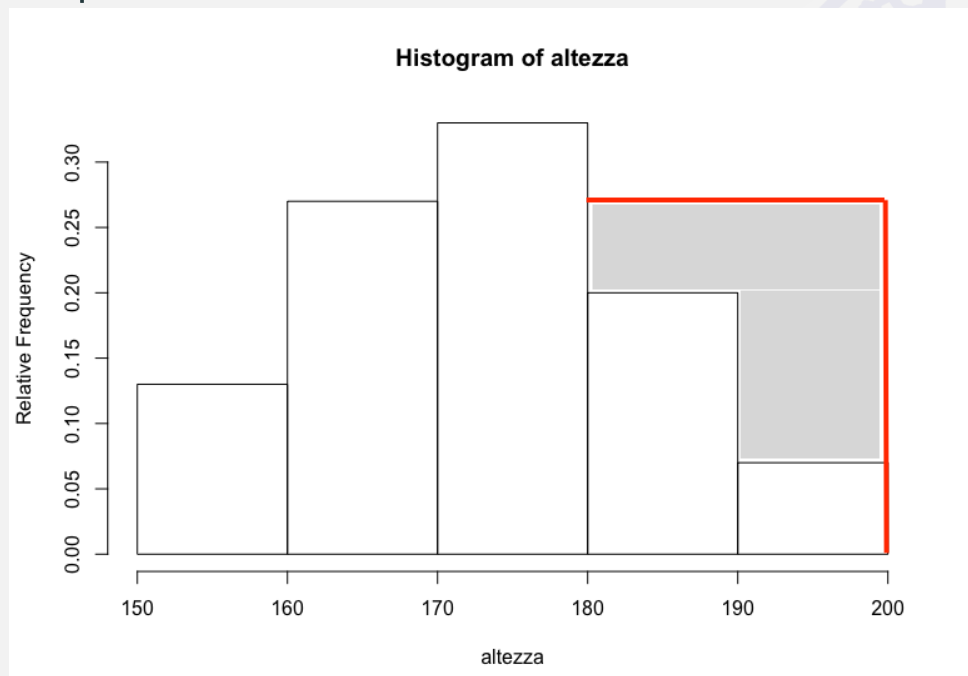
Consideriamo sempre gli stessi dati, ma le ultime due classi \([180 \dashv 190]\) e \([190 \dashv 200]\) sono state raggruppate in un’unica classe \([180 \dashv 200]\).
Raggruppando due classi, o comunque fissando classi di ampiezza differente, non è possibile continuare a utilizzare la frequenza (assoluta o relativa) per determinare l’altezza dei rettangoli. Per preservare il rapporto fra area del rettangolo e frequenza della classe bisogna ricorrere alle intensità (o densità).
La tabella che segue riporta la distribuzione in cui le ultime due classi sono state riunite in un'unica classe.
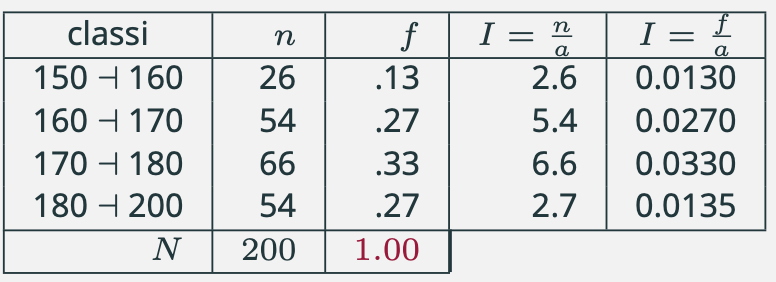
La rappresentazione per mezzo delle intensità (densità) è l’unica possibile se le classi non sono equiampie.
Le intensità si ricavano dalla formula \[I_i = \frac{n_i}{a_i}\], dove \(a_i\) indica l’ampiezza della classe e, per ciascuna classe è calcolata attraverso la differenza fra l’estremo superiore e l’estremo inferiore della classe stessa.
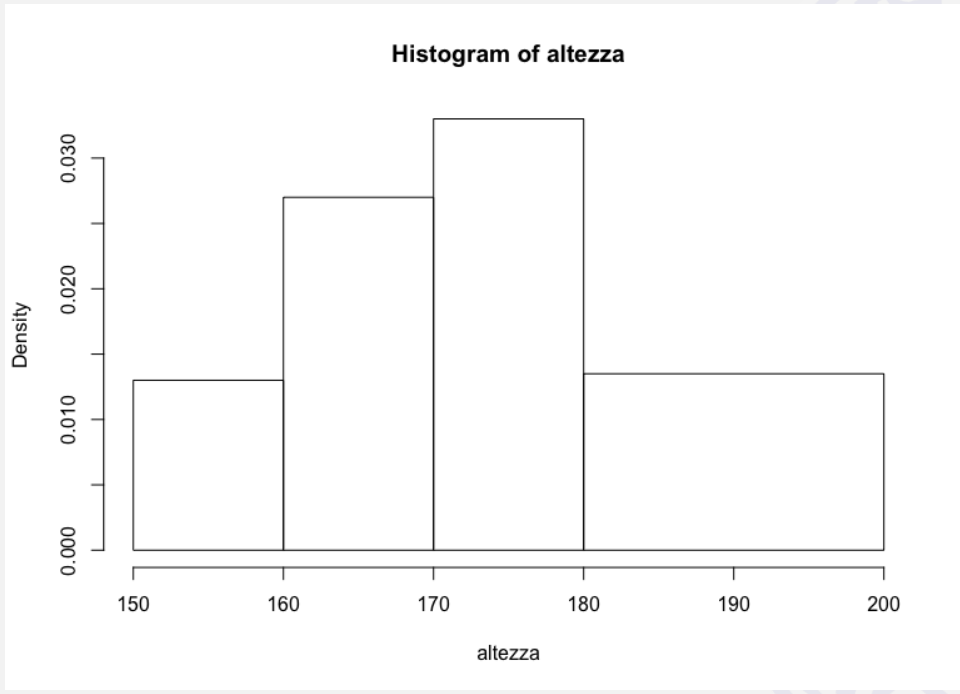
Poiché l'area descritta da ciascun rettangolo e quindi anche l'area totale dell'istogramma devono essere in proporzione alla frequenza che rappresentano e questa proporzione resta costante, se si utilizzasse la frequenza e non l'intensità si avrebbe una rappresentazione come quella riportata di seguito, dove l'area grigia rappresenta un accrescimento ingiustificato dell'area totale. Ingiustificato poiché non corrisponde a un incremento della frequenza, ma solo a una sua diversa distribuzione fra le classi.
5. Istogramma - classi di ampiezza diversa/2
Proponiamo un altro esempio con gli stessi dati, ma con diverso raggruppamento delle modalità in classi. Il principio resta lo stesso.
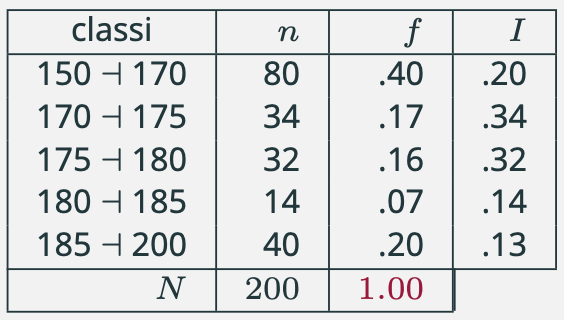
E questo è l'istogramma basato sulle intensità (colonna I) corrispondente.
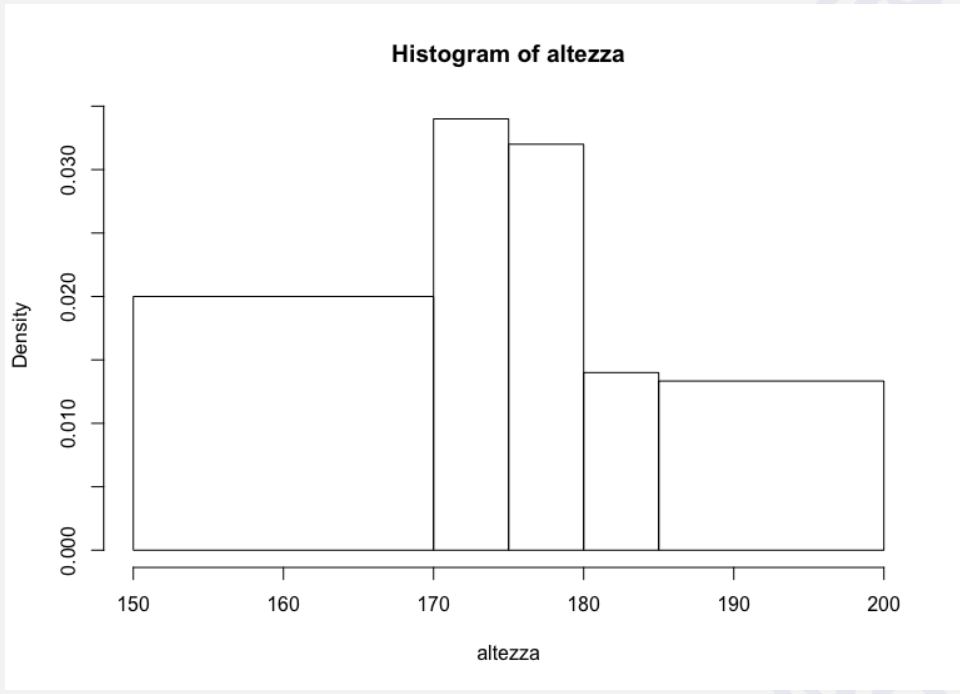
6. Istogramma - caratteristiche
- Assumiamo di aver registrato il generico carattere \(X\) su un collettivo di \(N = 1000\) unità statistiche, tale che \( X = x_1, x_2, \dots , x_N \) .
- Raggruppando le modalità in classi, e costruendo la corrispondente tabella della distribuzione distribuzione di frequenze si ottiene una rappresentazione della serie che offre utili indicazioni su come il carattere si distribuisce all’interno del collettivo.
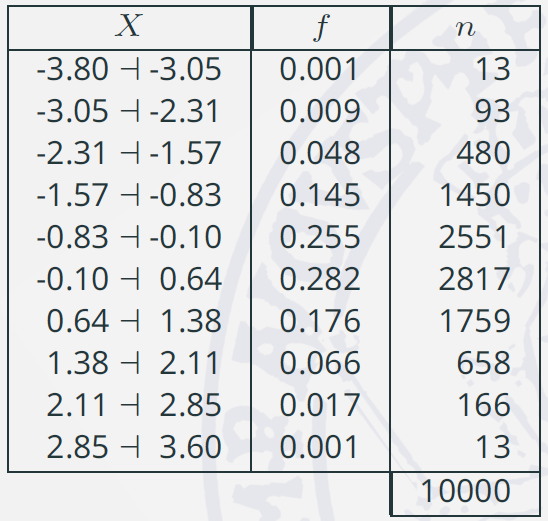
- L’istogramma corrispondente può essere di più semplice interpretazione.
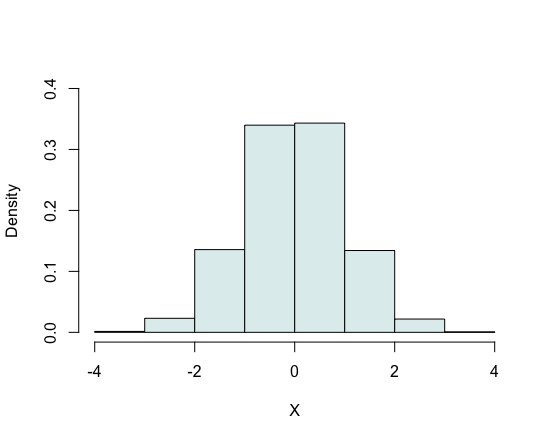
La figura seguente ci mostra come un istogramma può modificarsi.
Osservando la sequenza delle figure osserviamo tre tipi principali di modificazioni:
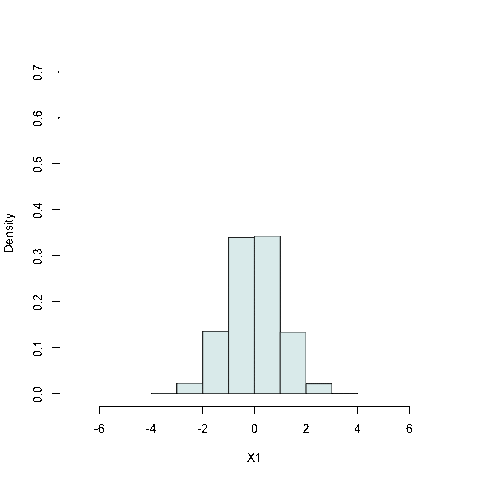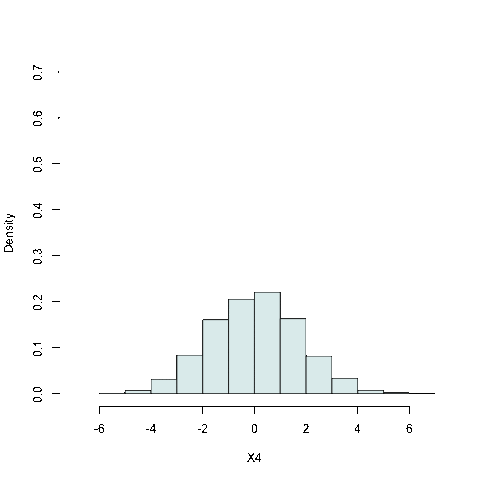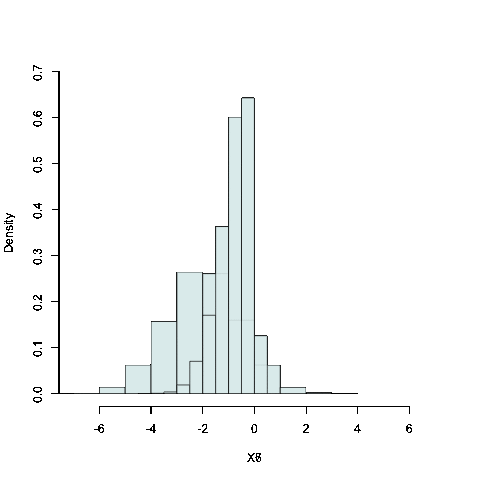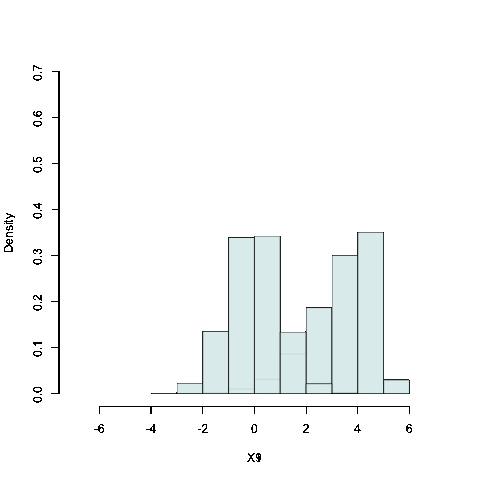
a) l'stogramma trasla lungo l'asse delle \(X\)
b) la frequenza delle classi tende a essere più o meno concentrata su una certa modalità
c) l'istogramma ha un asse di simmetria
Per valutare in termini quantitativi, utilizzando opportuni indici statistici, le differenze che caratterizzano questi diversi istogrammi bisogna, in primo luogo, dare una definizione per ciascuna alterazione e successivamente individuare una classe di indici o misure che la possano descrivere.
Le tre caratteristiche possono essere riconducibili ai tre seguenti aspetti
a) indici che utili a determinare una modalità che possa dare una indicazione relativa alla posizione della distribuzione rispetto all'asse delle ascisse vengono detti indici di tendenza centrale.
b) l'attitudine del carattere a variare all'interno del collettivo di riferimento indica la variabilità di una variabile.
c) la presenza di un asse di simmetria definisce l'asimmetria della distribuzione e rientra nella valutazione delle forma della distribuzione.d) oltre alla asimmetria della distribuzione esiste anche un altro aspetto che caratterizza la forma della distribuzione, che prende il nome di curtosi. Curtosi o ingobbimento si riferiscono al rapporto fra la parte centrale della distribuzione e le sue code. Questa relazione definisce alla "gobba" della distribuzione.
È opportuno sottolineare, infine, che l'istogramma si può modificare anche rispetto a due o a tutti e tre gli aspetti presi in considerazione: tendenza centrale, variabilità e forma.