Unit 4: indici di posizione (parte 3 di 3)
| Sito: | Federica Web Learning - LMS |
| Corso: | Statistica Psicometrica |
| Unit: | Unit 4: indici di posizione (parte 3 di 3) |
| Stampato da: | Utente ospite |
| Data: | sabato, 28 febbraio 2026, 06:07 |
Descrizione
- Tendenza centrale: indici analitici
- La centralità
- La centralità: le medie trimmed
- Notazione (digressione)
- La media aritmetica
- Proprietà della media aritmetica
- Media aritmetica per dati raggruppati in classi
Indice Unit
- 1. Tendenza centrale: indici analitici
- 2. La centralità
- 3. La centralità: le medie trimmed
- 4. Notazione
- 5. Notazione base
- 6. La media aritmetica
- 7. Proprietà della media aritmetica (1)
- 8. Proprietà della media aritmetica (2)
- 9. Proprietà della media aritmetica (3)
- 10. Proprietà della media aritmetica (4)
- 11. Proprietà della media aritmetica (5)
- 12. Media aritmetica per dati raggruppati in classi
1. Tendenza centrale: indici analitici
- Le misure di tendenza centrale basate sulle medie di posizione non richiedono calcoli analitici per la loro determinazione, è necessario individuare la modalità (o la classe) corrispondente e registrarne la modalità.
- Le misure di tendenza centrale basate su medie analitiche presuppongono, invece, una sintesi delle modalità osservate attraverso una opportuna funzione matematica.
- Poiché gli operatori aritmetici sono una prerogativa esclusiva delle variabili quantitative, queste ultime sono le uniche per i quali sono ammesse le medie analitiche.
- Le medie analitiche si distinguono in medie lasche e medie ferme.
- Le medie lasche prendono in considerazione solo alcune specifiche modalità.
- Le medie ferme considerano tutte le modalità osservate.
2. La centralità
Il valore centrale della serie, che generalmente indichiamo con il simbolo \(c\), rappresenta il concetto più semplice e soprattutto più intuitivo di media analitica. Il valore centrale della generica variabile \(X\) è definito attraverso la semisomma degli estremi della serie
\[c(X) = \frac{\max(X) + \min(X)}{2}.\]
Consideriamo la generica serie (banale) \[1; 2; 3; 4; 5,\] il valore centrale sarà \[c = \frac{5+1}{2} = 3 .\]
Se sostituiamo il valore \(5\) della serie con il valore \(9\), avremo che \[c =\frac{9+1}{2} =5.\]
Come si può osservare, a differenza della mediana che non modifica il suo valore in seguito a questa perturbazione della serie (rimanendo inalterata e uguale 3), il valore centrale passa da 3 a 5, dimostrando la sensibilità delle medie analitiche (in generale) rispetto alla presenza di valori anomali.
3. La centralità: le medie trimmed
Una possibile soluzione per limitare l'influenza dei valori estremi sul valore centrale \(c\) consiste nel considerare solo la parte più centrale della distribuzione trimmed. Si fissa un livello di taglio della serie, se ne determina il quantile corrispondente e si procede al calcolo della semisomma dei quantili desiderati. Le medie trimmed più diffusamente utilizzate sono definite attraverso la semisomma del terzo e del primo quartile $$ c_{(50)}(X) = \frac{Q_3(X) + Q_1(X)}{2} $$ e la semisomma del novantacinquesimo e quinto percentile $$ c_{(90)}(X) = \frac{P_{95}(X) + P_{5}(X)}{2}. $$ Osservare che l'indice \(c_{(50)}(X)\) tiene conto della metà più centrale della serie, mentre l'indice \(c_{(90)}(X)\) considera il \(90\%\) della serie.4. Notazione
Digressione: l'importanza della notazione
In qualsiasi tipo di comunicazione esistono regole ben precise e rigorose che vanno accuratamente rispettate per avere una comunicazione corretta.
La statistica si serve della notazione matematica per definire i suoi concetti. Ciò vuol dire che la notazione è molto importante. Un uso improprio della notazione in matematica (e quindi anche in statistica) equivale a commettere grossolani errori di ortografia quando si scrive.
Errori di questo tipo:
«Vado ha casa» oppure «Il sonno da sollievo.»
rappresentano piccolissime varianti grafiche delle forme ortograficamente corrette, ma rappresentano errori grossolani e gravissimi che non danno alla frase il suo senso compiuto, sebbene è possibile immaginare che un ipotetico interlocutore possa comunque comprendere il senso del messaggio. Il fatto che il messaggio sia comprensibile non ne giustifica l'errore in ogni caso. Stessa cosa vale per la matematica. L'uso di una notazione approssimativa verrà notato come facendo perdere valore anche a contenuti che sono potenzialmente corretti.
5. Notazione base
\(X\) Le lettere latine in maiuscolo corsivo sono utilizzate per riferirsi ad una generica variabile.\(x_{i}\) La notazione \(x_{i}\) indica un generico valore assunto dalla variabile \(X\) in corrispondenza della unità statistica individuata dal pedice \(i\) e lo leggiamo "\(x\) con \(i\)".
Se utilizziamo un pedice è necessario indicare quali valori può assumere. Quindi, se definiamo \(X: x_i\) dobbiamo anche specificare quali valori può assumere \(i\), scriveremo, quindi: \(X: x_i\) dove \(i=1,\ldots, N\), che chiameremo serie indicizzata e leggeremo come: "Data la variabile \(X\), tale che assume i valori \(x_1, x_2, \cdots, x_i, \cdots\) per \(i\) che va da \(1\) a \(N\)."
Più avanti utilizzeremo anche le lettere dell'alfabeto greco come \(\mu\), \(\sigma\), ecc.. Le lettere greche sono utilizzate per definire una caratteristica della popolazione. Per esempio, per convenzione la lettera \(\mu\) si riferisce alla media di una popolazione.
Useremo dei simboli anche per le funzioni matematiche. Il simbolo \(\sum\), per esempio, si chiama sommatoria e applicato ad una serie indicizzata sta ad indicare la somma di tutti i termini \[\sum_{i=1}^{N}{x_i}\] che si legge come "la somma dei valori di \(X\) per \(i\) che va da \(1\) a \(N\)".
6. La media aritmetica
Fra tutte le misure di tendenza centrale, analitiche e di posizione, la media aritmetica, per le proprietà di cui gode, occupa una posizione di rilievo.
Definizione della media aritmetica
Si definisce media aritmetica, che indicheremo con \(\bar{x}\),
la quantità determinata attraverso la somma di tutte le modalità osservate divisa per la numerosità del collettivo
$$\boxed{\bar{x} = \frac{\sum_{i=1}^{N}x_i}{N} = \frac{1}{N}\sum_{i=1}^{N}x_i}$$
La formula si legge in questo modo: "\(x\) sovrasegnato (oppure \(x\) bar) è uguale alla sommatoria delle \(x\) per \(i\) che va da \(1\) a \(N\)".
La media aritmetica deve la sua definizione al fatto che essa è il valore centrale della progressione aritmetica \(1; 2; \cdots; N\). Infatti la media aritmetica di \(1; 2\) è \(1,5\) che ne è anche il valore centrale, la media di \(1; 2; 3\) è uguale a \( (1+2+3)/3 = 6/3 =2\) e \(2\) è anche il valore centrale. Si potrebbe andare avanti... fino a \(\infty\).
7. Proprietà della media aritmetica (1)
Oltre alla internalità (criterio di Cauchy), che ne costituisce un requisito ancor prima di che una proprietà, la media aritmetica gode di 5 proprietà:La media aritmetica \(\bar{x}\) rappresenta la condizione di equidistribuzione del carattere, cioè se l'intero ammontare del carattere fosse divisibile in parti uguali all'interno del collettivo, ciascuna unità statistica avrebbe come modalità proprio la media aritmetica (criterio di Chisini) $$N\bar{x} = \sum_{i=1}^{N}{x_i}.$$ Per dimostrare questa proprietà è sufficiente dividere i termini dell'espressione precedente per \(N\) per ritornare alla definizione stessa di media aritmetica. In virtù di tale proprietà si dice che la media aritmetica vale solo per caratteri trasferibili e pertanto non può essere applicata a caratteri ordinali sebbene codificati su scala numerica.
Un carattere è trasferibile se ripartibile anche in quote non intere, almeno in senso astratto. In altre parole, sono ripartibili solo i caratteri quantitativi anche se misurati su scala discreta.
8. Proprietà della media aritmetica (2)
La somma degli scarti degli elementi di una serie \(X: x_1, x_2, \cdots, x_i, \cdots x_N\) da una generica media \(\min{(X)} \leq {\cal M} \leq \max{(X)}\) è \(0\) solo se \({\cal M}\equiv \bar{x}\) (criterio di Kolmogorov-De Finetti). Formalmente: \[\sum_{i=1}^{N}(x_i - \bar{x}) = 0.\] Dimostriamo:\[\sum_{i=1}^{N}(x_i - \bar{x}) = \sum_{i=1}^{N}{x_i} - \sum_{i=1}^{N}{\bar{x}} = \sum_{i=1}^{N}{x_i} - N\bar{x} = 0\]Portando a destra il secondo termine, dalla precedente proprietà:
\[\sum_{i=1}^{N}{x_i} = N\bar{x}_\blacksquare . \]
Osservare che la sommatoria si può portare all'interno della parentesi, si può distribuire, per la proprietà distributiva della somma aritmetica. Non sempre è possibile distribuire la sommatoria.
9. Proprietà della media aritmetica (3)
La media aritmetica è il centro di ordine 2 (criterio di Wald). Sia \({\cal M}\) una generica media (soddisfa il criterio della internalità), si dimostra che la funzione \[ \sum_{i=1}^{N}{(x_i - {\cal M})^2} = \min! \] vale se e solo se \({\cal M}\equiv \bar{x}\) è la media aritmetica.Dimostriamo
Per dimostrare bisogna: derivare la funzione rispetto alla variable \({\cal M}\)
\[ f'({\cal M}) = -2\sum_{i=1}^{N}{(x_i - {\cal M})},\]
porre la derivata a \(0\) e calcolare il valore di \({\cal M}\) che annulla l'equazione
\[
\begin{array}{rl}
2\sum_{i=1}^{N}{\cal M} - 2\sum_{i=1}^{N}{x_i} &= 0\cr N{\cal M} &= \sum_{i=1}^{N}{x_i}\cr {\cal M} &= \frac{1}{N}\sum_{i=1}^{N}{x_i}_\blacksquare
\end{array}
\]
Diremo, quindi, che la media aritmetica minimizza la funzione di perdita \( \sum_{i=1}^{N}{(x_i - {\cal M})^2}\).
10. Proprietà della media aritmetica (4)
Proprietà associativaSia \(X:x_1, x_2, \cdots, x_N\) una generica serie di \(N\) elementi con media \[ \bar{x} = \frac{1}{N}\sum_{i=1}^{N}{x_i}, \] scomponendo la serie in \(k\geq 2\) sottoinsiemi anche di numerosità non omogenea \(n_1, n_2, \cdots, n_k\), si dimostra che la media generale \(\bar{x}\) si può esprimere come media *ponderata* delle medie parziali \[ \bar{x} = \frac{\sum_{j=1}^{k}n_j\bar{x}_j}{\sum_{j=1}^{k}{n_j}}. \] La dimostrazione è molto semplice e la facciamo per \(k=2\) sapendo che per la proprietà (2): \[ \sum_{i=1}^{n_j}x_i = n_j\bar{x}_j \] e che \[ \sum_{j=1}^{k}n_j = N. \]
11. Proprietà della media aritmetica (5)
La media aritmetica è invariante per trasformazioni lineari di \(X\).Sia \(X:x_1, x_2, \cdots, x_N\) una generica serie di \(N\) elementi con media \[ \bar{x} = \frac{1}{N}\sum_{i=1}^{N}{x_i} \] Sia \(Y = X + a\), dove \(a\) è una costante, si dimostra che \[\bar{y} = \bar{x} + a. \] Analogamente consideriamo la serie \(W = bX\), dove \(b\) è una costante, si dimostra che \[ \bar{w} = b\bar{x}. \] Infine, se \(Z = a + bX\), allora \(\bar{z} = a + b\bar{x}\): \[ \bar{z} = \frac{1}{N}\sum_{i=1}^{N}{(a+bx_i)} = \frac{Na}{N} + \frac{Nb{\sum_{i=1}^{N}x_i}}{N} = a + b\bar{x}_{\blacksquare} \]
Attenzione: Invariante vuol dire che le trasformazioni su \(X: x_1, x_2, \cdots, x_i, \cdots, x_N\) si riflettono allo stesso modo anche su \(\bar{x}\).
12. Media aritmetica per dati raggruppati in classi
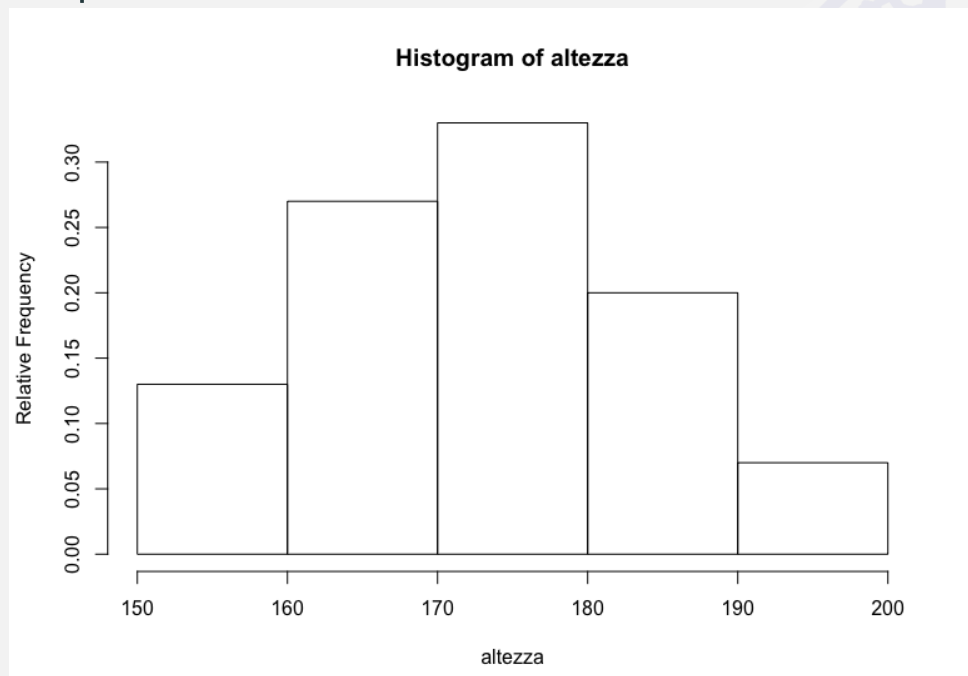
Calcolo della media aritmetica per dati raggruppati in classi. Consideriamo gli stessi dati degli esempi precedenti e il medesimo istogramma che ne descrive la distribuzione.
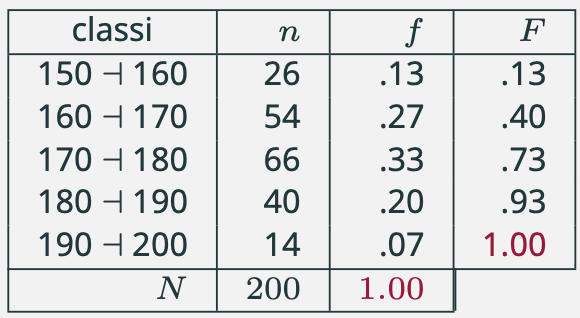
Istogramma e distribuzione delle frequenze assolute e relative per i dati relativi alla variabile altezza.
 |
 |
|---|
\([1;2;3]\) la media è 2,0
\(\vdots\)
\([1, \cdots, N]\) la media è \(\frac{1 + N}{2}\)
Se ne deduce, quindi, che la media corrisponde con il valore centrale o centralità se la successione è uniforme. Pertanto, in assenza di altre informazioni, assumiamo che la distribuzione delle osservazioni all'interno di ciascuna classe è una distribuzione uniforme e di conseguenza la media della classe corrisponde al valore centrale.
Se indichiamo con la lettera \(K\) il numero generico di classi e con la lettera \(k\) la generica classe, per cui possiamo scrivere che \(k=1,\ldots K\) (che \(k\) varia fra \(1\) e \(K\)), per la proprietà associativa della media aritmetica, possiamo determinare la media generale \(\bar{x}\) attraverso la media ponderata delle medie parziali di ciascuna classe. Avremo quindi
\[
\boxed{\bar{x} = \frac{\sum_{k=1}^{K}n_k \times c_k }{\sum_{k=1}^{K}n_k}}.
\]
Nell'esempio abbiamo che
\[
\bar{x} = \frac{155\times 26 + 165\times 54 + 175 \times 66 + 185 \times 40 + 195 \times 14 }{26+54+66+40+14} = 173,1.
\]
Naturalmente è possibile utilizzare le frequenze relative al posto delle frequenze assolute. In questo caso l'operazione sarà la seguente e il risultato lo stesso
\[
\bar{x} = 155\times 0,13 + 165\times 0,27 + 175 \times 0,33 + 185 \times 0,20 + 195 \times 0,07 = 173,1.
\]