Unit 3: curva normale ed uso delle tavole
| Sito: | Federica Web Learning - LMS |
| Corso: | Statistica Psicometrica |
| Unit: | Unit 3: curva normale ed uso delle tavole |
| Stampato da: | Utente ospite |
| Data: | lunedì, 23 febbraio 2026, 14:20 |
Descrizione
- La Curva Normale
- Dalla raccolta dei dati alle distribuzioni naturali
- Esempi di regolarità
- Una forma che si ripete
- La tavola della curva normale
- Uso della tavola
Indice Unit
- 1. La curva Normale /1
- 2. La curva Normale /2
- 3. La curva Normale /3
- 4. La curva Normale /4
- 5. La curva Normale /5
- 6. La curva Normale /6
- 7. La curva Normale /7
- 8. Dalla raccolta dei dati alle distribuzioni naturali
- 9. Esempi di regolarità /1
- 10. Esempi di regolarità /2
- 11. Esempi di regolarità /3
- 12. Esempi di regolarità /4
- 13. Una forma che si ripete /1
- 14. Una forma che si ripete /2
- 15. Una forma che si ripete /3
- 16. Una forma che si ripete /4
- 17. Una forma che si ripete /5
- 18. Una forma che si ripete /6
- 19. Uso della tavola della Normale /1
- 20. Uso della tavola della Normale /2
1. La curva Normale /1
Il contributo di Gauss e Laplace
Johann Friedrich Carl Gauss (1777-1855) e Pierre-Simon Laplace (1749-1827) sono fra le più importanti ed influenti figure della matematica del IXX secolo.
Gauss era tedesco e Laplace francese. Nonostante all’inizio del secolo i rapporti fra le due potenze erano tesi a causa della ascesa di Napoleone, sappiamo che Gauss e Laplace si sono incontrati almeno una volta a Parigi in occasione del primo congresso scientifico della storia dell’umanità, fra il 1798-1799, organizzato per presentare al mondo intero la rivoluzionaria idea del sistema metrico-decimale.
Tutti i matematici invitati al congresso erano impegnati a lavorare sui dati prodotti dai geodeti Mechant e Dalambre relativi alla misura del quarto di meridiano terrestre, la cui decimilionesima parte sarebbe diventanto il metro.
Ogni misura veniva ripetuta più e più volte e gli scienziati erano consapevoli in maniera euristica che ogni misurazione sarebbe stata affetta da un errore (l’errore di misura) e che la media aritmetica delle misure è la migliore rappresentazione della vera misura.
2. La curva Normale /2
Gauss e Laplace, in maniera indipendente ma senza ignorare il lavoro dell’altro (e sulla base dei risultati già noti di De Moivre), erano alla ricerca di un modello matematico - di semplice manipolazione - in grado di descrivere il comportamento degli errori di misura.
La prima curva degli errori di Laplace aveva questa funzione
\[ \phi(x) = \dfrac{m}{2} e^{m|x|} \, , \]
dove \(m = 1\) è un parametro di variabilità dell’errore.

3. La curva Normale /3
Gauss e Laplace, in maniera indipendente ma senza ignorare il lavoro dell’altro (e sulla base dei risultati già noti di De Moivre), erano alla ricerca di un modello matematico - di semplice manipolazione - in grado di descrivere il comportamento degli errori di misura.
La seconda funzione degli errori di Laplace aveva questa espressione:
\[ \phi(x) = \frac{1}{2a} \ln\left( \dfrac{a}{|x|} \right) \, , \]
dove \(a > 0\) è un parametro di variabilità dell’errore.

4. La curva Normale /4
Laplace era giunto a questi modelli perché - e lo sappiamo dai suoi scritti - conosceva il valore di centralità della successione aritmetica \( \displaystyle \dfrac{1}{n}\sum_{i=1}^n x_i\) per \(n\longrightarrow \infty\):
Distribuzione delle frequenze dei punteggi medi lancio di 1 dado
Distribuzione delle frequenze dei punteggi medi lancio di 2 dadi
Distribuzione delle frequenze dei punteggi medi lancio di 3 dadi
Distribuzione delle frequenze dei punteggi medi lancio di 4 dadi
Distribuzione delle frequenze dei punteggi medi lancio di 5 dadi
5. La curva Normale /5
Distribuzione delle frequenze dei punteggi medi lancio di 6 dadi
Distribuzione delle frequenze dei punteggi medi lancio di 7 dadi
Distribuzione delle frequenze dei punteggi medi lancio di 8 dadi
Distribuzione delle frequenze dei punteggi medi lancio di 9 dadi
Distribuzione delle frequenze dei punteggi medi lancio di 10 dadi
6. La curva Normale /6
- Ciò che Laplace aveva osservato studiando la distribuzione della media aritmetica dei punteggi relativi al lancio di un dado ripetuto \(n = 1, 2, \dots , \infty\) volte era la tendenza della distribuzione ad assumere una forma campanulare.
- In altre parole, considerando \(n = 2\) (due lanci), le combinazioni possibili e le relative medie sono: \((1 + 1)/2 = 1, (1 + 2)/2 = 1, 5, (1 + 3)/2 = 2, · · · , (6 + 6)/2 = 6\).
Si osserva che, mentre le medie 1 e 6 si verificano solo con la combinazione \(\{1; 1\}\) e \(\{6; 6\}\), rispettivamente, la media \(3\), \(5\) si verifica con le sei combinazioni \(\{1; 6\}\), \(\{2; 5\}\), \(\{3; 4\}\), \(\{4; 3\}\), \(\{5; 2\}\) e \(\{6; 1\}\).
- Se \(n\) aumenta, le combinazioni che hanno come media \(1\) e \(6\) saranno sempre una per ciascun valore, mentre aumenta (in ragione esponenziale) il numero di combinazioni che producono valori intermedi. Più di tutte aumenta il numero di combinazioni che ha come media \(3\), \(5\).
- La distribuzione delle medie tende ad assumere la forma Normale.
7. La curva Normale /7
Fu Gauss, però, a comprendere la necessità di passare a considerare gli scarti dalla media al quadrato. La denominazione di Curva Normale o distribuzione Normale la dobbiamo a K. Pearson molto tempo dopo.
La curva Normale o curva di Gauss (Normal distribution)
\[ f(x) = \dfrac{1}{\sqrt{2\pi\color{brown}{\sigma}^2}}{\sf e}^{-\frac{1}{2}\left( \frac{x-\color{brown}{\mu}}{\color{brown}{\sigma}}\right)^2} \]
dove:
- \( \pi = 3,14159265358979\dots \)
è un numero irrazionale (che corrisponde al rapporto fra la lunghezza di una circonferenza e il suo diametro);
- \( {\sf e} = 2,7182818284590\dots \)
è un numero irrazionale che corrisponde al limite per \(n \rightarrow \infty\) delle due successioni:\[ {\sf e} = \lim_{n\to\infty} \left( 1 + \dfrac{1}{n} \right)^n \]
\[ {\sf e} = \sum_{n=0}^{\infty} \dfrac{1}{n!} \]
- \(\color{brown}{\mu}\) e \(\color{brown}{\sigma}\) sono parametri. \(\color{brown}{\mu}\) è la media aritmetica (e coincide con mediana e moda), e \(\color{brown}{\sigma}\) è la deviazione standard (scarto quadratico medio) della distribuzione.
8. Dalla raccolta dei dati alle distribuzioni naturali
In the eighteenth century, governments began collecting, tabulating and organizing data about the people as a means to eective governance. These data management activities have grown ever more complex with time. Mendel’s nineteenth century theory of genetics brought probability and statistics into the heart of science.
K. Blackmond Laskey and L. Martignon, 2010L’osservazione sistematica dei dati raccolti evidenziò che alcune tipologie di distribuzioni presentavano regolarità che si ripetevano sistematicamente.
L’evidenza empirica stava dimostrando che esistono famiglie di caratteri che, indipendentemente dalla popolazione su cui sono stati osservati, assumono distribuzioni che hanno sempre la stessa forma.
9. Esempi di regolarità /1
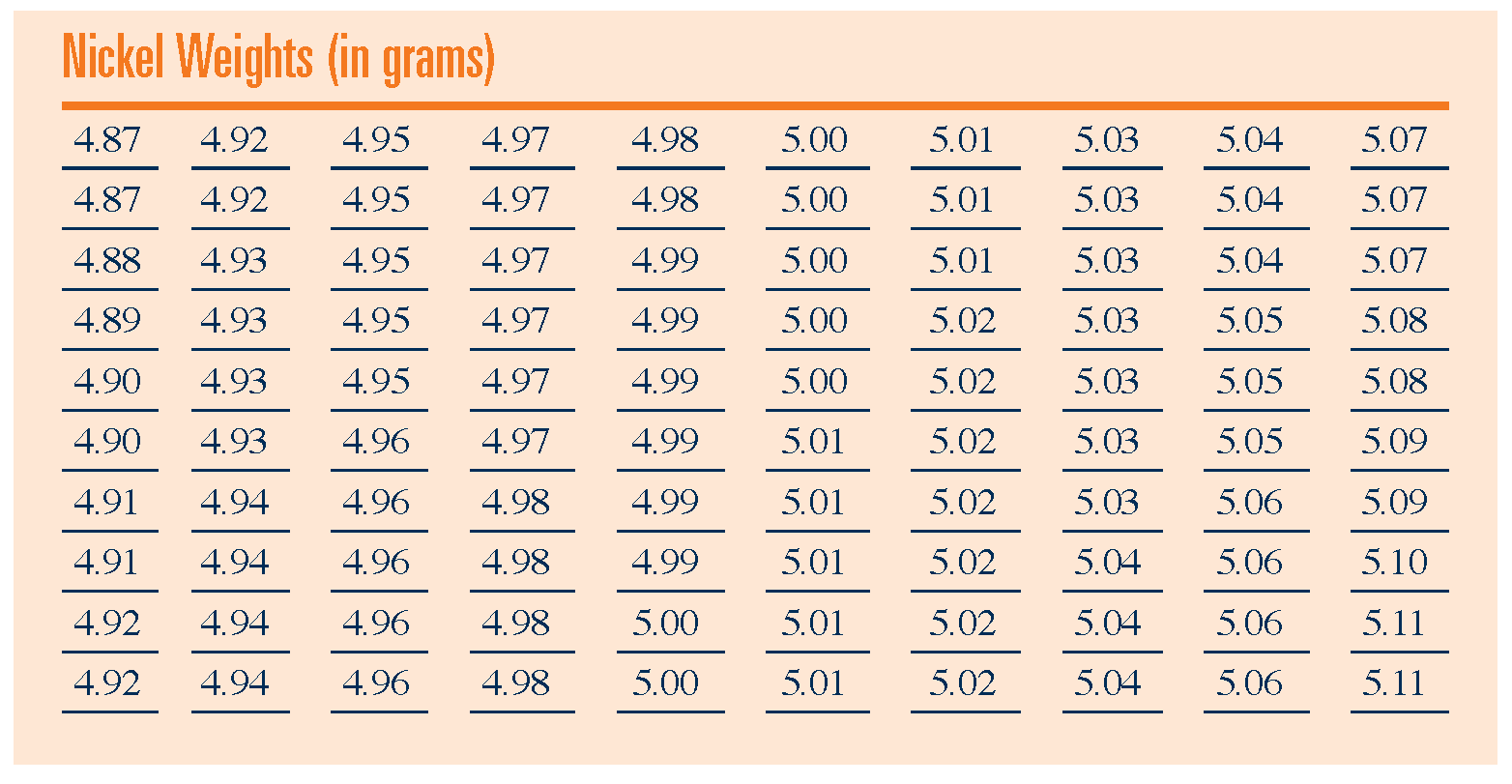
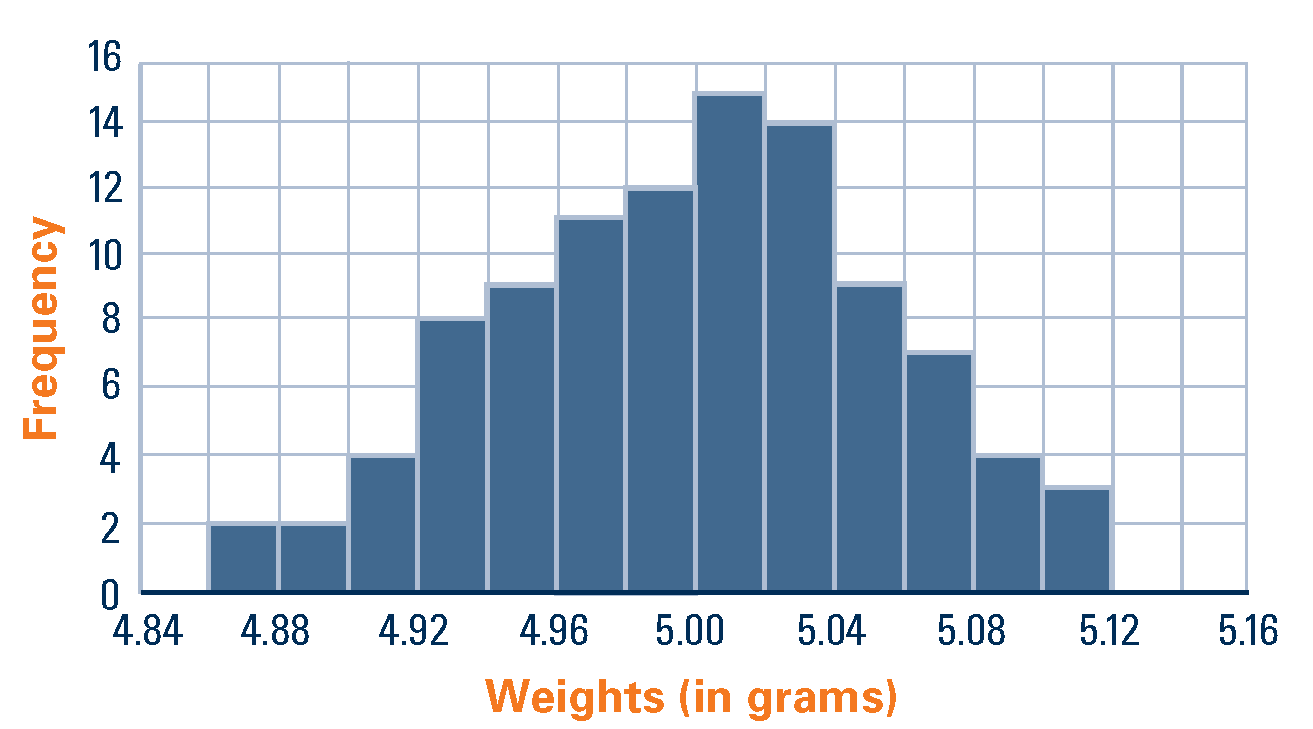
10. Esempi di regolarità /2
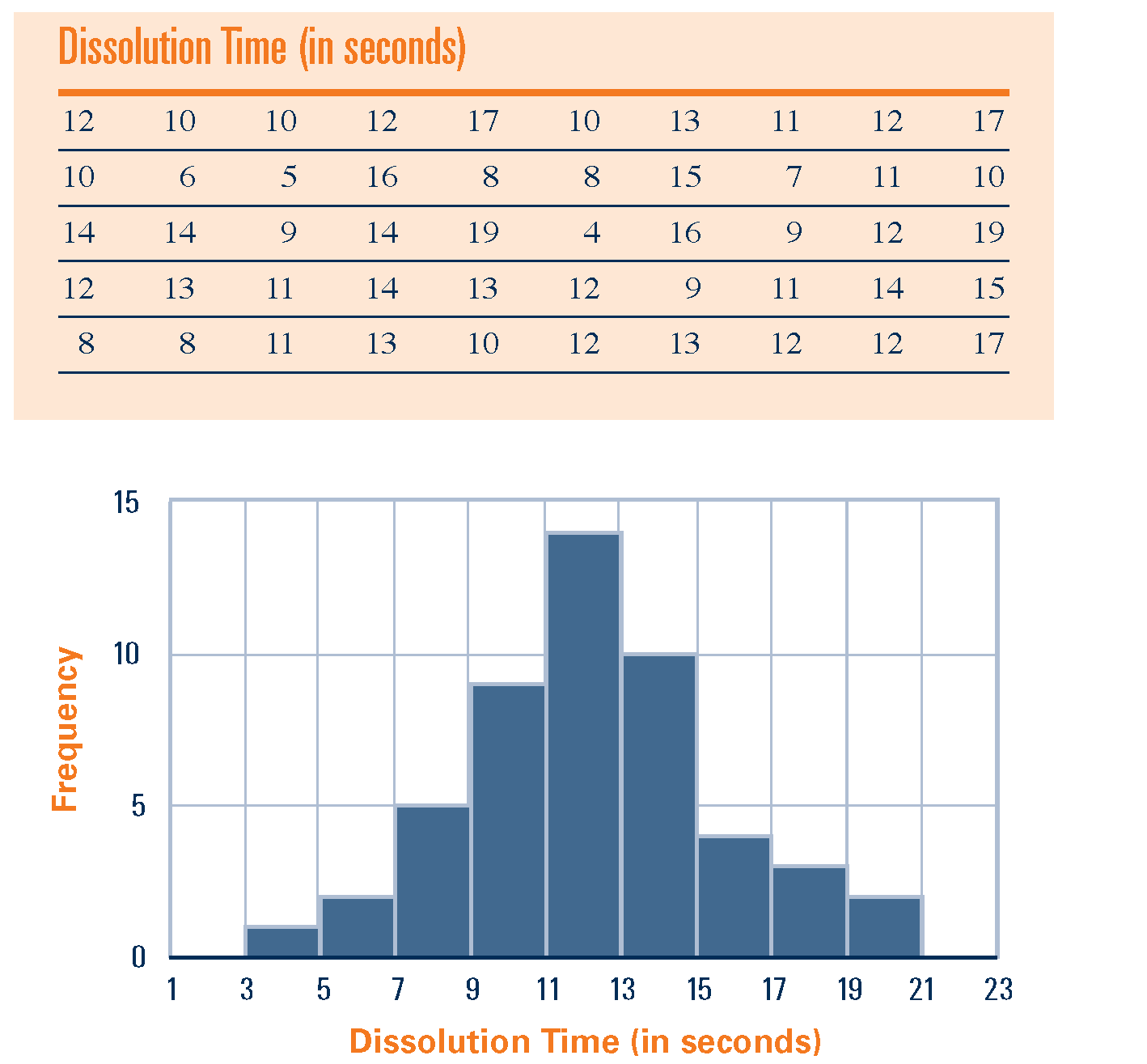
11. Esempi di regolarità /3
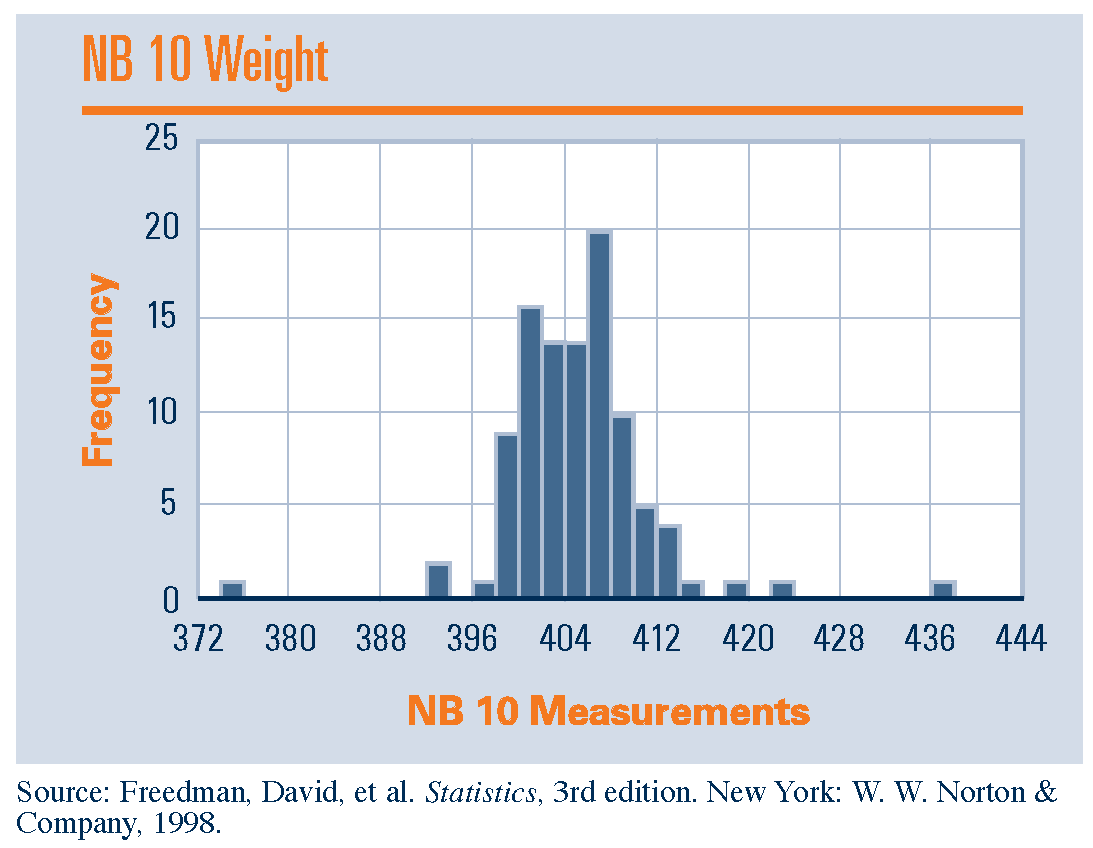
12. Esempi di regolarità /4
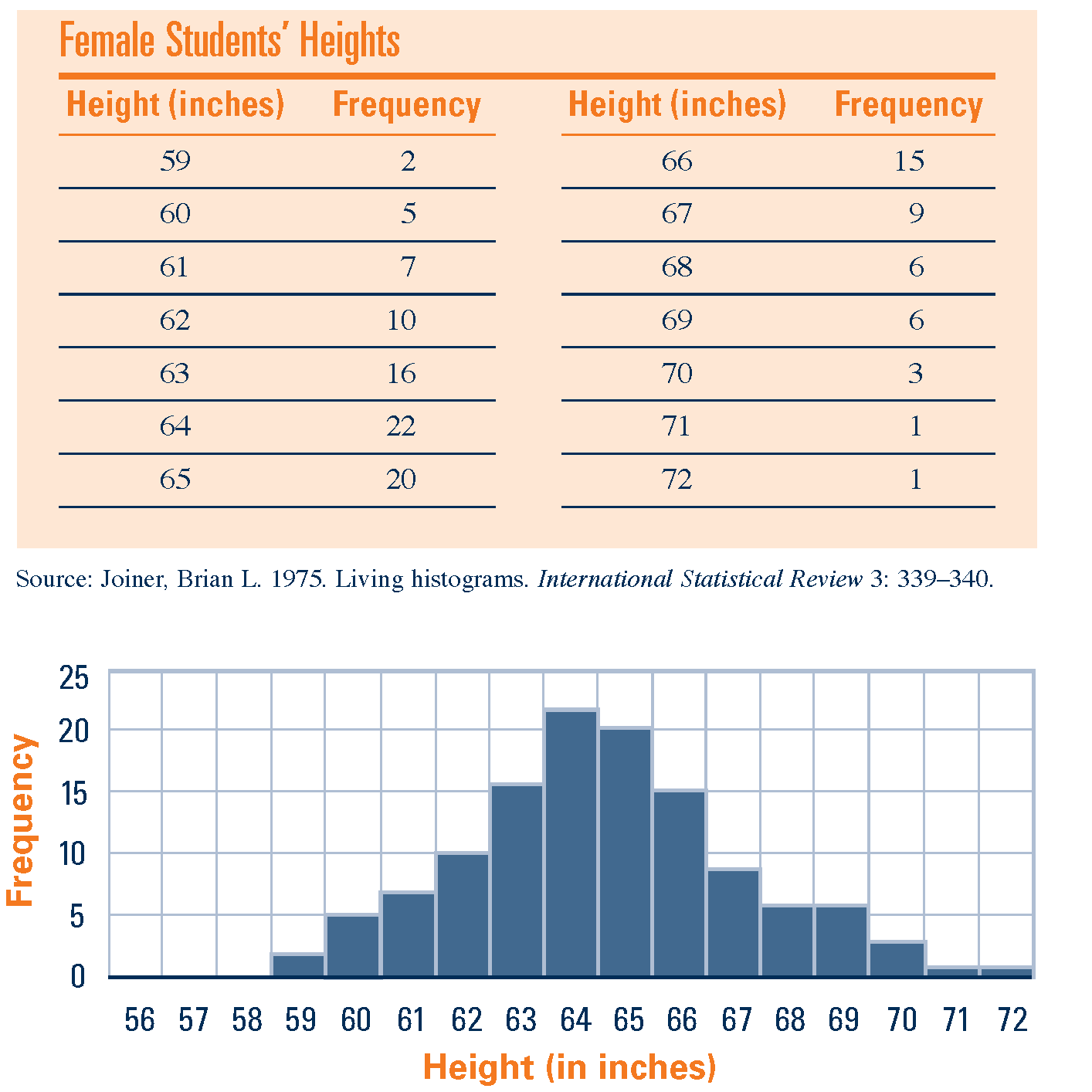
13. Una forma che si ripete /1
Cosa hanno in comune tutte queste distribuzioni?- Se le distribuzioni possono essere descritte attraverso i loro momenti, queste distribuzioni quali momenti hanno in comune?
\(M^1\) Tendenza centrale → No
\(M^2\) Variabilità → No\(M^3\) Asimmetria → Sì
\(M^4\) Curtosi → Sì
- essere definita sull’intero supporto della variabile (cioè su \(\mathbb{R}\));
- avere un parametro per la tendenza centrale;
- avere un parametro per la variabilità;
- essere simmetrica;
- avere un rapporto costante e uguale a 3 fra il momento centrato di ordine 4 e il quadrato del momento secondo centrato: \( \dfrac{m^4_{(\bar{x})}}{(\sigma^2)^2} = 3\) (normocurtosi).
14. Una forma che si ripete /2
La curva Normale o curva di Gauss si presenta così
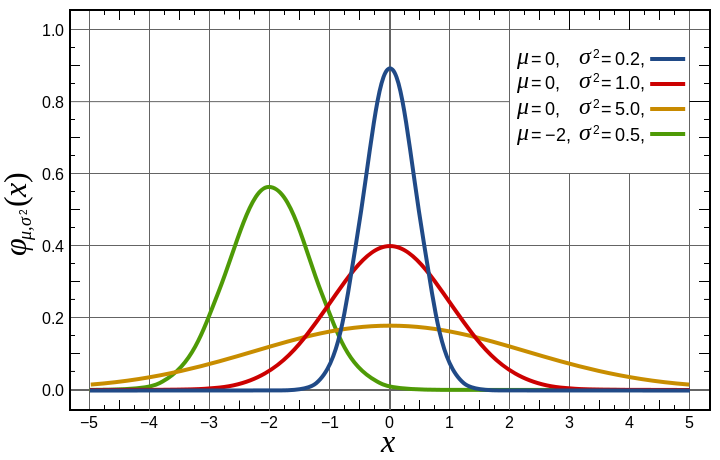
Funzione di densità di frequenza
15. Una forma che si ripete /3
La curva Normale o curva di Gauss si presenta così
Funzione di ripartizione
16. Una forma che si ripete /4
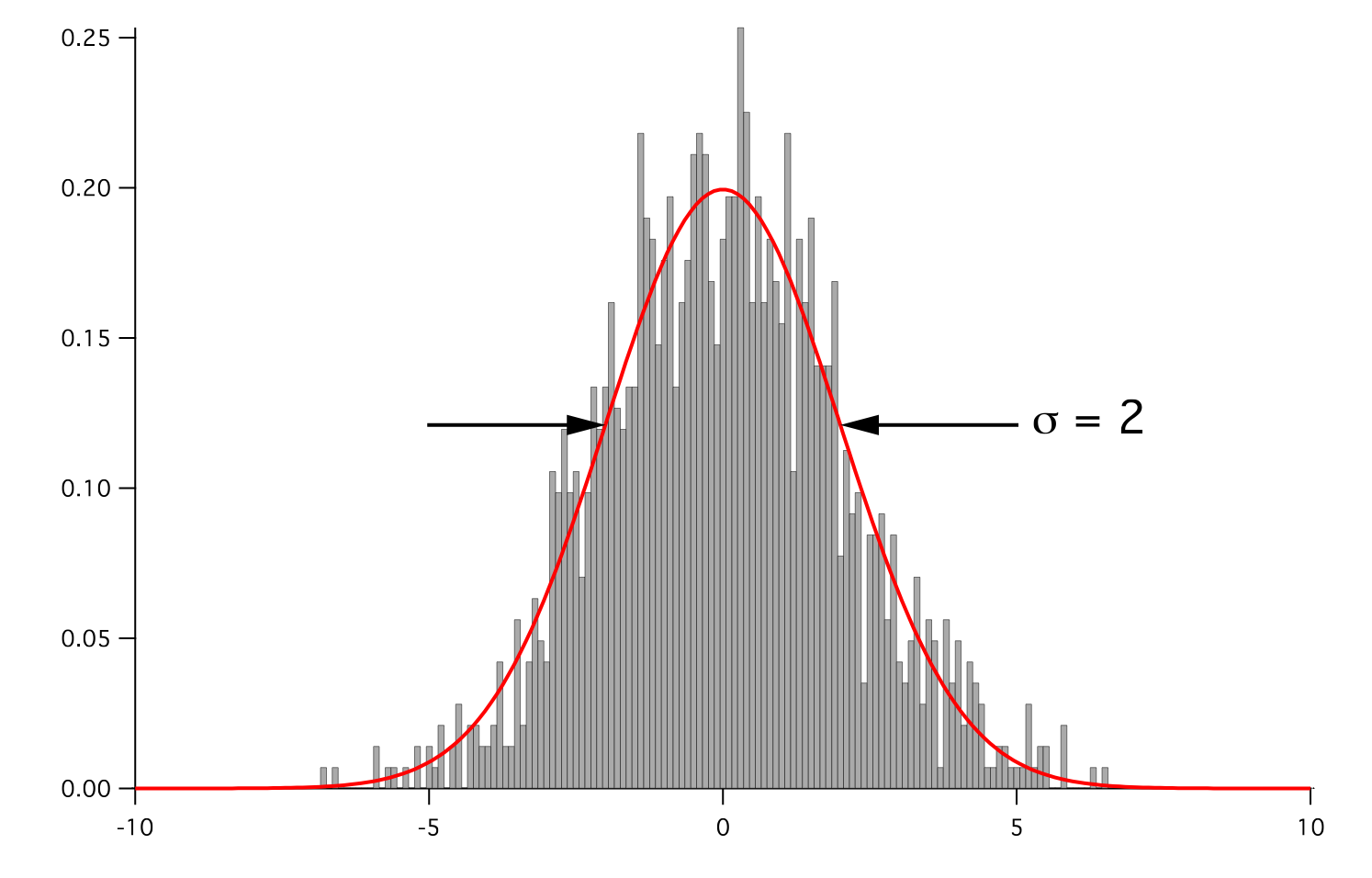
La curva Normale o curva di Gauss
Una funzione teorica non è altro che un istogramma dove l’ampiezza delle classi \(a \rightarrow 0\) per \(N \rightarrow \infty\).
17. Una forma che si ripete /5
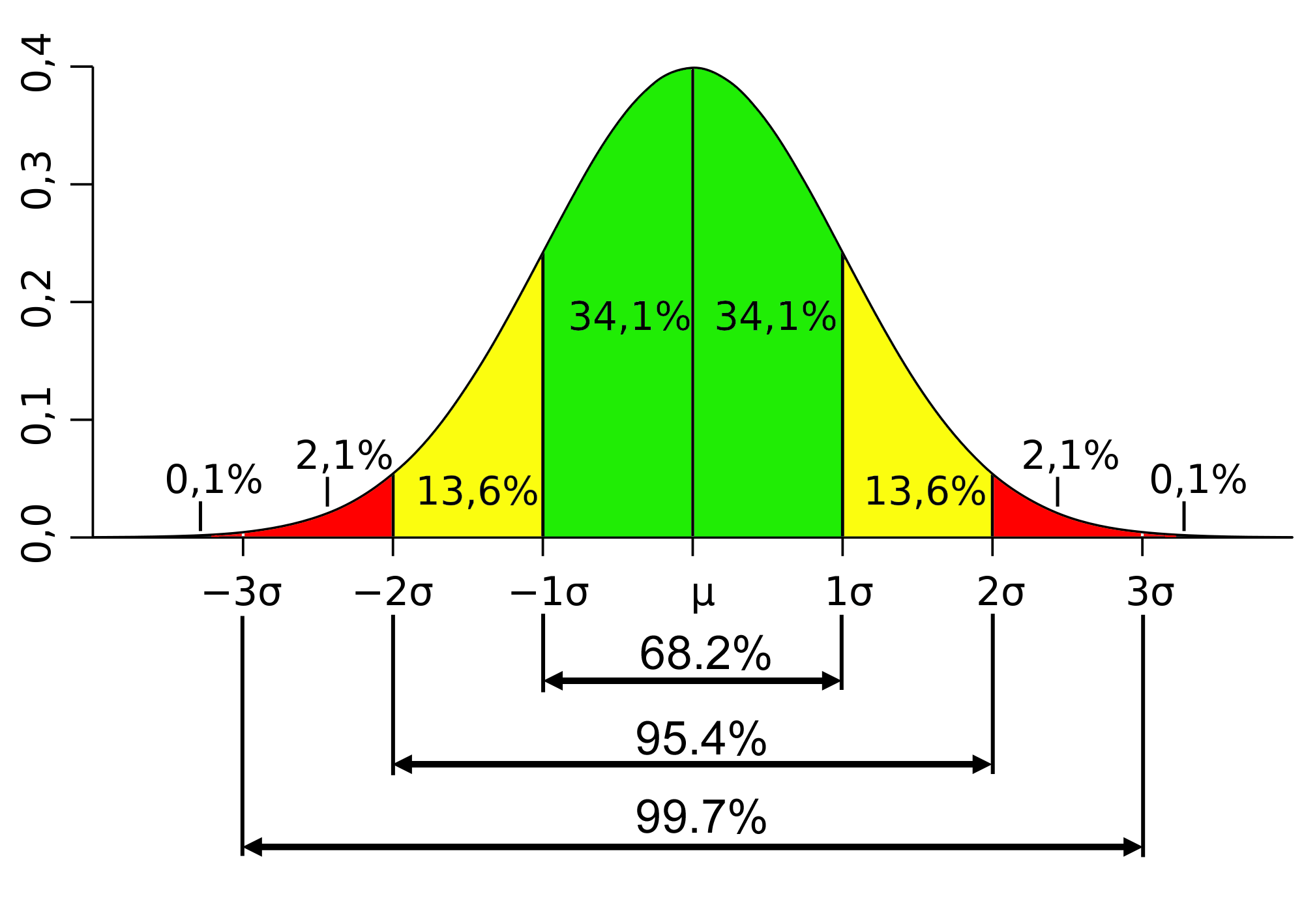
Proprietà della Curva Normale- È definita su tutto l’asse \(\mathbb{R}\);
- È asintotica rispetto all’asse \(X\);
- È simmetrica;
- È normocurtica e rispetta le proporzioni, in termini area, illustrate in figura.
18. Una forma che si ripete /6
La Curva Normale standard
Se effettuiamo un cambiamento di variabile, da \(X\) a \(Z\), avremo:
\[ \begin{array}{l} Y = X - \bar{x} \\[3pt] Z = \dfrac{Y}{\sigma_X} \\[3pt] Z = \left( \dfrac{X-\bar{x}}{\sigma_X} \right) \longrightarrow \bar{Z} = 0 \text{ e } \sigma_Z^2 = 1 \\[3pt] f(Z) = \dfrac{1}{\sqrt{2\pi\color{red}{1^2}}}{\sf e}^{-\frac{1}{2}\left( \frac{z-\color{red}{0}}{\color{red}{1}} \right)^2} \\[3pt] f(Z) = \dfrac{1}{\sqrt{2\pi}}{\sf e}^{-\frac{1}{2} \frac{z^2}{2}} \end{array} \]
19. Uso della tavola della Normale /1
Sia \(X\) una variabile statistica tale che \( X \sim N(\mu, \sigma^2) \) e assumiamo che essa rappresenti la distribuzione teorica della spesa mensile dei clienti di una compagnia elettrica, dove \(\mu = 23,5\) e \(\sigma^2 = 27,04 \; (\sigma = 5,2)\).
La compagnia vuole proporre uno sconto al \(10\%\) dei clienti che hanno speso di più.
Soluzione:
Utilizzando la tavola della curva normale bisogna individuare il novantesimo percentile sulla curva standardizzata: \(F(Z) = 0,9\), vediamo che \(z = 1\), \(28\). Quindi \(1,28\) è il \(90\)esimo percentile della curva che ha media \(0\) e varianza \(1\). Utilizzando la funzione inversa della standardizzazione, trasformiamo \(Z\) in \(X\).
\[ x = z ∗ \sigma + \mu = 1,28 ∗ 5,2 + 23,5 = 30,16 \]
20. Uso della tavola della Normale /2
Sia \(X\) una variabile statistica tale che \(X \sim N(\mu, \sigma^2)\) e assumiamo che essa rappresenti la distribuzione teorica della spesa mensile dei \(328000\) clienti di una compagnia elettrica, con \(\mu = 23,5\) e \(\sigma^2 = 27,04\).
La compagnia vuole sapere quanti sono i clienti che hanno speso più di \(15\) Euro e meno di \(25\) Euro (la media è compresa nell’intervallo).
Soluzione:
Osserviamo che l’intervallo comprende la media \(\mu = 23,5\), il calcolo dell’area va sviluppato in due parti: prima e dopo la media.
\[ z = (15 − 23,5)/5,2 = −1,63 , \]
\(F(−1,63) = 1 − F(1,63) \). A noi interessa la frequenza compresa fra \(0\) e \(1,63\), che corrisponde a \(0,44845\) e la frequenza compresa fra \(0\) e \(z = (25 − 23,5)/5,2 = 0, 29 \) che vale \(0,114\). La frequenza relativa è \(f = 0, 44845 + 0, 11400 = 0, 56254\). La frequenza assoluta corrispondente è \(n = 0, 56254 ∗ 328000 = 184514\).