Unit 1 - Cenni di Calcolo delle Probabilità
| Sito: | Federica Web Learning - LMS |
| Corso: | Statistica Psicometrica |
| Unit: | Unit 1 - Cenni di Calcolo delle Probabilità |
| Stampato da: | Utente ospite |
| Data: | lunedì, 19 gennaio 2026, 01:22 |
Indice Unit
- 1. Il ritardo del 34!
- 2. ... e altre storie interessanti.
- 3. La scoperta della probabilità e la nascita del calcolo delle probabilità /1
- 4. La scoperta della probabilità e la nascita del calcolo delle probabilità /2
- 5. Dagli Egiziani fino al 1525 /1
- 6. Dagli Egiziani fino al 1525 /2
- 7. La possibilità
- 8. Riferimenti storici fondamentali
- 9. Dal problema del Cavalier De Meré a Daniel Kahneman
- 10. Innumeracy
- 11. Cosa vuol dire Innumeracy?
- 12. Il problema del Cavalier de Meré /1
- 13. Il problema del Cavalier de Meré /2
- 14. Concetti primitivi
- 15. Assiomi della probabilità
- 16. Spazio campionario
- 17. Esiti ed eventi
- 18. Unione e intersezione di eventi
- 19. Notazioni
- 20. Esempi
- 21. Probabilità
- 22. Soggettivisti e Frequentisti /1
- 23. Soggettivisti e Frequentisti /2
- 24. Eventi Indipendenti
- 25. Il problema del Cavalier de Meré - I due giochi dei dadi /1
- 26. Il problema del Cavalier de Meré - I due giochi dei dadi /2
- 27. Il problema del Cavalier de Meré - I due giochi dei dadi /3
- 28. Il problema del Cavalier de Meré - I due giochi dei dadi /4
- 29. Il problema del Cavalier de Meré - I due giochi dei dadi /5
- 30. La teoria della probabilità
- 31. Probabilità condizionata /1
- 32. Probabilità condizionata /2
- 33. Probabilità condizionata /3
- 34. Probabilità condizionata /4
- 35. Probabilità condizionata /5
- 36. Teorema di Bayes /1
- 37. Teorema di Bayes /2
- 38. Teorema di Bayes /3
- 39. Teorema di Bayes /4
- 40. Teorema di Bayes /5
- 41. Teorema di Bayes /6
- 42. Il problema di Monty Hall /1
- 43. Il problema di Monty Hall /2
- 44. Il problema di Monty Hall /3
- 45. Il problema di Monty Hall /4
- 46. Il problema di Monty Hall /5
- 47. Il problema di Monty Hall /6
- 48. Il problema di Monty Hall /7
- 49. Il problema di Monty Hall /8
- 50. Il problema di Monty Hall /9
- 51. Il problema di Monty Hall /10
- 52. Variabili casuali (v.c.) /1
- 53. Funzioni di distribuzione di probabilità
- 54. Funzioni di densità di probabilità
- 55. Valore atteso e Varianza di una v.c. /1
- 56. Valore atteso e Varianza di una v.c. /2
- 57. Momenti v.c.
- 58. Funzioni di distribuzione di probabilità
- 59. Funzioni di ripartizione o delle probabilità cumulate
- 60. v.c. di Bernulli /1
- 61. v.c. di Bernulli /2
- 62. Valore atteso e varianza della v.c. di Bernulli /1
- 63. Valore atteso e varianza della v.c. di Bernulli /2
- 64. v.c. Binomiale /1
- 65. v.c. Binomiale /2
- 66. v.c. Binomiale /3
- 67. v.c. Binomiale /3
- 68. v.c. Binomiale /4
- 69. v.c. Binomiale /5
- 70. v.c. Binomiale /6
1. Il ritardo del 34!
Da![]() del 30 agosto 1985.
del 30 agosto 1985.
Diciamola tutta la verità, nient’altro che la verità: il “34” a Napoli non piace, non è mai piaciuto, forse - dopo cinque secoli di lotto - non ha più nessuna possibilità di piacere. Se la città del Vesuvio rovescia da settimane fior di miliardi (di lire) su un numero che già nella “smorfia” ha un significato ostinatamente ostile - “Capatosta”, testa dura - lo si deve al lungo “sonno” di 146 settimane che mette sul chi vive ogni “lottista” che si rispetti dalla Sicilia al Piemonte. E d’altronde il quesito - uscirà finalmente il 34 sulla ruota di Napoli? - appassiona Bologna come Genova, Torino come Milano.

E fu solo il 28 dicembre 1985, quando finalmente venne estratto dall’urna sulla ruota di Napoli, dopo l’astronomica cifra di ben 163 estrazioni di ritardo, tuttora ritardo storico, che il 34 interruppe la sua latitanza.
Su Capatosta vennero giocati molti miliardi di Lire al botteghino, e molti miliardi in più nelle attività di lotto clandestino.
Per esorcizzare il fato avverso, al tempo, vennero organizzati rosari in chiesa ed altri riti propiziatori e non mancarono “esoneri” di bimbi bendati “colpevoli“ di non aver tirato fuori dall’urna il 34 latitante.
2. ... e altre storie interessanti.
- Il ritardo del 34 sulla ruota Napoli è solo una delle tante storie in cui è evidente la fallacia umana di fronte al caso.
- È anche vero che è proprio la difficoltà e il fascino di misurarsi con il caso che è alla base di qualsiasi successo dell’uomo: inteso sia come singolo sia come genere umano.
- In realtà - come vedremo alla fine di questa storia - sarà molto difficile stabilire cos’è il caso e cos’è casuale.
- Senza una rigorosa formulazione matematica delle leggi del “caso”, il rischio di essere ingannati dall’alea investe anche chi per formazione conosce i princîpi generali che governano gli eventi casuali.
3. La scoperta della probabilità e la nascita del calcolo delle probabilità /1
- Il fascino prodotto dalla possibilità di ottenere un successo e l’incertezza che governa il processo per giungere al successo definiscono una combinazione in grado di suscitare meccanismi di azione (anche sconsiderati) per ottenere il successo.
- Il gioco d’azzardo è la manifestazione più effimera, ma forse anche la più affascinante, in cui successo è rappresentato nella sua forma più seducente: la vincita in danaro, e il meccanismo è regolato solo dalle leggi del caso.
- Il binomio azzardo-vincita ha inevitabilmente determinato che la storia del calcolo delle probabilità passasse per il gioco d’azzardo.
4. La scoperta della probabilità e la nascita del calcolo delle probabilità /2
I passi del gambero- Lo studio della storia del calcolo delle probabilità ha evidenziato come il concetto di probabilità sia stato formalizzato molti anni dopo che fosse giunti alla definizione dei princîpi fondamentali del Calcolo delle probabilità.
- Nei primi trattati sulle leggi del caso si parla di possibilità e non di probabilità.
- È da notare che la parola probabilità deriva dal verbo latino probo, probas, cioè provare.
5. Dagli Egiziani fino al 1525 /1
- Sebbene il gioco (soprattutto quello dei dei dadi o degli astragali) fosse conosciuto sin dai tempi degli antichi egizi, fino al al 1500 (circa) non si è avuta la consapevolezza che le leggi del caso che sovrintendono il gioco dei dadi governano anche la vita di tutti i giorni.

- Per gli antichi tutto ciò che avveniva “per caso” era il frutto dei capricci degli dei.
- Gli scavi dell’antica Pompei hanno riportato alla luce moltissimi dadi, di fattura e materiali diversi e anche truccati.

- Anche il gioco Capita aut navia era molto apprezzato e diffuso.

- Si giocava così tanto che si rese necessaria una severa regolamentazione con pene altrettanto severe per il gioco d’azzardo. Una originale lex de aleatoribus, menzionata anche Plauto, sanzionava i giocatori d’azzardo.
6. Dagli Egiziani fino al 1525 /2
- In ogni caso dal tempo degli antichi egizi fino al 1500 non si fecero molti progressi nello studio del calcolo delle probabilità.
- Il gioco e in particolare il gioco d’azzardo era considerato un vizio ed un peccato.
- Le forze Divine erano considerate le uniche in grado di governare le sorti dell’uomo e dell’umanità.
- In effetti anche la matematica stessa faticava a fare progressi e si viveva nella paura dell’accusa di eresia. Il tribunale della Santa inquisizione lavorava a pieno regime. Pene severe e la pena di morte venivano comminate con grande facilità.
7. La possibilità
Gerolamo Cardano- Sebbene il 24 agosto 1654 sia considerata universalmente la data ufficiale che segna la nascita della Teoria del Calcolo delle Probabilità, giorno in cui Pascal inviò a Fermat una famosa lettera, va ricordato che tra il 1613 e il 1623 Galileo Galilei pubblicò il trattato Sopra le scoperte de i dadi.
- Il contributo più importante fu però quello di Gerolamo Cardano (1501-1576). Il suo trattato sulla Teoria della Possibilità, il Liber de ludo aleae, fu pubblicato postumo, solo nel 1663. Si presume che Cardano lo abbia iniziato scrivere ancora giovanissimo fra il 1522 e il 1525.
- Bisognerebbe approfondire lo studio della persona di Cardano per comprendere come sia potuto accadere.


8. Riferimenti storici fondamentali
La nascita teoria della probabilità viene fatta coincidere con la pubblicazione del Traité du Triangle Arithmétique che parla del Triangolo di Tartaglia di Pascal nel 1654 (Soluzione del problema del Cavalier de Meré).
1657 Huygens pubblica il de ratiociniis in ludo alae e nel 1666 Leibniz la sua Dissertatio de arte combinatorica.
1713 Bernoulli enuncia La legge dei grandi numeri nel Ars conjectandi.
1718 De Moivre risolve il problema centrale della teoria della probabilità.
1763 Escono dei lavori di Bayes sulla concetto di Probabilità condizionata e alcune formule inerenti ad essa.
1809 Durante il suo studio degli errori di osservazione in astronomia, Gauss ritrova la curva che poi in futuro prenderà il suo nome.
1809 Laplace dimostra il teorema centrale limite.
Gli studi sulla probabilità vengono assiomatizzati solo intorno agli anni venti e trenta del 1900 con la pubblicazione di Kolmogorov. Si diffonderanno solo a partire dal 1933 con la pubblicazione della traduzione in tedesco dei Concetti fondamentali del Calcolo delle Probabilità (Grundbegriffe der Wahrscheinlichkeitsrechnung).
9. Dal problema del Cavalier De Meré a Daniel Kahneman
- Il calcolo delle probabilità è stata una delle più grandi scoperte della matematica.
La conoscenza del calcolo delle probabilità influenza la nostra vita quotidiana molto di più di quanto si possa immaginare.
- Ecco alcuni semplici affermazioni dietro le quali si scorge il contributo del calcolo delle probabilità:
- “Deve fare un esame di screening”
- “Quanto spendi per assicurare la tua automobile?”
- “Ti è arrivata la mia email?”
- “Lo vedo in forma. Vedrai che vince”
- · · ·
- In tutte queste circostanze la domanda o l’affermazione presuppone la valutazione della possibilità che un evento aleatorio si verifichi in un tempo futuro.
10. Innumeracy
In alcuni campi, come la medicina la psicologia, la conoscenza dei fondamenti del calcolo delle probabilità diventa una questione molto delicata. Il medico e lo psicologo, infatti, nella formulazione delle diagnosi si avvalgono della così detta “casistica”
che permette di determinare la probabilità dell’incidenza di un fenomeno.
Inoltre, sono categorie che nella loro attività professionale potrebbero dover essere tenuti a spiegare ad altri (i pazienti) il concetto di probabile (che si declina come rischio in questi contesti).
- Il matematico J. Allen Paulos, alla fine del secolo scorso, ha cercato di valutare il grado di difficoltà che si incontra nella apprezzamento del concetto di incertezza1.
- Le conclusioni a cui giunse Paulos furono piuttosto scoraggianti.
- La incapacità di ragionare correttamente sulle cose incerte è diffusa anche fra soggetti che hanno gradi di istruzione elevati.
1 Innumeracy, Vintage Books, New York, 1988
11. Cosa vuol dire Innumeracy?
Alcuni esempi di deduzioni errate
Affermazione: Il 70% dei consumatori abituali di eroina ha fatto uso di marijuana!
Deduzione: Il consumo di marijuana porta alla dipendenza dall’eroina nel 70% dei soggetti.
Affermazione: . . .sabato e domenica pioverà con probabilità del 50%.
Deduzione: Nel WE pioverà con probabilità del 100%.
Affermazione: Se una donna ha un cancro al seno, il suo mammogramma risulta positivo con probabilità del 90%.
Deduzione: In caso di mammogramma positivo la probabilità di avere un cancro al seno è del 90%.
G. Gigerenzer, Quando i numeri ingannano, Raffaello Cortina Editore, Milano, 2003
12. Il problema del Cavalier de Meré /1
Prima di procedere oltre nella formalizzazione dei concetti fondamentali del calcolo delle probabilità, soffermiamoci sul problema del Cavalier de Meré. Il modo con cui il problema fu affrontato e risolto, attraverso la corrispondenza epistolare fra Pascal e Fermat, gettò le basi del moderno calcolo delle probabilità, tant’è che la data di quella corrispondenza, anno 1654, viene indicata come la data in cui nasce il calcolo delle probabilità.
Il Cavalier de Meré
Il Cavalier de Meré era uomo molto colto e raffinato, assiduo frequentatore della corte del re Sole. Le sue conoscenze matematiche e la passione per il gioco d’azzardo stimolarono alcune considerazione sulla possibilità
di vincere al gioco.
Il problema
Esistevano due giochi di dadi la cui probabilità di vincere, secondo de Merè, erano uguali. Tuttavia, osservando e annotando l’esito di lunghe serie di giocate, si rese conto che in uno dei due giochi l’aspettativa di vincere era migliore per il giocatore. Non trovando una spiegazione per questa apparente incongruenza, de Merè decise di porre il problema a Pascal. Quest’ultimo, pur avendo intuito la soluzione, si rivolse a Fermat per avere conforto per la sua intuizione e aiuto per la formalizzazione matematica della stessa.
13. Il problema del Cavalier de Meré /2
I due giochi di dadi
Gioco 1: 4 lanci
Un giocatore lancia un dado per quattro volte e vince se nei quattro lanci realizza un sei.
Gioco 2: 24 lanci
Un giocatore lancia una coppia di dadi per ventiquattro volte e vince se nei ventiquattro lanci realizza una coppia di sei.
Valutazione di de Merè
Gioco 1: La probabilità di avere un ![]() in
un singolo lancio è 1/6, in quattro lanci 4(1/6) = 2/3.
in
un singolo lancio è 1/6, in quattro lanci 4(1/6) = 2/3.
Gioco 2: La probabilità di avere due ![]()
![]() in un singolo lancio è 1/36, in ventiquattro lanci 24(1/36) = 2/3.
in un singolo lancio è 1/36, in ventiquattro lanci 24(1/36) = 2/3.
14. Concetti primitivi
Prova
Esperimento aleatorio dall’esito incerto.
Esito
Risultato di una prova.
Probabilità
Misura dell’attitudine di un esito a manifestarsi.
15. Assiomi della probabilità
Spazio campionario
Consideriamo un esperimento aleatorio, dall’esito incerto. Assumiamo che il risultato del singolo esperimento non possa essere previsto con esattezza, ma si conosce l’insieme dei possibili esiti, \(\{\omega_1, \omega_2, \dots , \omega_n\}\), allora l’insieme di tutti i gli esiti possibili prende il nome di spazio campionario e lo indicheremo con \(\Omega\), se gli esiti sono necessari e incompatibili.
Definizioni:
necessari: gli esiti \(\{\omega_1, \omega_2, \dots , \omega_n\}\) si dicono necessari se rappresentano l’insieme esaustivo di tutti gli esiti possibili della prova. In altre parole uno di essi si dovrà verificare necessariamente.
incompatibili: il verificarsi di un esito esclude la possibilità che se ne verifichi anche un altro.
16. Spazio campionario
Esempio
Consideriamo l’esperimento che prevede come prova il lancio di un dado (non truccato o comunque ben bilanciato), l’insieme Ω = {1, 2, 3, 4, 5, 6} è uno spazio campionario poiché:
- il presentarsi di una faccia esclude la possibilità che se ne presenti un’altra;
- è impossibile che venga estratto un numero diverso da quelli indicati sulle sei facce del dado.
17. Esiti ed eventi
- Abbiamo indicato con esito l’elemento dello spazio campionario che si verifica come risultato della prova. L’insieme dei possibili esiti costituisce l’insieme \(\Omega\), lo spazio campionario.
- Riprendiamo l’esempio del lancio del dado. È possibile che la nostra attenzione sia rivolta non al singolo esito, ma a un insieme di esiti, per esempio siamo interessati a valutare come risultato della prova che esca un numero pari.
Combinazioni di esiti determinano partizioni dello spazio campionario e definiscono eventi. L’evento numero pari sarà definito dall’insieme degli esiti \(\mathsf{PARI} = \{2 \cup 4 \cup 6\}\). - Il simbolo \(\cup\) si legge unione.
- Analogamente possiamo definire l’evento numero minore o uguale a 3: \( \leq 3 = \{1 \cup 2 \cup 3\}\)
Eventi
D’ora in avanti parleremo, come risultato di una prova di evento e non più di esito assumendo che il generico evento \(E\) è un sottoinsieme dello spazio campionario \(\Omega\) e che, ovviamente, l’evento può essere associato anche ad un solo esito.
18. Unione e intersezione di eventi
evento favorevole: l’evento a cui rivolgiamo la nostra attenzione prende il nome di evento favorevole.
evento contrario: l’insieme degli eventi che non appartengono all’insieme dell’evento favorevole costituiscono l’evento contrario (o complementare).
- Indicheremo con \(E\) il generico evento favorevole e con \(\overline{E}\) (si legge “non \(E\)”) il generico evento contrario.
- Si ricava che:
\[\{E \cup \overline{E}\} = \Omega\]\[\{E \cap \overline{E}\} = \emptyset\] - dove l’operatore \(\cup\) si legge “o” e indica l’unione, pertanto l’evento \(E\) o \(\overline{E}\) non può che coincidere con \(\Omega\).
- dove l’operatore \(\cap\) si legge “e” e indica l’intersezione, pertanto l’evento \(E\) e \(\overline{E}\) identifica un insieme vuoto.
19. Notazioni
Terminologia
\(\color{brown}{\Omega}\) Spazio campionario o spazio degli eventi.
\(\color{brown}{\omega}\) Esito. L’esito è un generico elemento dell’insieme \(\Omega\).
\(\color{brown}{E}\) Evento favorevole (sottoinsieme dello spazio campionario). L’evento favorevole è il sottoinsieme di \(\Omega\) a cui è rivolta la nostra attenzione. Un evento può corrispondere ad un singolo esito o ad una combinazione di esiti. Indicheremo con \(E_i\) il generico evento.
\(\color{brown}{\overline{E}}\) Evento contrario (o complementare). L’evento contrario include tutti gli eventi in \(\Omega\) che non costituiscono l’evento favorevole \(E\).
\(\color{brown}{E_1 \cup E_2}\) Unione di eventi. L’evento \(E_{1,2} = (E_1 \cup E_2)\) è un evento definito dalla unione di \(E_1\) e \(E_2\). Diremo che \(E_{1,2}\) si verifica se si verifica \(E_1\) o \(E_2\) (cioè uno qualsiasi degli eventi che costituiscono \(E_{1,2}\).
Se ne deduce da ciò che: \(\{E \cup \overline{E}\} = \Omega\).
\(\color{brown}{E_1 \cap E_2}\) Intersezione di eventi. Il verificarsi dell’evento \((E_1 \cap E_2)\), invece, presuppone il verificarsi di \(E_1\) e \(E_2\).
\(\color{brown}{\emptyset}\) Insieme vuoto. È vuoto l’insieme costituito dall’intersezione \((E \cap \overline{E})\).
20. Esempi
Prova: lancio di un dado
\(\Omega\) \(\{\) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/1Nero.png" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/2Nero.png" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/3Nero.png" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/4Nero.png" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/5Nero.png" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/6Nero.png" alt="" width="18" height="18" role="presentation"> \(\}\), numeri naturali compresi nell’intervallo \([1, \dots , 6]\).
\(\omega\) Esito. La faccia è un generico esito, che corrisponde al numero \(4\).
\(E\) Evento favorevole semplice. Se l’evento favorevole è un evento semplice coincide con l’esito: \(E =\) ![]() \(= 4\).
\(= 4\).
Evento favorevole composto. È un insieme di esiti, per esempio, le
facce del dado che corrispondono ad un numero pari, \(E = \{\) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/2Nero.png?time=1619021357640" alt="" width="18" height="18" role="presentation"> ,
<img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/4Nero.png?time=1619021396848" alt="" width="18" height="18" role="presentation">, <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/6Nero.png?time=1619021418143" alt="" width="18" height="18" role="presentation"> \(\} = \{2, 4, 6\} \).
\(\overline{E}\) Evento contrario (o complementare). Se \(E = \{ \) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/2Nero.png?time=1619021357640" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/4Nero.png?time=1619021396848" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/6Nero.png?time=1619021418143" alt="" width="18" height="18" role="presentation"> \( \} \) allora \(\overline{E} = \{ \) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/1Nero.png" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/3Nero.png" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/5Nero.png" alt="" width="18" height="18" role="presentation"> \( \} \).
\(E_1 \cup E_2\) Unione di eventi. Sullo spazio campionario \(\Omega\) definiamo gli eventi:
1) Numero pari \(E_{\text{pari}} = \{\) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/2Nero.png?time=1619021357640" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/4Nero.png?time=1619021396848" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/6Nero.png?time=1619021418143" alt="" width="18" height="18" role="presentation"> \( \} = \{2, 4, 6\}\).
2) Numero \((> 3) \;\; E_{(>3)} = \{ \)
<img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/4Nero.png?time=1619021396848" alt="" width="18" height="18" role="presentation"> ,
<img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/5Nero.png" alt="" width="18" height="18" role="presentation">
, <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/6Nero.png?time=1619021418143" alt="" width="18" height="18" role="presentation">
\( \} = \{ 4, 5, 6 \}\).
L’evento \(E = \left( E_{\text{pari}} \cup E_ {(>3)} \right)\) è l’evento definito dalla unione di \(E_{\text{pari}}\) o \(E_{(>3)}\) e corrisponde a \(E = \{ \)
<img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/2Nero.png?time=1619021357640" alt="" width="18" height="18" role="presentation">, <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/4Nero.png?time=1619021396848" alt="" width="18" height="18" role="presentation">
, <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/5Nero.png" alt="" width="18" height="18" role="presentation">,
<img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/6Nero.png?time=1619021418143" alt="" width="18" height="18" role="presentation"> \( \} = \{2, 4, 5, 6\}\).
\(E_1 \cap E_2\) Intersezione di eventi. Sullo spazio campionario \(\Omega\) definiamo gli eventi:
1) Numero pari \(E_{\text{pari}} = \{\) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/2Nero.png?time=1619021357640" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/4Nero.png?time=1619021396848" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/6Nero.png?time=1619021418143" alt="" width="18" height="18" role="presentation"> \( \} = \{2, 4, 6\}\).
2) Numero \((> 3) \;\; E_{(>3)} = \{ \)
<img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/4Nero.png?time=1619021396848" alt="" width="18" height="18" role="presentation"> ,
<img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/5Nero.png" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/6Nero.png?time=1619021418143" alt="" width="18" height="18" role="presentation"> \( \} = \{ 4, 5, 6 \}\).
L’evento \(E = \left( E_{\text{pari}} \cap E_ {(>3)} \right)\) è l’evento definito dagli esiti che che appartengono sia all’evento \(E_{\text{pari}} \) e sia all’evento \(E_{(>3)}\) e corrisponde
a: \(E = \{\) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/4Nero.png?time=1619021396848" alt="" width="18" height="18" role="presentation"> , <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87093/6Nero.png?time=1619021418143" alt="" width="18" height="18" role="presentation"> \(\} = \{4, 6\}\).
21. Probabilità
Definizione
Una funzione \(P\) che assegna un numero reale \(P(E_i)\) a ciascun evento \(\{E_1, E_2, \dots , E_n\}\) di \(\Omega\) è una distribuzione di probabilità se soddisfa i tre seguenti assiomi (assiomi fondamentali del calcolo delle probabilità):
Assioma 1: \(P(E_i) \geq 0\) per qualsiasi \(E_i\) che appartiene ad \(\Omega\).
Assioma 2: \(P(\Omega) = \max\). \(\Omega\) rappresenta l’evento certo e quindi la sua probabilità è massima. Per convenzione si ha che \(\max(P) = 1 \) e quindi \(P(\Omega) = 1\).
Assioma 3: Siano \(\{E_1, E_2, \dots , E_n\}\) eventi disgiunti, non hanno esiti in comune, allora:
\[P(E_i \cup E_j) = P(E_i) + P(E_j), \text{ con } i \neq j \text{ e } \]
\[ \displaystyle P\left(\bigcup_{i=1}^n E_i \right) = \sum_{i=1}^n P(E_i) \]
22. Soggettivisti e Frequentisti /1
Esiste un lungo dibattito sulla valutazione della quantità \(P(E_i)\). In una estrema semplificazione (ma veramente estrema!!) la questione può essere banalizzata in questi termini.
- I soggettivisti (detti anche Bayesiani, in quanto ispirati al pensiero di Thomas Bayes) sostengono che è possibile utilizzare tutta la nostra conoscenza relativa all’esperimento aleatorio per determinare una regola che possa valutare \(P(E_i)\).
- I frequentisti sostengono che la nostra informazione riguardo \(P(E_i)\) si ricava dalla osservazione empirica. Solo ripetendo un numero (infinito) molto grande di volte l’esperimento, il rapporto fra i numero di casi favorevoli (casi in cui si è osservato l’evento \(E_i\)) e il numero totale delle prove si potrà determinare \(P(E_i)\).
23. Soggettivisti e Frequentisti /2
Riprendiamo l’esempio del dado (ben bilanciato),
Soggettivisti: Non è necessario ripetere l’esperimento un gran (infinito) numero di volte per stabilire che \(P(\)![]() \() = \frac{1}{6}\). In un dado ben bilanciato tutte le facce hanno la medesima attitudine a presentarsi.
\() = \frac{1}{6}\). In un dado ben bilanciato tutte le facce hanno la medesima attitudine a presentarsi.
Frequentisti: Solo ripetendo numerose (infinite) volte l’esperimento sarà possibile determinare la frequenza con cui ciascuna faccia si presenta. La probabilità si determina quando il rapporto fra casi favorevoli e numero di prove si stabilizza attorno ad un valore.
24. Eventi Indipendenti
Definizione
Due eventi \(A\) e \(B\) si dicono indipendenti se possiamo scrivere che
\[ P(A \cap B) = P(A) \times P(B) \]
La condizione di indipendenza fra eventi può essere determinata in diversi modi:
- Si assume esplicitamente che due eventi sono indipendenti. Lanciando due dadi non c’è ragione di ritenere che l’esito di uno possa influenzare l’esito dell’altro. In tal caso è possibile assumere esplicitamente che gli eventi sono indipendenti.
- Due eventi disgiunti \(A\) e \(B\) non sono indipendenti se \(P(A) \times P(B) > 0\) e allo stesso tempo se \(P(A \cap B) = P(\emptyset)\) allora \(P(A \cap B) = 0\).
25. Il problema del Cavalier de Meré - I due giochi dei dadi /1
Dove si sbagliava de Meré?
- Gli eventi associati a ciascun lancio sono indipendenti fra loro perché le prove sono indipendenti. In altre parole de Meré non aveva considerato che ogni prova è associata ad uno spazio campionario \(\Omega\) tale che \(P(\Omega) = 1\).
- Non è possibile sommare le probabilità associate ad eventi che appartengono a spazi campionari disgiunti.
Infatti, se nel primo gioco (ma si può fare lo stesso ragionamento anche per il secondo) i lanci fossero 6 e non 4, secondo il ragionamento di de Meré la probabilità di vincere è 1 o addirittura maggiore di 1 nel caso di più di 6 lanci. - Il ragionamento corretto presuppone la determinazione di uno spazio campionario congiunto che prevede tutte le possibili combinazioni nei 4 lanci assumendo che \(P(E = 6) = \frac{1}{6}\) è probabilità di vincita e \(P(\overline{E} \neq 6) = \frac{5}{6}\) e la probabilità di non vincere nella singola prova.
26. Il problema del Cavalier de Meré - I due giochi dei dadi /2
Soluzione Pascal/Fermat del problema 1
Il presupposto corretto per impostare il problema è considerare che l’esperimento aleatorio consiste di 4 prove indipendenti.
- Il giocatore lancia il dado, realizza un 6 e vince. La probabilità di vincere al primo lancio è quindi \(1/6\).
- Il giocatore non ha vinto al primo lancio, ma può sperare di vincere al secondo. La probabilità di non vincere al primo lancio è \(5/6\). Quindi: non vincere al primo e vincere al secondo è un evento con probabilità \((5/6)(1/6) = 5/36\).
- Situazione al terzo lancio \((5/6)(5/6)(1/6) = 25/216 \dots \)
\(\dots\) al quarto e ultimo caso \((5/6)(5/6)(5/6)(1/6) = 125/1296\).
Quindi \( \dfrac{1}{6} + \dfrac{5}{36} + \dfrac{25}{216} + \dfrac{}{} = 0,5178\) ,
che è un numero più piccolo di \(2/3\).
27. Il problema del Cavalier de Meré - I due giochi dei dadi /3
Soluzione Pascal/Fermat del problema 2
- Il giocatore lancia i dadi, realizza una coppia di 6 e vince. La probabilità di vincere al primo lancio è quindi \(1/36\).
- Il giocatore non ha vinto al primo lancio, ma può sperare di vincere al secondo. La probabilità di non vincere al primo lancio è \(35/36\). Quindi: non vincere al primo e vincere al secondo è un evento con probabilità \((35/36)(1/36) = 35/1296\).
\(\dots\)
- Poiché il giocatore ha 24 lanci a disposizione, la probabilità vincere al ventiquattresimo lancio è \(\left(\dfrac{35}{36}\right)^{23}\left(\dfrac{1}{36}\right) = 0,015\).
- Sviluppando i calcoli e sommando si avrà \(0,4914\), che è inferiore a \(2/3\), ma anche inferiore a \(0,5178\), come aveva intuito il de Merè.
28. Il problema del Cavalier de Meré - I due giochi dei dadi /4
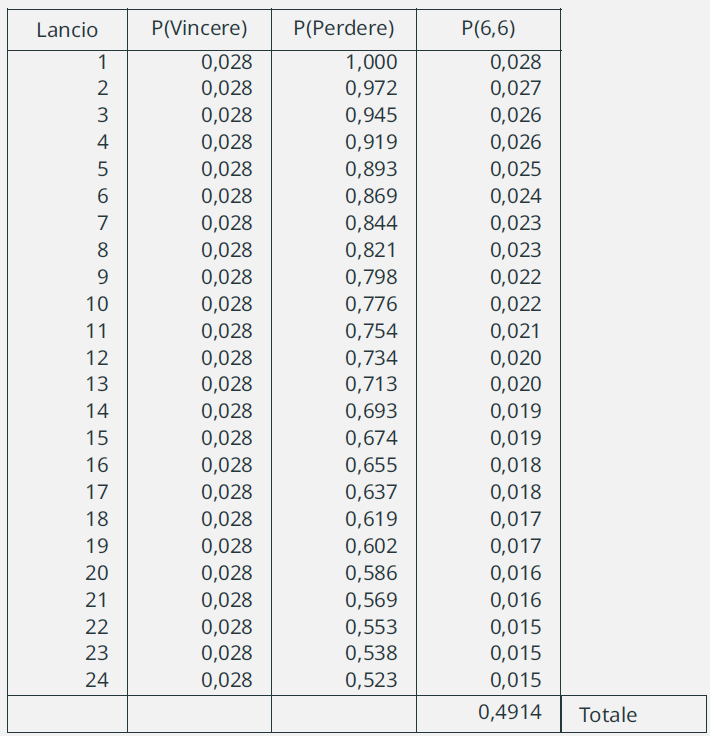
29. Il problema del Cavalier de Meré - I due giochi dei dadi /5
In realtà il problema del Cavalier Merè era un po’ più complicato della semplice determinazione della probabilità di vincita.
- Il gioco premiava la vittoria ripagando il giocatore con una vincita pari alla posta. In altre parole scommettendo un euro, in caso di vittoria si ricevevano due euro: la posta + la vincita.
- Un gioco equo (detto anche martingala) premia il giocatore di una quota della posta che è pari alla sua aspettativa di vincita.
- Scommettendo un Euro, il primo gioco dovrebbe ricevere circa 1, 931Euro in caso di vincita, mentre il secondo circa 2, 035.
- Poiché pagavano sempre 2 Euro, è chiaro che conveniva giocare al primo che riconosceva una vincita maggiore della vincita attesa di 1, 93.
- La domanda di De Meré era: poiché il giocatore ha la facoltà di ritirarsi dal gioco dopo un certo numero di lanci, in caso di ritiro come si deve dividere la posta?
- Il “Gioco dei pacchi” non è null’altro che la versione moderna e più spettacolare del gioco dei dadi di de Meré!
30. La teoria della probabilità
“La teoria della probabilità è, al fondo, semplice buon senso tradotto in calcolo... È degno di nota che questa scienza, nata al servizio dei giochi d’azzardo, sia diventata il più importante oggetto della conoscenza umana... Le più importanti questioni della vita sono, per la maggior parte, solo dei problemi di probabilità”
Laplace
31. Probabilità condizionata /1
Si assume che \(P(B) > 0\), la quantità \(P(A | B)\) indica la probabilità che si verifichi l’evento \(A\) sapendo che (dato che) si è già verificato l’evento \(B\).
Definizione
Se \(P(B) > 0\) allora la probabilità condizionata di \(A\) dato \(B\) è definita come:
\[P(A | B) = \dfrac{P(A \cap B)}{P(B)} \]
ovvero la probabilità dell’evento intersezione (\(A{\bf \text{ e }}B\)) diviso la probabilità dell’evento condizionante.
32. Probabilità condizionata /2
Prove dipendenti
Consideriamo l’esperimento lancio di un dado e definiamo di due seguenti spazi campionari:
- \(\Omega_1 = (\mathsf{PARI} ∪ \mathsf{DISPARI}) = \) \( \bigg( ( \)
 \(\cup\)
\(\cup\)
 \(\cup\)
\(\cup\)  \() \bigcup (\)
\() \bigcup (\)  \(\cup\)
\(\cup\)  \(\cup\)
\(\cup\)  \() \bigg) \)
\() \bigg) \)
- \(\Omega_2 = (\leq 3 \, \cup > 3) = \) \( \bigg( ( \)
 \(\cup\)
\(\cup\)
 \(\cup\)
\(\cup\)  \() \bigcup (\)
\() \bigcup (\)  \(\cup\)
\(\cup\)  \(\cup\)
\(\cup\)  \() \bigg) \)
\() \bigg) \)
- e consideriamo l’evento \(P(\mathsf{PARI} |> 3)\), i numeri pari e \(> 3\) sono il \(\bf 4\) e il \(\bf 6\), cioè 2 su 6, poiché assumiamo che è già noto che il numero è \(> 3\), allora lo spazio campionario si riduce solo a \((> 3) = \) e quindi il \(4\) e il \(6\) sono 2 su 3 possibili esiti. Si ricava quindi che:
\[ P(\mathsf{PARI}| >3) = \frac{P(\mathsf{PARI}\cap >3)}{P(>3)} = \frac{\frac{2}{6}}{\frac{3}{6}} = \frac{2}{\cancel{6}}\times \frac{\cancel{6}}{3}=\frac{2}{3}\]
33. Probabilità condizionata /3
Prove indipendenti
Consideriamo l’esperimento lancio di due dadi e definiamo i due seguenti spazi campionari indipendentemente: \(\Omega_1 \rightarrow\) primo lancio e \(\Omega_2 \rightarrow\) secondo lancio.
- \(\Omega_1 = (\mathsf{PARI} ∪ \mathsf{DISPARI}) = \) \( \bigg( ( \)
 \(\cup\)
\(\cup\)
 \(\cup\)
\(\cup\)  \() \bigcup (\)
\() \bigcup (\)  \(\cup\)
\(\cup\)  \(\cup\)
\(\cup\)  \() \bigg) \)
\() \bigg) \)
- \(\Omega_2 = (\leq 3 \, \cup > 3) = \) \( \bigg( ( \)
 \(\cup\)
\(\cup\)
 \(\cup\)
\(\cup\)  \() \bigcup (\)
\() \bigcup (\)  \(\cup\)
\(\cup\)  \(\cup\)
\(\cup\)  \() \bigg) \)
\() \bigg) \)
- e consideriamo l’evento \(P(\mathsf{PARI} |> 3) \). I numeri pari in \(\Omega_1\) sono \(\bf 2\), \(\bf 4\) e \(\bf 6\), cioè 3 su 6, quindi \(P(\mathsf{PARI}) = 0,5\). Parimenti si ha in \(\Omega_2 P(> 3) = 0,5\).
- Le prove sono indipendenti e quindi l’intersezione \(P(\mathsf{PARI}\cap > 3)\) è formata dalle seguenti combinazioni: \(\{4, 2\}, \{4, 4\},\{4, 6\}, \{5, 2\}, \{5, 4\}, \{5, 6\} \) e \( \{6, 2\}, \{6, 4\}, \{6, 6\},\) cioè 9 combinazione su 36 possibili.
34. Probabilità condizionata /4
Prove indipendenti
- Le prove sono indipendenti e quindi l’intersezione \(P(\mathsf{PARI}\cap > 3)\) è formata dalle seguenti combinazioni: \(\{4, 2\}, \{4, 4\}, \{4, 6\}, \{5, 2\}, \{5, 4\}, \{5, 6\}\) e \(\{6, 2\}, \{6, 4\}, \{6, 6\}\), cioè 9 combinazione su 36 possibili.
Si ricava quindi che:
\[ P(\mathsf{PARI}\mid >3) = \frac{P(\mathsf{PARI}\cap >3)}{P(>3)} = \frac{\frac{\cancel{9}^1}{\cancel{36}_4}}{\frac{\cancel{3}^{1}}{\cancel{6}_2}} = \frac{1}{4}\times\frac{2}{1}=\frac{1}{2}\]
- Allo stesso risultato si sarebbe giunti considerando che la probabilità associata all’evento intersezione di prove indipendenti è pari al prodotto delle probabilità:
\(P(\mathsf{PARI}\cap >3) = \frac{1}{2}\times\frac{1}{2} = \frac{1}{4}\), da cui si ricava:
\[P(\mathsf{PARI}\mid >3) = \frac{P(\mathsf{PARI}\cap >3)}{P(>3)} = \frac{1}{4}\times\frac{2}{1} = \frac{1}{2}.\]
35. Probabilità condizionata /5
Se A e B sono indipendenti il condizionamento non ha alcun effetto.
Lancio di due dadi: esempio
Assumiamo che la prova consiste nel lancio di due dadi. Il lancio di due dadi ha come spazio campionario:
\( \Omega = \big\{ (\) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87110/1Bianco.png" alt="" width="18" height="18" role="presentation"> \(;\) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87110/1Bianco.png?time=1618926561031" alt="" width="18" height="18" role="presentation"> \(),\) \( ( \) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87110/1Bianco.png?time=1618926735640" alt="" width="18" height="18" role="presentation"> \(;\) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87110/2Bianco.png" alt="" width="18" height="18" role="presentation"> \( ), \dots , ( \) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87110/5Bianco.png" alt="" width="18" height="18" role="presentation"> \( ; \) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87110/6Bianco.png" alt="" width="18" height="18" role="presentation"> \( ),\) \( ( \) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87110/6Bianco.png?time=1618926858621" alt="" width="18" height="18" role="presentation"> \( ; \) <img src="https://lms.federica.eu/pluginfile.php/306027/mod_book/chapter/87110/6Bianco.png?time=1618926877666" alt="" width="18" height="18" role="presentation"> \( ) \big\} \)
e i due eventi sono chiaramente indipendenti, pertanto la probabilità che si verifichi una qualsiasi coppia è pari a:
\( P( \) ![]() \(\cap\)
\(\cap\) ![]() \( ) = P( \)
\( ) = P( \) ![]() \( ) \times P( \)
\( ) \times P( \) ![]() \( ).\)
\( ).\)
Consideriamo il seguente condizionamento: \( P( \) ![]() \( | \)
\( | \) ![]() \( ).\)
\( ).\)
\( P( \) ![]() \( | \)
\( | \) ![]() \( ) = P( \)
\( ) = P( \) ![]() \(\cap\)
\(\cap\) ![]() \( ) / P(\)
\( ) / P(\) ![]() \( ) = P( \)
\( ) = P( \) ![]() \( ) \times P( \)
\( ) \times P( \) ![]() \( ) / P( \)
\( ) / P( \) ![]() \( ) = P( \)
\( ) = P( \) ![]() \( ) .\)
\( ) .\)
36. Teorema di Bayes /1
Legge della probabilità totale
Siano gli eventi \(A_1, A_2, \ldots. A_n\) una partizione di \(\Omega_A\) quindi
\[P(A_1 \cup A_2 \cup \cdots \cup A_n) = 1,\]
e sia \(B\) un generico evento dello spazio campionario \(\Omega_B\) tale che \(P(B) > 0\), si dimostra facilmente che
\[P(B) = \sum_{i=1}^{n} P(B\mid A_i)P(A_i)\]
infatti basta sostituire il generico termine \(P(B\mid A_i)\) con \(\displaystyle{\frac{P(B\cap A_i)}{P(A_i)}}\blacksquare\)
37. Teorema di Bayes /2
Definizione
Siano gli eventi \(A_1, A_2, \dots A_n\) una partizione di \(\Omega_A\), tali che \(P(A_i) > 0 \,\, \forall i\), se \(P(B) > 0\) allora si ha
\[P(A_i| B) = \dfrac{P(B | A_i)P(A_i)}{\sum_{i=1}^n P(B | A_i)P(A_i)}\]
Anche in questo caso la dimostrazione è immediata, basta considerare che:
- \(P(B | A_i)P(A_i) = P(B \cap A_i)\)
e che
- \(P(B) =\sum_{i=1}^n P(B | A_i)P(A_i)\) per la legge della probabilità totale.
38. Teorema di Bayes /3
In uno studio sulla relazione fra il grado di istruzione genitori/figli, sono stati estratti indipendentemente due gruppi di 100 soggetti di nati fra il 1980 e il 1982: laureati e non laureati. Hanno dichiarato di avere il padre laureato, rispettivamente,
38 laureati e 15 non laureati.
Sulla base dei dati ISTAT sappiamo che fra i nati negli anni ’80-82 il tasso di laureati è del 24,5%. Determinare la probabilità che il figlio sia laureato, posto che il padre (non) sia laureato.

39. Teorema di Bayes /4
Passiamo alla tabella delle probabilità empiriche e a margine indichiamo l’informazione aggiuntiva: \(P(\text{laurea}) = 0,245\).
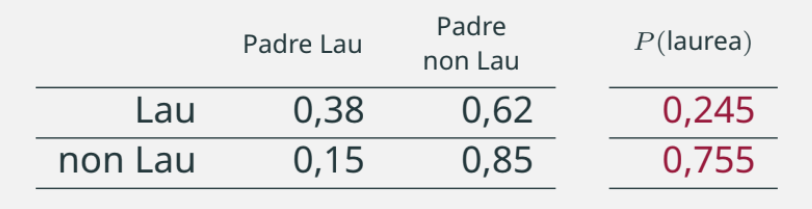
La probabilità \(P(\text{Padre Lau} | \text{Lau}) = 0,38\) si legge come: probabilità di aver un padre laureato dato che si possiede la laurea.
Allo stesso modo, \(P(\text{Padre non Lau} | \text{non Lau}) = 0,85\) e si legge come la probabilità di avere un padre non laureato dato che non si possiede la laurea.
40. Teorema di Bayes /5
Utilizzando l’informazione aggiuntiva, relativa alla probabilità di essere laureati nell’intera popolazione di riferimento, e ricordando che:
\[P(A | B) = \dfrac{P(A \cap B)}{P(B)}\]
possiamo ricavare le probabilità relative alle intersezioni come:
\(P(A \cap B) = P(A | B) \times P(B)\), quindi:
\[P(\text{Padre Lau} \cap \text{Lau}) = P(\text{Padre Lau } | \text{ Lau}) \times P(\text{Lau})\]
\[P(\text{Padre Lau} \cap \text{Lau}) = 0,38 \times 0,245 = 0,093\]
41. Teorema di Bayes /6
La distribuzione congiunta sarà quindi:
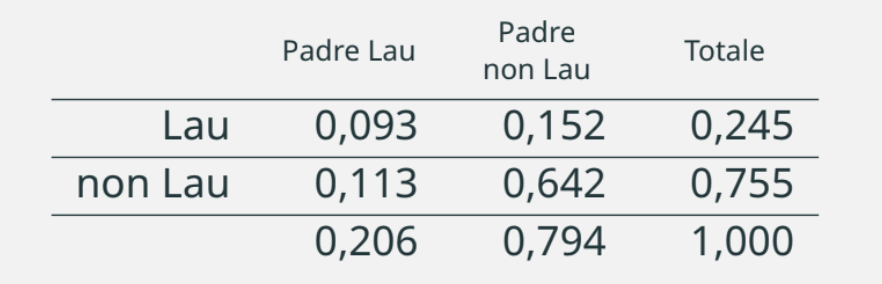
A questo punto punto è possibile calcolare la distribuzione marginale relativa alla Laurea Padre.
La probabilità di estrarre un soggetto che ha la laurea, dato che il padre sia laureato, si determina attraverso il seguente condizionamento:
\[P(\text{Lau } | \text{ Padre Lau}) = \dfrac{0,093}{0,206} = 0,451 \, .\]
E’ interessante notare come questa probabilità sia molto più grande di
\[P(\text{Lau } | \text{ Padre non Lau}) = 0,191 \, .\]
42. Il problema di Monty Hall /1
 |
 |
 |
|---|
Monty Hall è un conduttore televisivo americano divenuto famoso per il gioco delle tre porte.
Durante il gioco, Monty Hall presenta tre porte ad un concorrente e gli chiede di sceglierne una spendo che dietro una di essa c’è un’auto di lusso, dietro un’altra una capra e niente dietro la terza.
43. Il problema di Monty Hall /2
 |
 |
 |
|---|---|---|
 |
|
La probabilità di vincere scegliendo una porta caso è \(\dfrac{1}{3}\).
Il concorrente sceglie una porta a caso.
44. Il problema di Monty Hall /3
 |
 |
 |
|---|---|---|
 |
|
Monty Hall, che sa dov’è la capra e dov’è l’automobile, apre la porta scelta se il concorrente ha vinto, altrimenti apre la porta vuota. A questo punto chiede al concorrente se intende mantenere la sua scelta o vuole cambiare porta.
Cosa deve fare il concorrente?
45. Il problema di Monty Hall /4
 |
 |
 |
|---|
Il concorrente deve cambiare per aumentare la sua probabilità di vincere. Perché?
46. Il problema di Monty Hall /5
 |
 |
 |
|---|---|---|
 |
 |
 |
Inizialmente la probabilità è distribuita secondo una distribuzione uniforme rispetto alle tre opzioni (porte). Il concorrente, quindi, non può far meglio di scegliere a caso una delle tre porte.
47. Il problema di Monty Hall /6
 |
 |
 |
|---|---|---|
 |
 |
 |
 |
|
48. Il problema di Monty Hall /7
 |
 |
 |
|---|---|---|
 |
 |
 |
 |
|
Monty Hall apre la porta sapendo che dietro non c’è nulla. Questo, quindi non è un evento aleatorio, ma determina un cambio dello spazio campionario (Cambio di variabile nella versione italiana del film 21).
49. Il problema di Monty Hall /8
 |
 |
 |
|---|---|---|
 |
  |
 |
 |
|
La scelta migliore, quindi, consiste e chiedere di cambiare porta, determinando un raddoppio della probabilità di vincere.
50. Il problema di Monty Hall /9
 |
 |
 |
|---|---|---|
 |
  |
 |
 |
|
51. Il problema di Monty Hall /10
 |
 |
 |
|---|---|---|
 |
  |
 |
 |
|
52. Variabili casuali (v.c.) /1
Una variabile casuale è una applicazione di \(\Omega\) in \(\mathbb{R}\):
\[X : \Omega \rightarrow \mathbb{R}\]
dove \(\mathbb{R}\) indica l’insieme dei numeri reali.
- Una variabile casuale non è altro che una regola che assegna a ciascun elemento dello spazio campionario un elemento di \(\mathbb{R}\).
- Se \(\Omega\) è un insieme (al più) numerabile allora \(X(E_i)\) è una v.c. discreta (o categorica), per \(E_i\) ∈ \(\Omega\).
- Se \(\Omega\) è un insieme non numerabile allora \(X(E_i)\) è una v.c. continua, per \(E_i \in\Omega\) e \(E_i \subset\mathbb{R}\).
- Poiché l’insieme \(\mathbb{R}\) è per definizione un insieme ordinato, la funzione delle probabilità cumulate (o di ripartizione) associata alla v.c. \(X\) è una funzione definita in \(\mathbb{R}\) tale che \(F(x) \rightarrow [0; 1], ∀x ∈ X\).
53. Funzioni di distribuzione di probabilità
Definizione
Sia \(X\) una variabile casuale discreta, si definisce funzione di distribuzione delle probabilità per \(X\) la funzione \(f(x_i) = P(X = x_i)\).
Dalla precedente definizione si ricava che:
- \(f(x_i) \geq 0\) per un insieme al più numerabile di \(x_1, x_2, \dots , x_n\);
- \(f(x_i) = 0\) altrove;
- \(f(x_i) = P(X = x_i) \equiv P(E_i)\), con \(i = 1, 2, \dots , n\);
- \(\displaystyle\sum_{i=1}^n f(x_i) = 1\).
54. Funzioni di densità di probabilità
Definizione
Sia \(X\) una variabile casuale continua, si definisce funzione di densità delle probabilità la funzione \(f(x)\) tale che:
- \(f(x) \geq 0 \; \forall x\)
- \(\displaystyle\int_{-\infty}^{+\infty} f(x)\mathrm{d}x = 1\)
- \(P(a < X < b) = \displaystyle\int_a^b f(x)\mathrm{d}x\), con \(a \leq b\)
Dalla precedente definizione si ricava che:
- \(F(X = a) = \displaystyle\int_{-\infty}^a f(x)\mathrm{d}x = P(X \leq a)\);
- \(f(x) = F'(X)\) in tutti i punti in cui \(F(x)\) è differenziabile;
la funzione di densità di probabilità equivale alla derivata prima della funzione di ripartizione \(F(x)\).
55. Valore atteso e Varianza di una v.c. /1
Il valore atteso1 di una variabile casuale può essere interpretato come una sorta di media della v.c., ed in certi casi lo è. Nel caso di v.c. discrete, il valore atteso non è altro che la sommatoria dei prodotti di ciascuna \(X = x_i\) ponderata per la probabilità corrispondente \(P(X = x_i)\). Nel caso continuo, non potendo utilizzare l’operatore di sommatoria dobbiamo ricorrere al calcolo integrale, ma il concetto resta lo stesso.
Caso continuo
\[ \mu = E[X] = \int_{-\infty}^{+\infty} xf(x)\mathrm{d}x \]
Caso discreto
\[ \mu = E[X] = \sum_{j=1}^N x_jP(X = x_j) \]
1Il valore atteso è detto anche Speranza Matematica.
56. Valore atteso e Varianza di una v.c. /2
La varianza è una misura di variabilità definita come la media degli scarti al quadrato rispetto alla media:
Caso continuo
\[\sigma^2 = E[(X − \mu)^2] = \displaystyle\int_{-\infty}^{+\infty} (x − \mu)^2f(x)\mathrm{d}x \]
Con poca difficoltà si può dimostrare che \(E[(X − \mu)^2] = E[X^2] − \mu^2\).
Caso discreto
\[\sigma^2 = E[(X − \mu)^2] = \sum_{j=1}^N (x_j − \mu)^2 P(X = x_j) \]
57. Momenti v.c.
Sia \(X\) una generica variabile casuale, la quantità
\[m^r = \int_{-\infty}^{\infty}x^r f(x) \mathrm{d}x\]
si definisce momento di ordine \(r\).
Analogamente, la quantità
\[ m^r = \int_{-\infty}^{\infty}(x-\mu)^r f(x) \mathrm{d}x \]
si definisce momento centrato di ordine \(r\).
Se ne deduce che:
- la media è il momento di ordine \(1\)
- la varianza è il momento centrato di ordine \(2\) e che può essere definita come la differenza fra il momento di ordine 2 (\( \int_{-\infty}^{\infty}x^2 f(x) \mathrm{d}x\)) ed il quadrato del momento di ordine \(1\):
\[\sigma^2 = \int_{-\infty}^{\infty}(x)^2 f(x) \mathrm{d}x - \mu^2 \]
o analogamente
\[\sigma^2=E[X^2]-\mu^2 \]
58. Funzioni di distribuzione di probabilità
Sia \(\Omega\) uno spazio campionario finito ed equiprobabile (tutti gli eventi hanno eguale probabilità), la v.c. \(X\) associata ad \(\Omega\) prende il nome di variabile casuale Uniforme discreta e sarà indicata con la notazione \(X \sim U\{\text{min}, \text{max}\}\).
Esempio
L’esempio più tipico di v.c. Uniforme discreta è quello relativo all’esperimento del lancio di un dado.
La v.c. \(X\) associata all’esperimento lancio di un dado è definita come \(X \sim U\{1, 6\}\) e la corrispondente funzione di distribuzione delle probabilità è:
\[\begin{array}{rcll} f(X=x_i) &=& \dfrac{1}{6}, & \quad \forall x_i\in \{1, 6\}\\[3pt] f(X) &=& 0 & \quad \text{altrove}. \end{array} \]
59. Funzioni di ripartizione o delle probabilità cumulate
Definizione
La funzione di ripartizione è la funzione \(F_X : \mathbb{R} \rightarrow [0, 1]\) definita come:
\[F(X = x_i) = P(X \leq x_i)\]
È una funzione monotona e non decrescente tale che:
\[ \lim_{x\to -\infty} F_X(x) = 0 \quad \text{ e } \quad \lim_{x\to +\infty} F_X(x) = 1 \]
\(F_X\) per \(X \sim U\{1, 6\}\)
\[\begin{array}{rcll} F(X=x_i) & = & i\times 1/6 & \forall x_i\in\{1,6\} \\[3pt] F_x & = & 0 & \text{if } X<1 \\[3pt] F_x & = & 1 & \text{if } X\geq 1 \end{array}\]
60. v.c. di Bernulli /1
Si consideri un esperimento aleatorio che prevede solo due possibili esiti: favorevole (F) e contrario (C). L’esempio più classico, ma anche il più astratto, è quello del lancio della moneta, che prevede solo due possibili esiti: Testa/Croce.
In realtà, a pensarci bene, durante una qualsiasi giornata si verificano un’enorme quantità di esperimenti bernulliani. Eccone una breve lista: mi sveglio con/senza il raffreddore, arrivo in ufficio in orario/ritardo, nasce un bambino maschio/femmina ecc..
\(\boldsymbol{X \sim B(\pi)}\)
Se assegnamo il valore \(1\) all’evento F e il valore \(0\) all’evento
C e attribuiamo la probabilità \(\boldsymbol{\pi}\) ad F, diremo che \(X \sim B(\pi)\) si distribuisce secondo v.c. di Bernulli a parametro \(\pi\) (il simbolo \(\boldsymbol{\sim}\) si legge “si distribuisce”).
\[\begin{array}{l} P(X = 1) = \pi \\[3pt] P(X = 0) = 1 − \pi \end{array} \quad,\]
che può essere scritta nella forma
\[f(x) = \pi^x (1 − \pi)^{1−x}, \quad \text{con } x \in \{0, 1\}.\]
61. v.c. di Bernulli /2
Se \(X\) è una generica variabile casuale, diremo che \(X\) è una variabile discreta se è definita sull’insieme dei numeri naturali \(\mathbb{N}\), se invece \(X\) è una v.c. continua avrà come supporto l’insieme \(\mathbb{R}\) dei numeri reali o un suo
sottoinsieme.
La v.c. di Bernulli è una particolare v.c. discreta che viene detta anche binaria o dicotomica. Se \(X\) si distribuisce secondo una v.c. di Bernulli, allora scriveremo che
\[X \sim B(\boldsymbol{\pi})\]
e leggiamo "\(X\) si distribuisce secondo una v.c. di Bernulli a parametro \(\pi\)".
In generale utilizzeremo sempre questa notazione, dove "\(\sim\)" si legge "si distribuisce secondo", il nome della v.c. viene abbreviato secondo una notazione condivisa da tutti (\(B\) per la Bernulli) e viene seguito dal o dai parametri fra parentesi tonde.
62. Valore atteso e varianza della v.c. di Bernulli /1
Le distribuzioni delle probabilità si possono interpretare utilizzando gli stessi criteri delle distribuzioni delle frequenze relative. In fondo la frequenza relativa può essere considerata una probabilità empirica se \(n\), il numero delle prove, è grande
abbastanza.
Secondo la concezione frequentista, "grande abbastanza" indica che un incremento del numero di prove influenza in modo del tutto trascurabile le probabilità empiriche.
Assumiamo aver eseguito \(1000\) lanci di una moneta e di aver ottenuto \(482\) volte testa. Indichiamo con \(\hat{p}\) la probabilità empirica associata a testa, pertanto \(\hat{p} = 0,4820\).
Se eseguiamo un ulteriore lancio e osserviamo testa (ma sarebbe indifferente se assumessimo croce), la probabilità empirica associata diventa: \((482 + 1)/1001 = 0,4825\). Man mano che il denominatore aumenta (cioè aumenta il numero delle prove eseguite) il quoziente fra eventi favorevole e prove si modificherà in misura sempre minore.
63. Valore atteso e varianza della v.c. di Bernulli /2
Sia \(X\) una generica v.c. di Bernulli a parametro \(\pi\), indichiamo con \(E[X]\) il suo valore atteso che sarà definito come la somma del valore di \(X\) moltiplicato per la probabilità dell’evento corrispondente.
Abbiamo visto che:
- \(X = 1\) se l’evento è F, mentre \(X = 0\) nel caso di C;
- \(P(X = 1) = \pi\) e \(P(X = 0) = (1 − \pi)\)
Valore atteso di \(X\)
\[E[X] = 1\times\pi + 0\times (1-\pi) = \color{brown}{\pi}\]
Varianza di \(X\)
\[ \begin{aligned} E[(X - \pi)^2] &= (1-\pi)^2\times\pi + (0 - \pi)^2\times(1-\pi) = \\ &=(1- 2\times\pi + \pi^2)\times\pi + \pi^2\times(1-\pi) =\\ &= \pi -2\times\pi^2 + \bcancel{\pi^3} + \pi^2 - \bcancel{\pi^3} = \color{brown}{\pi\times(1-\pi)}. \end{aligned} \]
Analogamente, ricordando che la varianza è definibile anche come la differenza fra il momento secondo e il quadrato del momento primo si ha:
\[ \begin{aligned} E[(X - \pi)^2] & = (1^2\pi + 0^2(1 - \pi)) - \pi^2 \\[3pt] & = \pi - \pi^2 \\[3pt] & = \pi(1-\pi). \end{aligned} \]
64. v.c. Binomiale /1
Si consideri una serie di \(n\) prove bernulliane identiche (\(\pi\) costante) e indipendenti, per cui possiamo scrivere che la probabilità di avere \(n\) eventi favorevoli in \(n\) prove sarà
\[P(F \cap F \cap \dots \cap F) = \pi^n \, .\]
Se, assumiamo che in \(n\) prove bernulliane si possono verificare \(x\) eventi favorevoli e \((n − x)\) eventi contrari bisogna considerare tutte le possibili combinazioni degli \(x\) eventi favorevoli su \(n\) posizioni. Se non si vuol tenere conto dell’ordine, ma solo del numero di eventi favorevoli sulle \(n\) prove bisogna valutare il numero di combinazioni "equivalenti"
\(n = 5\) e \(x = 3\)
Dodici combinazioni “equivalenti”:
\[11100, 11010, 11001, 10110, 10101, 10011, 01110, 01010, 01011, 00111\]
65. v.c. Binomiale /2
Definizione
Si consideri un esperimento aleatorio che consiste in n prove bernulliane i.i. (identiche e indipendenti) a parametro \(\pi\), si dirà che \(X \sim Bin(n\pi)\) (\(X\) si distribuisce secondo una v.c. Binomiale con parametri \(n\) e \(\pi\)) se lo spazio campionario è costituito dal numero di successi che si possono verificare in \(n\) prove indipendenti (o bernulliane), senza tenere conto dell’ordine della sequenza.
Il coefficiente binomiale
Per determinare il numero di sequenze bisogna fare ricorso al calcolo combinatorio.
Il numero di combinazioni di \(n\) elementi presi ‘a \(x\) a \(x\)’ è definito dalla seguente espressione:
\[ \binom{n}{x} = \dfrac{n!}{(n − x)! \times x!} \]
dove \(n!\) (si legge: “\(n\) fattoriale”) è dato da
\[ n! = n \times (n − 1) \times (n − 2) \times \dots \times 1 \]
66. v.c. Binomiale /3
È molto semplice capire la logica del coefficiente binomiale.
Assumiamo che \(n = 5\) e \(x = 3\) e indichiamo i tre eventi favorevoli con \(F_1, F_2, F_3\) e i due eventi contrari con \(C_1\) e \(C_2\), ricordiamo che non teniamo conto dell’ordine.
Se le prove sono \(n = 5\), allora le combinazioni senza ripetizione sono \(5 \times 4 \times 3 \times 2 \times 1 = 120\), ma poiché consideriamo uguali gli eventi che si differenziano solo per permutazioni fra gli \(F\) e i \(C\), es. \(F_1, F_2,
F_3, C_1, C_2\) e \(F_2, F_3, F_1, C_2, C_1,\) bisogna dividere \(120\) per \(12\).
Si osservi, infatti, che i tre esiti \(F\) si possono combinare fra loro in \(6\) modi diversi (\(3 \times 2\)) e i due esiti \(C\) in due modi, complessivamente in \(12\) modi diversi, infatti \((3 \times 2 \times 1) * (2 \times 1) = 12\).
67. v.c. Binomiale /3
Esempio
Consideriamo il caso in cui \(n = 5\) e \(X = 3\), dove \(X\) sta ad indicare una generica v.c. Binomiale con \(n = 5\) e \(\pi\) qualsiasi.
Gli eventi sono ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; 1 e 2 sono eventi favorevoli, gli altri tre sono eventi contrari. Poiché la variabile casuale tiene
conto delle combinazioni ma non delle disposizioni, gli eventi (
; 1 e 2 sono eventi favorevoli, gli altri tre sono eventi contrari. Poiché la variabile casuale tiene
conto delle combinazioni ma non delle disposizioni, gli eventi ( ![]() ,
, ![]() ) e (
) e ( ![]() ,
, ![]() ) sono da considerarsi equivalenti. In quanti modi si possono combinare i \(5\) eventi? Poiché le prove sono \(5\), l’evento
) sono da considerarsi equivalenti. In quanti modi si possono combinare i \(5\) eventi? Poiché le prove sono \(5\), l’evento ![]() alla prima prova ha \(5\) posizioni disponibili. Il secondo evento può occupare
una delle quattro posizioni libere, il terzo ha tre opzioni ha disposizione, il quarto due e l’ultimo, il quinto, potrà occupare solo l’ultima posizione.
alla prima prova ha \(5\) posizioni disponibili. Il secondo evento può occupare
una delle quattro posizioni libere, il terzo ha tre opzioni ha disposizione, il quarto due e l’ultimo, il quinto, potrà occupare solo l’ultima posizione.
Riassumendo: le posizioni disponibili sono \(5\) per il primo, \(5 \times 4\) per il
primo e il secondo, \(5 \times 4 \times 3\) per i primi tre e \(\color{brown}{5 \times 4 \times 3 \times 2 = 5! = 120}\) per tutti e cinque.
68. v.c. Binomiale /4
Esempio
Poiché è irrilevante come si combinano fra loro gli eventi favorevoli e i contrari, si avrà che le permutazioni:
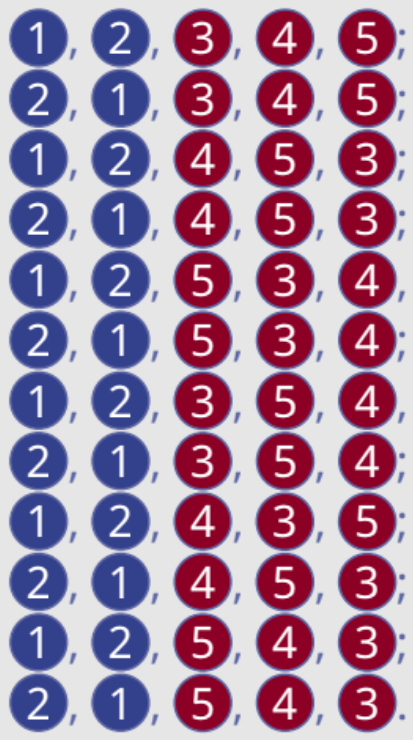
devono essere considerate una sola volta. Si osservi che il totale delle permutazioni, considerando i due eventi insieme è dato da
\[(3 \times 2 \times 1) \times (2 \times 1) = 3! \times 2! = 12\]
69. v.c. Binomiale /5
Esempio
Lo stesso vale per la combinazione ( ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ) che, come per la configurazione precedente, definisce \(6 \times 2 = 12\) permutazioni di cui non si deve tener conto:
) che, come per la configurazione precedente, definisce \(6 \times 2 = 12\) permutazioni di cui non si deve tener conto:
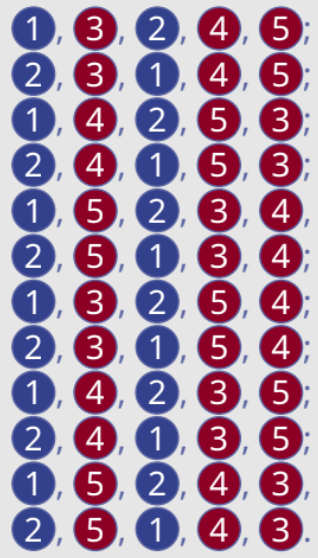
e così via!
70. v.c. Binomiale /6
Definizione
La v.c. \(X\) si definisce Binomiale, e si indica con la notazione \(X \sim Bin(n, \pi)\) se lo spazio campionario è definito da numero di successi che si possono ottenere in \(n\) prove bernulliane a parametro costante \(\pi\). La funzione di distribuzione di probabilità corrispondente, che indichiamo con \(f(x | n, \pi)\), esprime la quantità \(P(X = x), (\forall x \in \{1, 2, 3, \dots, n\})\), cioè esprime la probabilità che su \(n\) prove bernulliane si verifichino \(x\) eventi favorevoli, indipendentemente dall’ordine con cui si presentano. Formalmente, la sua funzione di distribuzione di probabilità è
\[f(x) = \dfrac{n!}{x! \times (n − x)!} \times \pi^x \times (1 − \pi)^{(n−x)}\]
Valore atteso e varianza
Avendo definito la v.c. Binomiale come una somma di v.c. di Bernulli possiamo ricavare il valore atteso e la varianza come somma del valore atteso (proprietà della media) e della varianza (proprietà della varianzaa) della Bernulli, pertanto
- \(E[X] = n \times \pi\)
- \(E[(X − E[X])^2] = n \times \pi \times (1 − \pi)\)
aSe le prove sono eseguite sotto la condizione di indipendenza e il parametro \(\pi\)
è costante, la varianza totale si può esprimere come somma delle varianze.