Unit 2 - Verifica di ipotesi
| Site: | Federica Web Learning - LMS |
| Course: | Statistica Psicometrica |
| Unit: | Unit 2 - Verifica di ipotesi |
| Printed by: | Utente ospite |
| Date: | Wednesday, 17 December 2025, 4:52 AM |
Table of contents
- 1. Verifica di ipotesi /1
- 2. Verifica di ipotesi /2
- 3. Verifica di ipotesi dalla distribuzione Normale
- 4. L'ipotesi alternativa
- 5. Test sulla media sotto la condizione \(\sigma^2\) noto /1
- 6. Test sulla media sotto la condizione \(\sigma^2\) noto /2
- 7. Test sulla media sotto la condizione \(\sigma^2\) noto /3
- 8. Test sulla media sotto la condizione \(\sigma^2\) noto /4
- 9. Errore di decisione /1
- 10. Errore di decisione /2
- 11. Test su medie sotto la condizione \(\sigma_1 = \sigma_2\) e \(\sigma\) noto /1
- 12. Test su medie sotto la condizione \(\sigma_1=\sigma_2\) e \(\sigma\) noto /2
- 13. Test su medie sotto la condizione \(\sigma_1=\sigma_2\) e \(\sigma\) noto /3
- 14. Il test su medie per \(X\sim N\) e \(\sigma^2\) non noto
- 15. Distribuzione chi-quadrato \(\chi^2\) /1
- 16. Distribuzione chi-quadrato \(\chi^2\) /2
- 17. La varianza campionaria \(\hat{S}^2\) /1
- 18. La varianza campionaria \(\hat{S}^2\) /2
- 19. La varianza campionaria \(\hat{S}^2\) /3
- 20. v.c. \(t\) di Student
- 21. Distribuzione di \(t\) di Student
- 22. Test delle medie con varianze incognite e omogenee /1
- 23. Test delle medie con varianze incognite e omogenee /2
- 24. Test delle medie con varianze incognite e omogenee /3
- 25. Test delle medie con varianze incognite e omogenee /4
- 26. Test delle medie con varianze incognite e omogenee /5
1. Verifica di ipotesi /1
- Il processo di verifica di ipotesi in statistica è un approccio filosofico rispetto ad un processo decisionale.
- La verifica di ipotesi consente di assumere decisioni in condizioni di incertezza potendo fissare apriori la probabilità di assumere una decisione errata.
- Una ipotesi statistica è una asserzione o supposizione sulla distribuzione di una o più variabili casuali.
- Se l'ipotesi specifica completamente la distribuzione si dice semplice; in caso contrario si chiama composta.
- Per denotare una ipotesi statistica useremo il carattere H : seguito dai due punti, seguiti a loro volta dall'asserzione che specifica l'ipotesi.
- Se l'ipotesi è formulata su un parametro della popolazione allora si parla di verifica parametrica.
2. Verifica di ipotesi /2
Test per una ipotesi statistica
Un test di una ipotesi statistica \(H\) è una regola per decidere se rifiutare o meno \(H\).
Rifiutando \(H\) si stabilisce che il campione su cui abbiamo determinato la statistica test non proviene dalla popolazione che abbiamo assunto essere vera.
Poiché la decisione viene assunta sulla base di una variabile casuale (la statistica test) si è consapevoli del rischio di commettere un errore.
La “potenza” del metodo è nel fatto che la probabilità di commettere un errore può essere controllata fissando una soglia prima ancora di effettuare il test.
3. Verifica di ipotesi dalla distribuzione Normale
Assumiamo che:
- \(\mathcal{X}\) è un generico carattere continuo che si connota secondo la distribuzione normale all'interno della popolazione
- la variabile \(X\), quindi si distribuisce normalmente
- la distribuzione dipende dai parametri \(\mu\) e \(\sigma\) e assumiamo che \(\sigma\) sia noto (non può modificarsi)
Si assume come vera l'ipotesi:
\[ H_0 : \mu = k \]
dove \(k\) è una qualsiasi costante.
L'ipotesi che viene assunta come vera viene indicata con \(H_0\) e chiamata anche ipotesi nulla.
4. L'ipotesi alternativa
Se l’ipotesi nulla non è vera, bisogna immaginare in che modo possa essere intervenuto un cambiamento nella popolazione.
- la media è pari ad un valore \(k'\) dove \(k \neq k' : H_1 : \mu = k'\)
- la media è maggiore di \(k\) dove: \(H_1 : \mu > k\)
- la media è minore di \(k\) dove: \(H_1 : \mu < k\)
- la media è diversa da \(k: H_1 :\neq< k\)
è molto importante scegliere l’ipotesi alternativa più corretta.
- \(H_1 : \mu = k'\) ipotesi alternativa semplice (1 valore)
- \(H_1 : \mu > k\) ipotesi alternativa complessa a destra (unidirezionale)
- \(H_1 : \mu < k\) ipotesi alternativa complessa a sinistra (unidirezionale)
- \(H_1 : \mu \neq k\) ipotesi alternativa complessa (bidirezionale)
5. Test sulla media sotto la condizione \(\sigma^2\) noto /1
Le ipotesi
Assumiamo che \(X\) sia una generica v.c. con varianza nota pari a \(\sigma^2\) e che \(n > 30\) oppure che \(X \sim N(\mu, \sigma^2)\).
Sotto queste condizioni sappiamo che \(\bar{X}_{(n)} \approx N(\mu, \sigma^2/n)\) nel primo caso e \(\bar{X}_{(n)} \sim N(\mu, \sigma^2/n)\) nel secondo caso.
Si vuole porre a verifica l’ipotesi nulla \(H_0 : \mu = k\) contro una delle seguenti ipotesi alternative
semplice \(H_1 : \mu = c\), dove \(c \neq k\)
complessa unidirezionale \(H_1 : \mu > k\) (unidirezionale a destra),
\(H_1 : \mu < k\) (unidirezionale a sinistra)
complessa bidirezionale \(H_1 : \mu \neq k\)
Ricordiamo che \(\approx\) si legge si approssima e \(\sim\) sta a indicare si distribuisce.
6. Test sulla media sotto la condizione \(\sigma^2\) noto /2
La statistica test
Il parametro \(\mu\) sul quale intendiamo prendere la nostra decisione è una quantità incognita. Sappiamo che la media campionaria \(\bar{X}\) è una funzione (stimatore) in grado di dare buone informazioni rispetto a \(\mu\). Infatti, sotto le condizioni che abbiamo assunto, la media del nostro campione di ampiezza \(n\) sarà una determinazione di una v.c. Normale con varianza nota e pari a \(\sigma^2/n\).
Il livello di significatività ed errore di I tipo
Assumendo che \(H_0\) sia vera, a causa dell'errore di campionamento, è molto improbabile che \(\bar{x} = k\). Pertanto prima di eseguire il test (estrarre il campione) dobbiamo decidere fino a che punto siamo disposti ad imputare la differenza \(\bar{x} \neq k\) all'errore di campionamento e assumere \(H_0\) come vera, piuttosto che ritenere che la differenza sia da imputare al fatto che \(H_0\) è falsa?
Osserviamo che l'intero ragionamento è sviluppato solo rispetto ad \(H_0\) perché è la sola ipotesi che possiamo "specificare" avendo assunto note la distribuzione e i suoi parametri: \(\mu=k\) e \(\sigma^2\) noto.
7. Test sulla media sotto la condizione \(\sigma^2\) noto /3
Il livello di significatività
Il rischio che siamo disposti a correre affermando che \(H_0\) è falsa, quando essa in realtà è vera, prende il nome di livello di significatività e corrisponde ad una probabilità scelta dal ricercatore e da individuare sotto \(H_0\).
La probabilità corrisponde ad una porzione di area sotto la curva che descrive la distribuzione della statistica test. La logica vuole che, dato un livello di significatività (un'area), la “regione di rifiuto” abbia la massima estensione possibile.
Ciò impone che la regione di rifiuto debba essere individuata nelle code della distribuzione.
\(\boldsymbol{\alpha}\)
Il livello di significatività viene universalmente indicato con \(\color{brown}{\alpha}\) e nelle scienze umane è in generale fissato su uno dei seguenti valori \(0.1, 0.05 , 0.01\). Si tende a preferire \(0,05\).
8. Test sulla media sotto la condizione \(\sigma^2\) noto /4
L’errore di II tipo
Può accadere, tuttavia, che sulla base di alpha si decida di non rifiutare \(H_0\) e decidere di conseguenza che \(H_0\) è vera. Non abbiamo nessuna certezza che la decisone presa sia corretta poichè la nostra statistica test \(\bar{x}\) potrebbe essere stata generata sotto una condizione diversa da quella descritta sotto \(H_0\) (addirittura potrebbe essere cambiata anche \(\sigma^2\) rispetto alle ipotesi formulate e che, sempre per l’errore di campionamento, la differenza fra \(\bar{x}\) e \(k\) non è stata tale farci rifiutare \(H_0\).
In questo caso sarà stato commesso un errore di II tipo.
9. Errore di decisione /1
Il test si concluderà in una di queste quattro condizioni:
- \(H_0\) è vera
decisione corretta accettare \(H_0\)
decisione errata rifiutare \(H_0\) Errore di I tipo (o specie)
- \(H_0\) è falsa
decisione corretta rifiutare \(H_0\)
decisione errata accettare \(H_0\) Errore di II tipo (o specie)
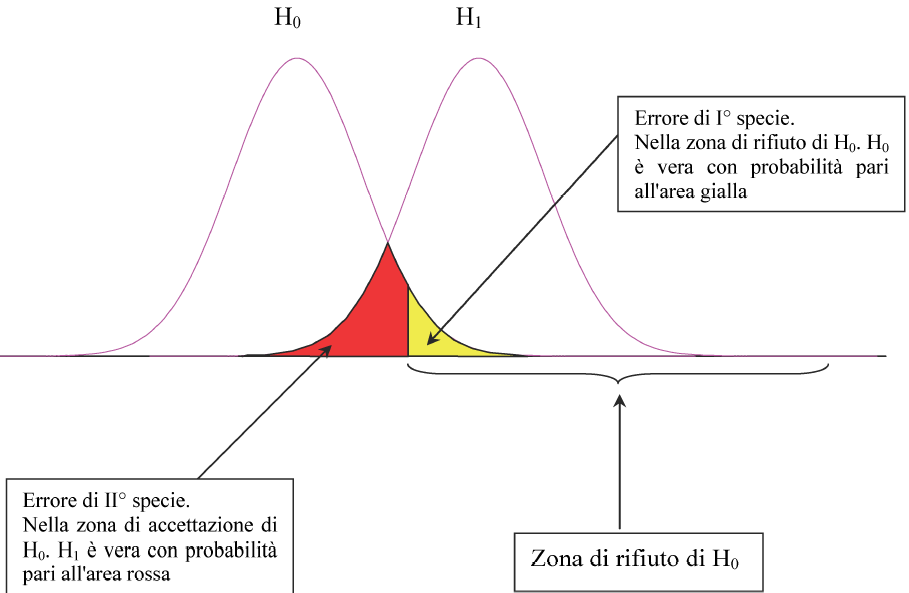
10. Errore di decisione /2
La statistica test è:
\[ \color{brown}{\boxed{Z= \dfrac{\bar{X}-k}{\sqrt{\frac{\sigma^2}{n}}} \sim N(0,1)}} \]
Utilizzando il valore standardizzato della media del nostro campione x ̄, determinazione della media campionaria \(\bar{X} \sim N(0, \sigma^2)\) sotto \(H_0\), riconduciamo il test ad una forma standardizzata di più facile e immediata interpretazione
ed eseguibile con il solo uso della tavola.
Tuttavia, disponendo di un software in grado di calcolare i quantili per qualsiasi coppia di parametri \(\mu\) e \(\sigma^2\) della normale, possiamo eseguire il test con varianza nota anche senza standardizzare.
11. Test su medie sotto la condizione \(\sigma_1 = \sigma_2\) e \(\sigma\) noto /1
Siano \(X_1, X_2, \dots , X_{n_1}\) e \(X_1, X_2, \dots , X_{n_2}\) due campioni indipendenti rispettivamente di ampiezza \(n_1\) e \(n_2\) e che il carattere \(X\) si connota secondo una distribuzione normale.
Si vuole verificare l'ipotesi nulla \(\color{brown}{H_0 : \mu_1 = \mu_2}\) contro l'ipotesi alternativa \(\color{brown}{H_0 : \mu_1 \neq \mu_2}\) sotto la condizione \(\sigma_1 = \sigma_2\). In altre parole, quindi, se \(H_0\) è vera vuol dire che i due campioni provengono dalla medesima popolazione e la variabile \(X\) è tale che \(X \sim N(\mu, \sigma^2)\); se è vera \(H_1\) le popolazioni da cui provengono i campioni si differenziano solo per il valore medio \(\mu\).
Osserviamo che \(H_0\) può essere riscritta come \(\color{brown}{H_0 : \mu_1 − \mu_2 = 0}\), ovvero come la differenza fra medie (se la differenza è \(0\) le medie sono uguali).
12. Test su medie sotto la condizione \(\sigma_1=\sigma_2\) e \(\sigma\) noto /2
\(\boldsymbol{H_0: \mu_1 - \mu_2 = 0}\) contro \(\boldsymbol{H_1: \mu_1 - \mu_2 \neq 0}\)
Per la verifica di \(H_0\) utilizziamo le medie campionarie \(\bar{X}_1\) e \(\bar{X}_2\). Sotto \(H_0\) abbiamo che
\[ \bar{X}_1 \sim N\left(\mu, \frac{\sigma^2}{n_1}\right) \]
\[ \bar{X}_2 \sim N\left(\mu, \frac{\sigma^2}{n_2}\right) \]
da cui abbiamo che la statistica test è
\[ \displaystyle{\frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{\sigma^2}{n_1} + \frac{\sigma^2}{n_2}}}} \]
Avendo assunto che i campioni sono indipendenti e che le varianze sono uguali, possiamo definire la statistica test attraverso la somma delle variabili casuali \(\bar{X}_1\) e \(\bar{X}_2\), (\(\bar{X}_1-\bar{X}_2\) algebricamente è una somma!).
Ricordiamo che la somma di v.c. normali è ancora una normale e che sotto la condizione di indipendenza la varianza è espressa dalla somma delle varianze, quindi
\[ \displaystyle{\frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\sigma^2\left(\frac{1}{n_1} + \frac{1}{n_2}\right)}} \sim N(0,1)} \]
13. Test su medie sotto la condizione \(\sigma_1=\sigma_2\) e \(\sigma\) noto /3
Distribuzione di \(\boldsymbol{X}\) non normale e teorema del limite centrale
Nel caso in cui la distribuzione della variabile \(X\) non può essere assunta come normale e sotto l'ipotesi che la varianza è nota e che i campioni sono indipendenti, il teorema del limite centrale consente di stabilire che per \(n\geq 30\), se la distribuzione di \(X\) è simmetrica o moderatamente asimmetrica, possiamo ragionevolmente assumere che sotto \(H_0: \mu = k\), con \(k\) generica costante, la statistica campionaria
\[\frac{\bar{X}-k}{\sqrt{\frac{\sigma^2}{n}}} \approx N(0,1)\]
Analogamente, nel caso di due campioni indipendenti con ipotesi nulla \(H_0: \mu_1 - \mu_2 = 0\), sotto la condizione di varianze omogenee abbiamo
\[\displaystyle{\frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\sigma^2\left(\frac{1}{n_1} + \frac{1}{n_2}\right)}} \approx N(0,1)}\]
Sotto le stesse ipotesi, se \(n_1 = n_2\), si avrà
\[ \displaystyle{\frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{2\sigma^2}{n}}} \approx N(0,1)} \]
14. Il test su medie per \(X\sim N\) e \(\sigma^2\) non noto
Sotto le condizioni \(X\sim N(\mu,\sigma^2)\) con \(\sigma^2\) non è noto, il test statistico sulla media presuppone il ricorso ad una stima di \(\sigma^2\) a partire da uno stimatore che goda delle proprietà desiderabili per uno stimatore (possibilmente il miglior stimatore).
Il test \(\boldsymbol{t}\)
Dato un campione di ampiezza \(n\) consideriamo le seguenti ipotesi nulla e alternativa
\(H_0: \mu=k\)
\(H_1: \mu \neq k\) (o altra ipotesi unidirezionale o semplice)
Abbiamo visto che il miglior stimatore di \(\sigma^2\) è la varianza campionaria \(\hat{S}^2\) e pertanto a partire da questo possiamo ottenere la stima \(\hat{s}^2\) per \(\sigma^2\) e scrivere la statistica test standardizzata come
\[ \frac{\bar{X} - \mu}{\sqrt{\frac{\hat{S}^2}{n}}} \equiv \frac{\bar{X} - \mu}{\sqrt{\frac{S^2}{n-1}}} \]
Come si distribuisce questa quantità? È il rapporto fra due v.c. e quindi è anche essa una v.c. e per capire come si distribuisce è necessario capire come si distribuisce \(\hat{S}^2_{(n)}\).
15. Distribuzione chi-quadrato \(\chi^2\) /1
Il ruolo della distribuzione normale
Se \(X\sim N(\mu, \sigma^2)\) è possibile ricavare le distribuzioni campionarie di molte statistiche. Il nostro interesse si focalizza sulla distribuzione della v.c. \(\hat{S}^2\) varianza campionaria.
Cominciamo introducendo la v.c. \(\chi^2\) e la sua distribuzione. La distribuzione del chi-quadrato è un caso particolare della distribuzione \(\Gamma\), che noi non tratteremo. Ci limitiamo ad alcuni risultati fondamentali:
- la distribuzione del chi-quadrato \(\chi^2_n\) è definibile anche come la somma di v.c. normali standardizzate ed indipendenti
\[ \chi^2_n = \sum_{i=1}^{n}{Z_i^2} \] - la distribuzione del chi-quadrato è caratterizzata da un solo parametro \(n\) che prende il nome di gradi di libertà (d.f. degrees of freedom)
- se \(X \sim \chi^2_n \rightarrow \mathrm{E}[X] = n\);
- \(\mathrm{E}[(X - n)^2] = \mathrm{VAR}(X) = 2n\).
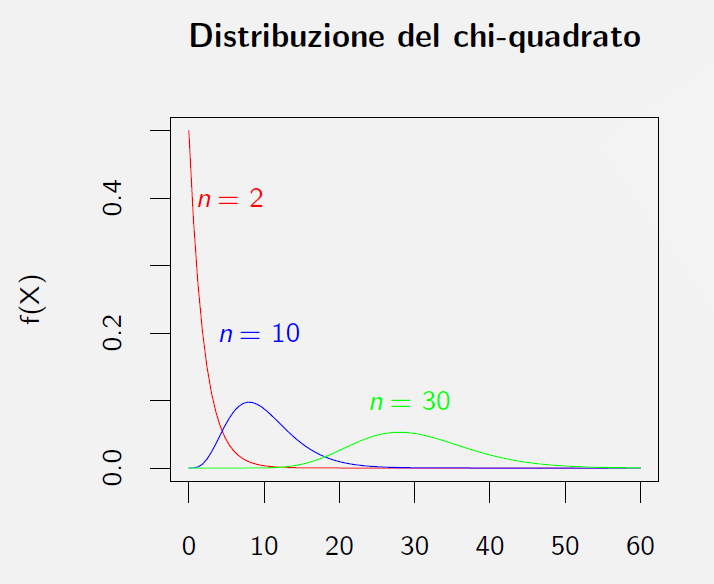
16. Distribuzione chi-quadrato \(\chi^2\) /2
Esempi di distribuzione \(\chi^2\) per \(n=2\), \(n=10\), \(n=30\)
17. La varianza campionaria \(\hat{S}^2\) /1
Riprendiamo lo stimatore di \(\sigma^2\) varianza campionaria ricordando che:
\[ \hat{S}^2 = \frac{1}{n-1}\sum_{i=1}^{n}{(X_i - \bar{X})^2} \]
da cui, aggiungendo e sottraendo \(\mu\) e passando alla formula ridotta per il calcolo della varianza avremo:
\[ \begin{eqnarray*} \hat{S}^2 &=& \frac{1}{n-1}\sum_{i=1}^{n}{[(X_i -\mu) - (\bar{X} - \mu)]^2} = \cr &=& \frac{1}{n-1}\sum_{i=1}^{n}{(X_i -\mu)^2 - \frac{n}{n-1}(\bar{X} - \mu)^2}, \end{eqnarray*}\]
da cui, dividendo tutto per \(\sigma^2\) e moltiplicando per \((n-1)\), si ha:
\[ \frac{(n-1)}{\sigma^2}\hat{S}^2 = \sum_{i=1}^{n}{\left(\frac{X_i -\mu}{\sigma}\right)^2} - n\left(\frac{\bar{X} - \mu}{\sigma}\right)^2 \]
18. La varianza campionaria \(\hat{S}^2\) /2
Riprendiamo la precedente:
\[ \frac{(n-1)}{\sigma^2}\hat{S}^2 = \sum_{i=1}^{n}{\left(\frac{X_i -\mu}{\sigma}\right)^2} - n\left(\frac{\bar{X} - \mu}{\sigma}\right)^2. \]
Osserviamo che, se \(X\sim N(\mu, \sigma^2)\), allora:
- \(\color{brown}{\displaystyle{\left(\frac{X_i -\mu}{\sigma}\right)}\sim N(0,1)}\)
- \(\color{brown}{\displaystyle{\frac{\sqrt{n}}{\sigma}(\bar{X} -\mu)}\sim N(0,1)}\)
da cui si ricava che:
\[ \frac{(n-1)}{\sigma^2}\hat{S}^2 \sim \chi^2_{n-1} \]
Infatti la quantità a sinistra della eq. in alto è la somma di \(n\( v.c. \(N(0,1)\) al quadrato meno un'altra \(N(0,1)\) sempre al quadrato. Poiché anche la v.c. \(\chi^2\) gode della proprietà della riproduttività rispetto alla somma, si avrà che \(\color{brown}{\chi^2_{n} - \chi^2_{1} = \chi^2_{(n-1)}}\).
19. La varianza campionaria \(\hat{S}^2\) /3
Utilizzando il risultato:
\[ \frac{(n-1)}{\sigma^2}\hat{S}^2 \sim \chi^2_{n-1} \]
è possibile definire gli intervalli di confidenza (intervalli di fiducia) utilizzando la distribuzione tabulata dell \(\chi^2_n\).
Assumiamo \(n=10\) e che \(X\sim N(\mu, \sigma^2)\). Utilizzando la tavola della \(\chi^2_9\) per \(n-1=9\)
g.d.l troviamo che il quinto e il novantacinquesimo percentile della distribuzione sono rispettivamente \(3,32\) e \(16.91\). L'intervallo di confidenza con probabilità pari \(0,9\) per \(\hat{S}^2_{(9)}\) è:
\[ \mathrm{P}\left(3,32 < 9\frac{\hat{S}^2_{(n)}}{\sigma^2} < 16,91\right) = 0,9 \]
da cui
\[ \mathrm{P}\left(\frac{9\hat{S}^2_{9}}{3,32} > \sigma^2 > \frac{9\hat{S}_{9}^2}{16,91}\right) = 0,9 \]
20. v.c. \(t\) di Student
Altra distribuzione campionaria fondamentale dell'inferenza statistica è quella associata alla v.c. \(t\) di Student. Definiamo la v.c. \(t_{(g.d.l.)}\) di Student come il rapporto fra una v.c. Normale standard e la radice quadrata di una v.c. chi-quadrato rapportata ai propri g.d.l., indipendenti fra di loro. La v.c. così definita avrà come unico parametro i g.d.l. della v.c. \(\chi^2\) posta al denominatore.
\[ \frac{\frac{(X - \mu)}{\sigma}}{\sqrt{\frac{\chi^2_{n}}{n-1}}} \sim t_{(n-1)} \]
Media campionaria con \(\sigma^2\) incognito
Consideriamo le v.c. \(\bar{X}\) e \(\hat{S}^2\), ricordando che la varianza di \(\bar{X}\) è \(\frac{\sigma^2}{n}\) e che \(\hat{S}^2 = \frac{n}{n-1}S^2\), definiamo l'errore standard come
\[ \color{brown}{\boxed{\mathrm{ES}_{\bar{X}} = \frac{1}{\sqrt{n-1}}S = \frac{1}{\sqrt{n}}\hat{S}}}, \]
passiamo alla standardizzata della \(\bar{X}\):
\[ \frac{\bar{X} - \mu}{\sqrt{\frac{S^2_{n}}{n-1}}} \sim t_{(n-1)}, \]
per dimostrare che è effettivamente una \(t\) di Student basta dividere numeratore e denominatore per la quantità incognita \(\frac{\sigma}{\sqrt{n}}\):
\[ \frac{\frac{\sqrt{n}(\bar{X} - \mu)}{\sigma}}{\sqrt{\frac{nS^2_{n}}{\sigma^{2}(n-1)}}} \sim t_{(n-1)} .\]
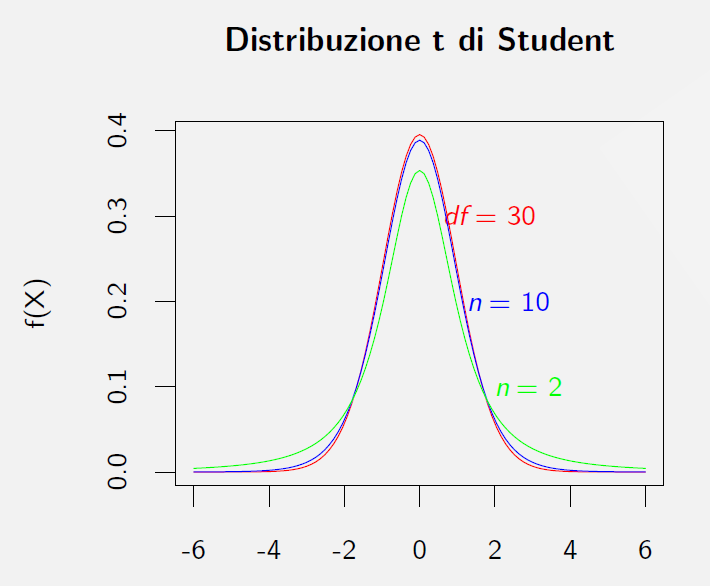
21. Distribuzione di \(t\) di Student
Esempi di distribuzione \(t\) di Student per \(n=2\), \(n=10\), \(n=30\)
22. Test delle medie con varianze incognite e omogenee /1
Data una variabile \(X\) per la quale è possibile assumere la distribuzione secondo una normale con varianza incognita e due campioni indipendenti di ampiezza \(n_1\) e \(n_2\), si vuole verificare l'ipotesi \(\color{brown}{H_0: \mu_1 - \mu_2 = 0}\) contro l'ipotesi alternativa \(\color{brown}{H_1: \mu_1 - \mu_2\neq 0}\).
Se \(\sigma\) fosse noto utilizzeremmo la statistica test
\[\color{brown}{\displaystyle{\frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\sigma^2\left(\frac{1}{n_1} + \frac{1}{n_2}\right)}} \sim N(0,1)}}.\]
Poiché \(\sigma\) è incognito usiamo il miglior stimatore che abbiamo per \(\sigma\) utilizzando lo stimatore
\[\hat{S}^2_{n_1 + n_2- 2 } = \frac{n_1 S^2_1 + n_2S^2_2}{n_1 + n_2 -2} = \frac{(n_1 -1)\hat{S}^2_1 + (n_2 -1)\hat{S}^2_2}{n_1 + n_2 -2}.\]
Questo stimatore è detto varianza campionaria congiunta.
23. Test delle medie con varianze incognite e omogenee /2
\[\hat{S}^2_{n_1 + n_2- 2 } = \frac{(n_1 -1)\hat{S}^2_1 + (n_2 -1)\hat{S}^2_2}{n_1 + n_2 -2}. \]
Avendo assunto che \(X \sim N\), allora
\[\frac{(n_1-1)\hat{S}^2_1}{\sigma^2} \sim \chi^2_{n_1-1}\]
e
\[\frac{(n_2-1)\hat{S}^2_2}{\sigma^2} \sim \chi^2_{n_2-1}.\]
Di conseguenza
\[\frac{1}{\sigma^2} \left[ (n_1-1)\hat{S}^2_1 + (n_2-1)\hat{S}^2_2\right] \sim \chi^2_{n_1+n_2-2}.\]
24. Test delle medie con varianze incognite e omogenee /3
Data una variabile \(X\) per la quale è possibile assumere la distribuzione secondo una normale con varianza incognita e due campioni indipendenti di ampiezza \(n_1\) e \(n_2\), si vuole verificare l'ipotesi \(\color{brown}{H_0: \mu_1 - \mu_2 = 0}\) contro l'ipotesi alternativa \(\color{brown}{H_1: \mu_1 - \mu_2\neq 0}\).
Sostituendo \(\sigma\) con lo stimatore nella statistica test si avrà
\[ \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\color{brown}{\frac{(n_1-1)\hat{S}^2_1 + (n_2-1)\hat{S}^2_2}{n_1+n_2-2}}\left(\frac{1}{n_1} + \frac{1}{n_2}\right)}} \sim t_{n_1+n_2-2}.\]
Nel caso di \(n_1 = n_2\) la precedente si semplifica in
\[\frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\color{brown}{\frac{\hat{S}^2_1 + \hat{S}^2_2}{n}}}} = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\color{brown}{\frac{S^2_1 + S^2_2}{n-1}}}}\sim t_{n_1+n_2-2}.\]
25. Test delle medie con varianze incognite e omogenee /4
Abbiamo visto che la distribuzione \(t\) di Student consente di fare inferenza sul parametro \(\mu\) di una di una generica variabile \(X\sim N(\mu, \sigma^2)\) dove \(\sigma^2\) è incognita. In particolare abbiamo dimostrato che la distribuzione \(t\) permette di porre a verifica mediante test statistico le seguenti ipotesi \(H_0\):
- \(\color{brown}{H_0: \mu = c}\) contro \(H_1: \mu \neq c\), dove \(c\) è una costante generica e \(H_1: \mu < c\), \(H_1: \mu > c\) e \(H_1: \mu = c^\prime\) sono casi particolari;
- \(\color{brown}{H_0: \mu_1 - \mu_2 = 0}\) contro \(H_1: \mu_1 - \mu_2 \neq 0\)
Nel caso del test sulla differenza di medie, sotto le ipotesi di campioni indipendenti, la statistica test è
\[t_{n_1+n_2 -2} = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{(n_1 -1 )\hat{S}_1^2 + (n_2 - 1)\hat{S}_2^2}{n_1+n_2 -2}\left(\frac{1}{n_1} + \frac{1}{n_2}\right) } } \]
La distribuzione \(\chi^2\) gode della proprietà della riproduttività. Il numeratore del denominatore \((n_1 -1 )\hat{S}_1^2 + (n_2 - 1)\hat{S}_2^2\) sarà ancora una distribuzione \(\chi^2\) se la \(X_1\) e la \(X_2\) sono omogenee rispetto alla varianza: \(\color{brown}{\sigma_1^2 = \sigma^2_2 = \sigma^2}\), si dice sono omoscedastiche o omogenee rispetto a \(\sigma^2\).
26. Test delle medie con varianze incognite e omogenee /5
Riprendiamo il test sulla differenza fra medie e assumiamo \(\bar{X}_1\) e \(\bar{X}_2\) sono v.c. indipendenti e omoscedastiche (\(\sigma_1^2 = \sigma^2_2\)) quindi sotto \(H_0\) si avrà che sono i.i.d.. Se \(n_1=n_2=n\) valgono le seguenti condizioni:
- \(\displaystyle{\mathrm{Var}(\bar{X}_1) = \mathrm{Var}(\bar{X}_2) = \frac{\sigma^2}{n}}\)
- \(\displaystyle{\mathrm{Var}(\bar{X}_1 -\bar{X}_2) = 2 \frac{\sigma^2}{n}}\)
da cui ricaviamo che:
\[ t_{n_1+n_2-2} = \frac{\frac{\sqrt{n}\bar{X}_1}{\sigma} - \frac{\sqrt{n}\bar{X}_2}{\sigma}}{\sqrt{\left(\frac{n(n-1)\hat{S}_1^2}{\sigma^2} + \frac{n(n-1)\hat{S}_2^2}{\sigma^2}\right)\frac{1}{n+n-2}}}\]
\[ t_{n_1+n_2-2} = \frac{\sqrt{\frac{n}{\sigma^2}}\left(\bar{X}_1 - \bar{X}_2 \right)}{\sqrt{\frac{n}{\sigma^2}}\sqrt{\frac{(n-1)\hat{S}_1^2 + (n-1)\hat{S}_2^2}{n+n-2}}} = \frac{\left(\bar{X}_1 - \bar{X}_2 \right)}{\sqrt{\frac{(n-1)\hat{S}_1^2 + (n-1)\hat{S}_2^2}{n+n-2}}}\]
E' da notare che solo assumendo \(\sigma_1^2 = \sigma_2^2\) è possibile sommare al denominatore e semplificare.