Unit 3 - v.c. F di Fisher
| Sito: | Federica Web Learning - LMS |
| Corso: | Statistica Psicometrica |
| Unit: | Unit 3 - v.c. F di Fisher |
| Stampato da: | Utente ospite |
| Data: | martedì, 3 marzo 2026, 06:26 |
1. v.c. \(F\) di Fisher /1
Introduciamo una nuova v.c., la \(F\) di Fisher. Siano \(U_{gl_1}\) e \(V_{gl_2}\) due v.c. \(\chi^2\) indipendenti con \(gl_1\) e \(gl_2\) gradi di libertà, rispettivamente, allora
\[F_{(gl_1, gl_2)} = \frac{\frac{U_{gl_1}}{gl_1}}{\frac{V_{gl_2}}{gl_2}} = \frac{U_{gl_1}}{V_{gl_2}}\frac{gl_2}{gl_1}\]
il rapporto fra due v.c. \(\chi^2\), ciascuna rapportata ai propri gradi di libertà definisce una v.c. con distribuzione \(F\) di Fisher e con gradi di libertà delle due v.c. \(\chi^2\) che la definiscono.
La \(F\) di Fisher è definita solo per \(x>0\) e varia in funzione dei gdl delle \(\chi^2\) che la definiscono.
2. v.c. \(F\) di Fisher /2
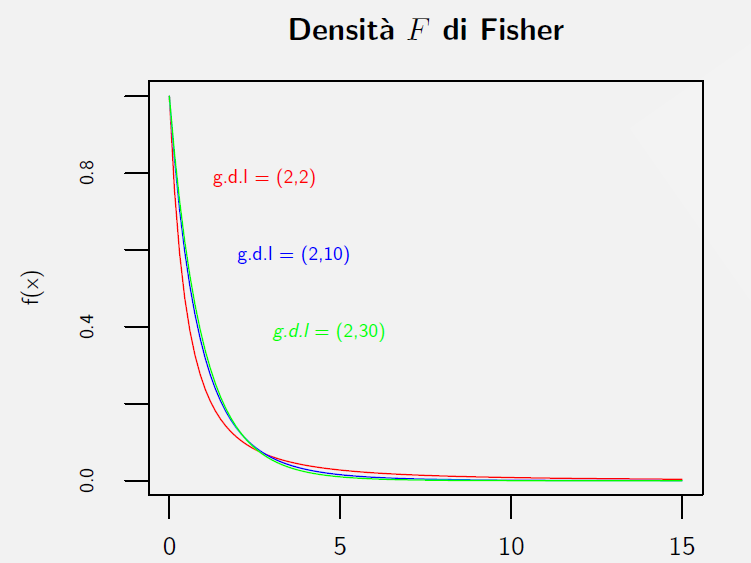
Esempi di distribuzione \(F\) di Fisher per \(gl_1=\{2\}\) e \(gl_2=\{\color{red}{2}, \color{blue}{10}, \color{green}{30}\}\)
3. v.c. \(F\) di Fisher /3
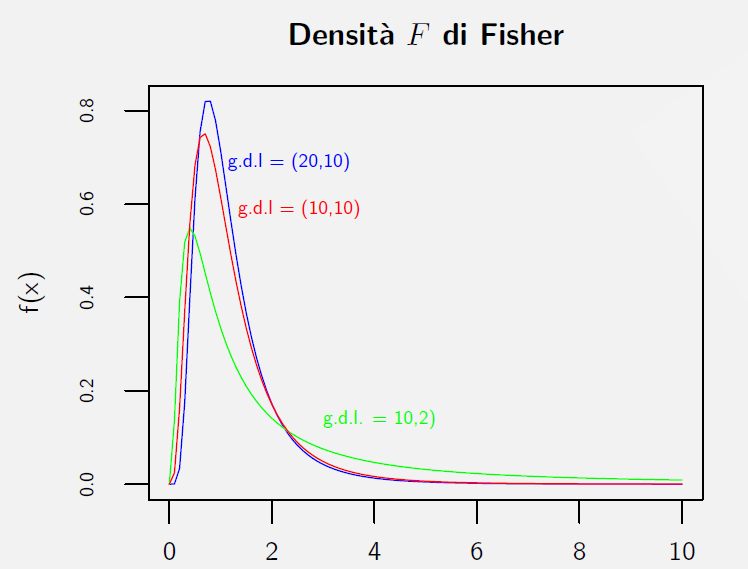
Esempi di distribuzione \(F\) di Fisher per \(\{gl_1,gl_2\}= \color{red} {(10,10)}, \color{blue}{(20,10)}, \color{green}{(10,2)}\)
4. Test sull'omogeneità delle varianze /1
Abbiamo visto che per determinare la varianza campionaria congiunta sotto la condizione \(H_0\) è necessario assumere campioni indipendenti (in modo che la varianza totale può essere determinata come somma delle varianze) e varianze omogenee.
Per verificare se è possibile accettare l'ipotesi che le varianze \(\sigma^2_1\) e \(\sigma^2_2\) sono omogenee è possibile procedere attraverso un test statistico. Esistono vari tipi di test per verificare questa ipotesi. Sicuramente, il più utilizzato
(anche per la sua semplicità) è il test sulla omogeneità delle varianze.
La statistica test è determinata attraverso il seguente rapporto
\[ F_{(n_1-1,n_2-1)} = \frac{\sum_{i=1}^{n_1}(X_{i1} - \bar{X}_1)^2}{\sigma^2(n_1-1)}\times \frac{\sigma^2(n_2-1)}{\sum_{i=1}^{n_2}(X_{i2} - \bar{X}_2)^2} = \frac{\hat{S}^2_1}{\hat{S}^2_2} \]
Sotto la condizione di campioni indipendenti e \(X\sim N(\mu,\sigma^2)\) (ipotesi nulla), la statistica è il rapporto fra due v.c. \(\chi^2\), ciascuna rapportata ai propri gradi di libertà e pertanto si distribuisce secondo una \(F\) di Fisher, con gradi di libertà corrispondenti a quelli del numeratore e denominatore.
5. Test sull'omogeneità delle varianze /2
Per eseguire il test conviene porre al numeratore sempre la varianza maggiore, in modo da utilizzare sempre la coda di destra della distribuzione.
Attenzione
Normalmente il test statistico mira a falsificare l'ipotesi nulla, quindi a rifiutare \(H_0\); di conseguenza, l'errore da tenere sotto controllo, scegliendo un opportuno livello di significatività \(\alpha\), è l'errore di primo tipo. In questo test, invece, si vuole accettare l'ipotesi nulla e pertanto l'errore più grave è l'errore di II tipo, che come sappiamo non può essere controllato direttamente. Tuttavia, scegliendo valori più grandi di \(\alpha\), l'errore di II tipo, comunque non controllabile, sarà più piccolo. Per questo test è preferibile indicare un valore di \(\alpha\) pari a \(0,1\).
Accettando l'ipotesi nulla, si assume vera la condizione \(\color{brown}{\sigma^2_1 = \sigma^2_2}\) con probabilità \(1-\alpha\).
Nel caso di tre o più gruppi per verificare se \(\sigma^2_1 = \sigma^2_2 = \cdots = \sigma^2_k\) il test verrà costruito ponendo a rapporto \(\frac{\max{\hat{s}^2}}{{\min{\hat{s}^2}}}\).