Unit 1 - Associazione fra caratteri: definizioni e misure per i caratteri statistici
| Sito: | Federica Web Learning - LMS |
| Corso: | Statistica Psicometrica |
| Unit: | Unit 1 - Associazione fra caratteri: definizioni e misure per i caratteri statistici |
| Stampato da: | Utente ospite |
| Data: | martedì, 3 marzo 2026, 09:19 |
Indice Unit
- 1. L’associazione dei caratteri statistici
- 2. Associazione, Connessione e Correlazione
- 3. Connessione /1
- 4. Connessione /2
- 5. Connessione: perfetta dipendenza /1
- 6. Connessione: perfetta dipendenza /2
- 7. Connessione: indipendenza assoluta /1
- 8. Connessione: indipendenza assoluta /2
- 9. Connessione: indipendenza assoluta /3
- 10. Connessione: misurare il grado di dipendenza /1
- 11. Connessione: misurare il grado di dipendenza /2
- 12. Connessione: misurare il grado di dipendenza /3
- 13. Connessione: misurare il grado di dipendenza /4
- 14. Connessione: misurare il grado di dipendenza /5
- 15. Altre definizioni dell’indice di contingenza \(\chi^2\)
- 16. Gli indici normalizzati di Cramér
- 17. Test del \(\chi^2\) dell’indipendenza fra caratteri nominali /1
- 18. Test del \(\chi^2\) dell’indipendenza fra caratteri nominali /2
- 19. Correlazione
- 20. Codevianza - Covarianza - Correlazione
- 21. Serie correlate e indipendenti /1
- 22. Serie correlate e indipendenti /2
- 23. Serie correlate e indipendenti /3
- 24. Serie correlate e indipendenti /4
- 25. Dimostrazione del massimo della covarianza /1
- 26. Dimostrazione del massimo della covarianza /2
- 27. Verifica di ipotesi del coefficiente di correlazione
- 28. Correlazione per caratteri qualitativi /1
- 29. Correlazione per caratteri qualitativi /2
- 30. Correlazione per caratteri qualitativi /3
- 31. Correlazione per caratteri qualitativi /4
- 32. Correlazione per caratteri qualitativi /5
- 33. Correlazione per caratteri qualitativi /6
- 34. Analisi della dipendenza /1
- 35. Analisi della dipendenza /2
- 36. Analisi della dipendenza /3
- 37. Analisi della dipendenza /4
- 38. Analisi della dipendenza /5
- 39. Analisi della dipendenza /6
- 40. Analisi della dipendenza: Esempio
- 41. Correlazione punto bi-seriale
1. L’associazione dei caratteri statistici
- Quando su ciascuna unità statistica si rilevano due o più caratteri (quantitativi e/o qualitativi) è possibile valutare relazioni di dipendenza del tipo causa/effetto o relazioni di interdipendenza utili ai fini di studiare e prevedere in che misura un carattere possa influenzare l’altro (o gli altri).
- Noi ci occupiamo solo di statistica bivariata (lasciando da parte la multivariata)
- Come possiamo definire la condizione di massima in/dipendenza?
- la dipendenza massima fra due caratteri si determina se per ciascuna unità statistica la conoscenza della modalità di un carattere implica la conoscenza della modalità anche dell’altro carattere
- la massima indipendenza implica che la conoscenza della distribuzione congiunta dei due caratteri non migliora la nostra conoscenza rispetto alla informazione delle distribuzioni marginali
2. Associazione, Connessione e Correlazione
Nello studio della dipendenza fra caratteri, si tende a fare confusione tra Associazione, Connessione, Correlazione e Dipendenza.
- Se fra due caratteri la dipendenza è massima, la conoscenza di uno completa anche la conoscenza dell’altro, in questo caso si parlerà di dipendenza perfetta. Viceversa, se la conoscenza di uno non migliora la nostra conoscenza dell’altro, allora diremo che tra i due caratteri c’è una condizione di indipendenza assoluta.
- Notare che è stato utilizzato l’aggettivo perfetta per riferirsi alla massima condizione di dipendenza, mentre è stato utilizzato l’aggettivo assoluta quando si parla di indipendenza. Più avanti sarà possibile chiarire la differenza.
Associazione
Lo studio dell’associazione valuta in che misura la condizione tra due caratteri si discosta dalla condizione di indipendenza assoluta. In alcune condizioni sarà possibile anche determinare in che misura ci si avvicina alla condizione di dipendenza perfetta, mentre in altri no.
3. Connessione /1
Siano \(X\) e \(Y\) due caratteri qualitativi, si definisce connessione lo studio delle relazioni fra caratteri qualitativi (o categorici).
Consideriamo che il carattere \(X\) può assumere le modalità \(X_1;X_2;X_3\) e che al carattere \(Y\) si associano le modalità \(Y_1; Y_2; Y_3\).
- Distribuzione delle frequenze congiunte.

- Indichiamo con \(\color{brown}{i}\) e \(\color{brown}{j}\) la generica riga e la generica colonna e con \(I\) il totale delle righe e \(J\) il totale delle colonne.
Nell’esempio: \(I = J = 3\).
- Definizioni:
\(n_{ij}\) frequenza congiunta: conteggio delle unità statistiche che presentano congiuntamente le modalità \(X_i\) e \(Y_j\);
\(n_{i\cdot}\) e \(n_{\cdot j}\) frequenze marginali riga e colonna:
\(n_{i\cdot} = \sum_{\color{brown}{j}=1}^{J}{n_{i\color{brown}{j}}}\)
\(n_{\cdot j} = \sum_{\color{brown}{i}=1}^{I}{n_{\color{brown}{i} j }}\)
\(n_{\cdot \cdot}\) somma totale per riga e per colonna.
4. Connessione /2
- Distribuzione delle frequenze relative congiunte.
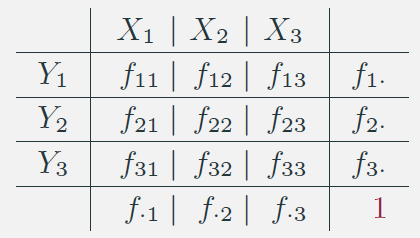
- Indichiamo con \(\color{brown}{i}\) e \(\color{brown}{j}\) la generica riga e la generica colonna e con \(I\) il totale delle righe e \(J\) il totale delle colonne.
Nell’esempio: \(I = J = 3\).
- Definizioni:
\(f_{ij}\) frequenza relativa congiunta: conteggio delle unità statistiche che presentano congiuntamente le modalità \(X_i\) e \(Y_j\);
\(f_{i\cdot}\) e \(f_{\cdot j}\) frequenze relative marginali riga e colonna:
\(f_{i\cdot} = \sum_{\color{brown}{j}=1}^{J}{f_{i\color{brown}{j}}}\)
\(f_{\cdot j} = \sum_{\color{brown}{i}=1}^{I}{f_{\color{brown}{i} j }}\)
\(f_{\cdot \cdot}f_{\cdot \cdot}\) ovviamente!
5. Connessione: perfetta dipendenza /1
La perfetta dipendenza presuppone che ad ogni modalità di un carattere corrisponda una sola modalità dell’altro per cui conoscendone uno si conosce anche l’altro.
- Esempio di perfetta dipendenza:
\(X\) indica il genere letterario e \(Y\) il genere cinematografico preferiti.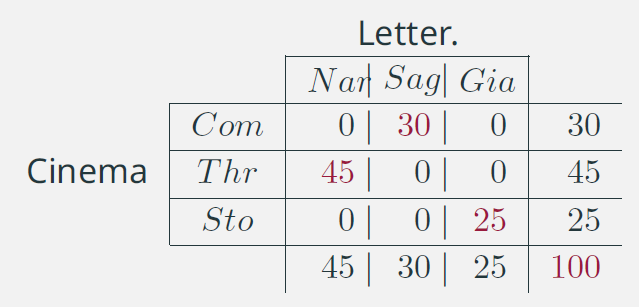
- Se una persona gradisce come genere letterario la Narrativa (Nar), sappiamo che come genere cinematografico gradisce il Thriller (Thr)
- (Analogamente) Se una persona gradisce come genere cinematografico la Commedia (Com), sappiamo che come genere letterario gradisce la Saggistica (Sag)
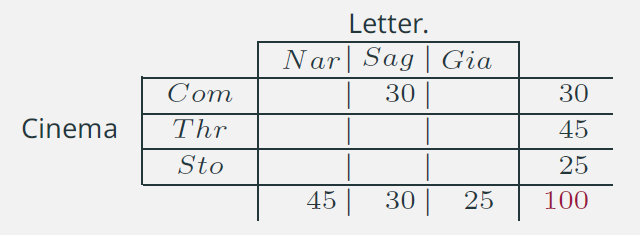
- Queste valutazioni che riguardano la dipendenza non tengono conto di alcun nesso di causalità: i due caratteri sono presi in considerazione in maniera del tutto simmetrica.
6. Connessione: perfetta dipendenza /2
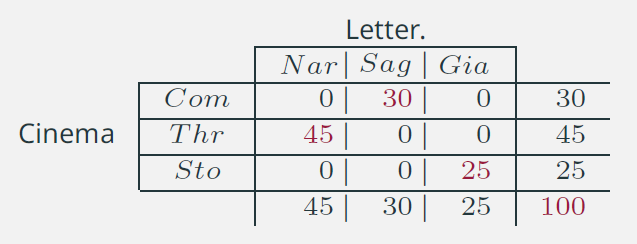
- E’ evidente che la condizione di perfetta dipendenza:
- presuppone che le modalità delle due variabili siano di eguale numero (in questo esempio 3 e 3);
- implica che le distribuzioni marginali abbiano gli stessi valori (anche se in ordine diverso);
- non è unica: altre configurazioni sono possibili.
7. Connessione: indipendenza assoluta /1
L’indipendenza assoluta implica che la conoscenza della distribuzione congiunta non migliora la nostra conoscenza rispetto alla informazione delle distribuzioni marginali.
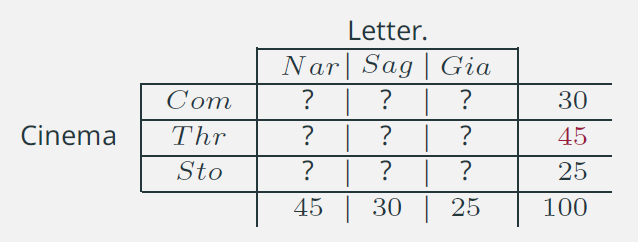
Riprendiamo lo stesso esempio e assumiamo di conoscere solo le marginali (il marginale di riga, per esempio).
Se dovessimo attribuire ad una delle tre modalità (Com, Thr o Sto) una generica unità statistica conoscendo solo la marginale la scelta dovrà necessariamente ricadere su Thr. In questo modo, infatti, siamo certi di minimizzare l’errore dovuto ad errate attribuzioni: nel 45% dei casi l’attribuzione sarà corretta e nel 55% avremo effettuato una attribuzione errata. Questa soluzione, evidentemente, resta preferibile rispetto alle altre due opzioni: Com 70% di errori e Sto 75%.
8. Connessione: indipendenza assoluta /2
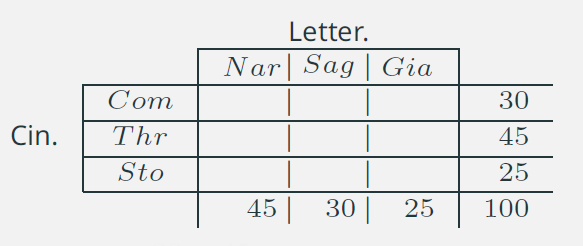
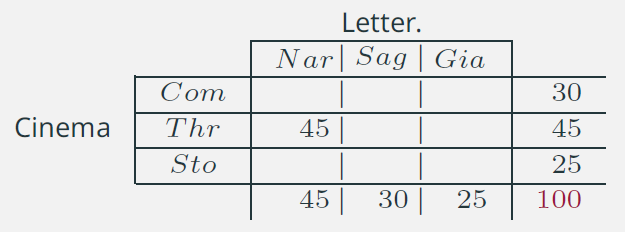
Come dovrebbe presentarsi la distribuzione congiunta perché sia verificata la condizione di indipendenza?
Ciascuna riga/colonna deve essere proporzionale al suo marginale corrispondente, in questo modo l’informazione della distribuzione marginale verrebbe ad essere replicata proporzionalmente per righe e per colonne.
La proporzione:
\[ \color{brown}{ \hat{n}_{ij} : n_{i\cdot} = n_{\cdot j} : n_{\cdot \cdot} } \]
ci permetterà di determinare la frequenza teorica \(\hat{n}_{ij}\) sotto l’ipotesi di indipendenza.
9. Connessione: indipendenza assoluta /3
- \(\displaystyle{\hat{n}_{11} = \frac{30\times 45}{100} =13,5} \)
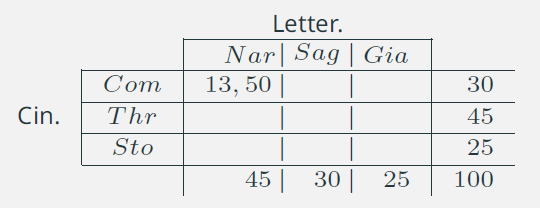
- \(\displaystyle{\hat{n}_{12} = \frac{30\times 30}{100} =9}\)
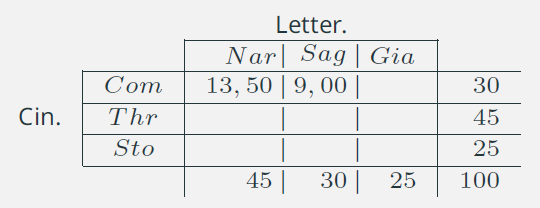
- \(\displaystyle{\hat{n}_{13} = 30 - 13,5 - 9 = 7,5}\)
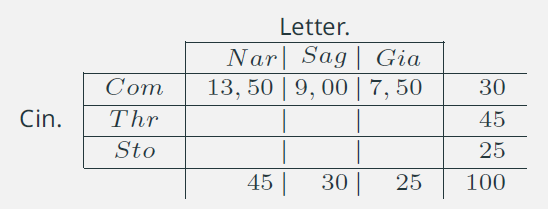
- \(\dots\)
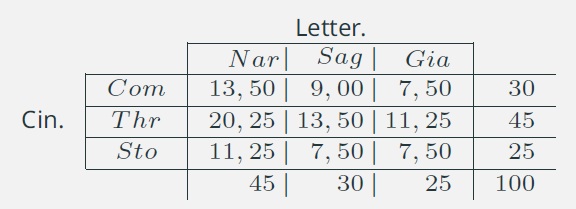
Notare che i marginali restano invariati!
10. Connessione: misurare il grado di dipendenza /1
Abbiamo definito le condizioni estreme: dipendenza perfetta e indipendenza assoluta, come possiamo valutare il grado di associazione di una tabella date le distribuzioni marginali?
Consideriamo lo stesso esempio, a sinistra abbiamo una tabella che non corrisponde a nessuna delle due condizioni estreme. A destra abbiamo la tabella determinata sotto la condizione di indipendenza, che avevamo già calcolato e che non varia finché le marginali restano le stesse.
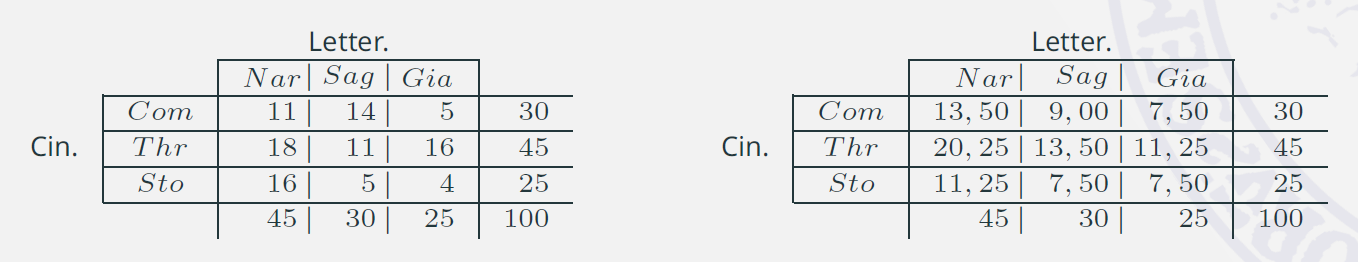
11. Connessione: misurare il grado di dipendenza /2
L’indice di accostamento \(\chi^2\)

Bisogna confrontare le frequenze osservate con le frequenze teoriche (o dette anche attese) e stabilirne il grado di accostamento
- Considerando che i marginali restano invariati, un confronto semplice produrrebbe come risultato \(0\)
- La quantità \((n_{ij}-\hat{n}_{ij})\) viene definita contingenza
\[ \sum_{i}^{I}{\sum_{j}^{J}{\left(n_{ij} - \hat{n}_{ij}\right) }} = \color{brown}{0} \] - Elevando al quadrato le contingenze si evita la compensazione
\[ \sum_{i}^{I}{\sum_{j}^{J}{\left( n_{ij} - \hat{n}_{ij} \right)^{\color{brown}{2}}}} \] - Ponderando per l’inverso delle frequenze teoriche si attribuisce un peso maggiore alle contingenze che hanno frequenze teoriche più basse.
\[ \color{brown}{\chi^2} = \sum_{i}^{I}{ \sum_{j}^{J}{\frac{\left(n_{ij} - \hat{n}_{ij}\right)^2}{\hat{n}_{ij}}}} \]
12. Connessione: misurare il grado di dipendenza /3
L'indice di contingenza quadratica media \(\chi^2\)
\[\color{brown}{\chi^2} = \sum_{i}^{I}{ \sum_{j}^{J}{\frac{\left(n_{ij} - \hat{n}_{ij}\right)^2}{\hat{n}_{ij}}}} \]
- L'indice \(\chi^2\) può assumere solo valori \(\geq 0\) e risente della numerosità totale
- L'indice \(\phi^2 = \chi^2\frac{1}{n_{\cdot \cdot} }\) varia fra \(0\) e \(\min{\left\{(I-1); (J-1)\right\}}\)
- L'indice \(C\) di Cramér è un indice normalizzato di associazione
\[ 0 \leq C = \frac{\phi^2}{\min{\left\{(I-1); (J-1)\right\}}} \leq 1 \]
- L'indice \(V\) di Cramér si ricava facendo la radice quadrata dell'indice \(C\) e ne rappresenta la sua versione linearizzata
\[ 0 \leq V = \sqrt{\frac{\phi^2}{\min{\left\{(I-1); (J-1)\right\}}}} \leq 1 \]
13. Connessione: misurare il grado di dipendenza /4
Misure di associazione basate sulla
Riduzione dell’Errore di Previsione
L’indice \(\color{brown}{\chi^2}\) e gli indici da esso derivati considerano i caratteri in modo simmetrico e sono utili per valutare l’interdipendenza. Esistono, invece, indici specifici
che permettono di assumere l’esistenza di una relazione di dipendenza fra i caratteri o una relazione di antecedenza e conseguenza.
Consideriamo i caratteri Tipo di famiglia (TF: Sin=Singolo, Bam =Fam. con bambini, Rag = Famiglia con figli grandi)
e tipo di auto acquistata (AU: Ber=Berlina, SW=Station Wagon, SUV). La scelta dell’auto dipende dalla tipologia della famiglia e non il viceversa. In generale le righe della tabella riportano le modalità del carattere indipendente (TF), mentre le
colonne sono riservate alle modalità del carattere dipendente.
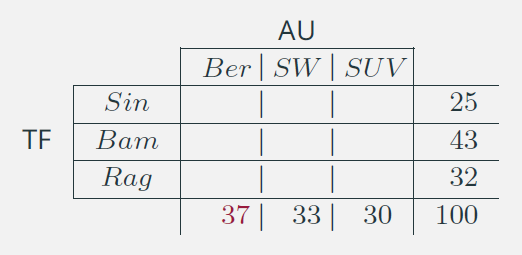 |
Conoscendo solo la marginale (colonna) per ridurre l’errore di previsione consideriamo che la scelta ricada sempre sulla categoria modale (Berlina). In questo modo l’errore commesso è del 63%. |
|---|
14. Connessione: misurare il grado di dipendenza /5
Misure di associazione basate sulla
Riduzione dell’Errore di Previsione
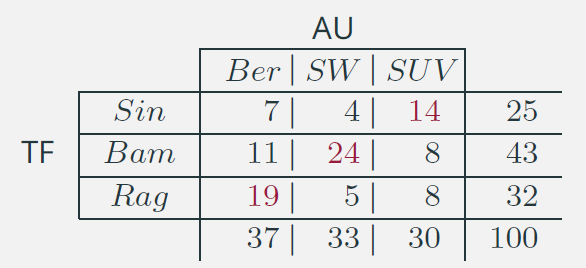
- Tipo di famiglia (TF)
Sin = Single
Bam = Fam. con bambini
Rag = Famiglia con figli grandi
- Tipo di auto acquistata (AU)
Ber = Berlina
SW = Station Wagon
SUV = SUV
Usando lo stesso criterio di attribuzione, basato sulla categoria modale, per ciascuna riga della distribuzione congiunta, la nostra decisione cambierà in funzione della tipologia di famiglia:
- Sin \(\rightarrow\) SUV
- Bam \(\rightarrow\) SW
- Rag \(\rightarrow\) Ber
L’errore di previsione diventerà:
Sin : \(25 - 14 = 11\)
Bam : \(43 - 24 = 19\)
Rag : \(32 - 19 = 13\)
Totale \(= 43\)
\[ 0 \leq \lambda = \frac{63-43}{63} = 0,317 \leq 1 \]
15. Altre definizioni dell’indice di contingenza \(\chi^2\)
L’indice \(\chi^2\) può essere anche visto come una media ponderata del grado di eterogeneità delle righe (o delle colonne) di una tabella di contingenza di \(I\) righe e \(J\) colonne con generico elemento \(n_{ij}\)
\[ \begin{eqnarray}\nonumber H^2 &=& \sum_{j=1}^{J}{n_{\cdot j}\sum_{i=1}^{I}{\frac{(n_{ij}/n_{\cdot j} - n_{i\cdot})^2}{n_{i\cdot}}} } =\cr &=& \sum_{j=1}^{J}n_{\cdot j}{\sum_{i=1}^{I}{\frac{1}{n_{i\cdot}}\left(\frac{n_{ij}}{n_{\cdot j}} - n_{i\cdot}\right)^2 }} = \sum_{j=1}^{J}n_{\cdot j}{\sum_{i=1}^{I}{\frac{1}{n_{i\cdot}}\left(\frac{n_{ij}^{2}}{n_{\cdot j}^{2}} - 2\frac{n_{ij}n_{i\cdot} }{n_{\cdot j}} + n_{i\cdot}^{2}\right) }} =\cr &=& \sum_{j=1}^{J} n_{\cdot j} \sum_{i=1}^{I}\frac{n_{ij}^2}{n_{i\cdot}n_{\cdot j}^2} -2\sum_{j=1}^{J} n_{\cdot j} \sum_{i=1}^{I}\frac{1}{n_{i \cdot}} \frac{n_{ij}n_{i \cdot}}{n_{\cdot j}} +\sum_{j=1}^{J} n_{\cdot j}\sum_{i=1}^{I}\frac{1}{n_{i \cdot}} n_{i\cdot}^2 = \cr &=& \sum_{j=1}^{J}\sum_{i=1}^{I}\frac{n_{ij}^2}{n_{i\cdot}n_{\cdot j}} -2 \sum_{j=1}^{J}\sum_{i=1}^{I}n_{ij} + \sum_{j=1}^{J}\sum_{i=1}^{I}n_{i\cdot}n_{\cdot j} = \cr &=& \color{brown}{\boxed{\sum_{j=1}^{J}\sum_{i=1}^{I}\frac{n_{ij}^2}{n_{i\cdot}n_{\cdot j}} - n_{\cdot\cdot} } } \end{eqnarray} \]
E' facile verificare la seguente uguaglianza
\[ \sum_{j=1}^{J}\sum_{i=1}^{I}\frac{n_{ij}^2}{n_{i\cdot}n_{\cdot j}} -n_{\cdot\cdot} = \sum_{j=1}^{J}\sum_{i=1}^{I}\frac{(n_{ij} - n_{i\cdot}n_{\cdot j})^2}{n_{i\cdot}n_{\cdot j}} = \chi^2 \]
16. Gli indici normalizzati di Cramér
Ripartiamo dalla seguente espressione
\[ \chi^2 = \sum_{i=1}^{I}\sum_{j=1}^{J}\frac{n_{ij}^2}{n_{i\cdot}n_{\cdot j}} - n_{\cdot\cdot} \]
ricordando che
\[ \phi^2 = \frac{1}{n_{\cdot\cdot}}\chi^2 = \sum_{i=1}^{I}\sum_{j=1}^{J}\frac{f_{ij}^2}{f_{i\cdot}f_{\cdot j}} -1 \]
assumiamo che \(I > J\) (il numero di righe è maggiore del numero di colonne) e consideriamo solo la \(i\)-esima riga della tabella
\[ \phi^2_{(i)} = \sum_{j=1}^{J}\frac{f_{ij}^2}{f_{i\cdot}f_{\cdot j}} = \sum_{j=1}^{J}\frac{f_{ij}}{f_{i\cdot}}\frac{f_{ij}}{f_{\cdot j}} \]
osservando che \(\sum_{j=1}^{J}f_{ij}/ f_{i \cdot} = 1\) si deduce che \(\phi^2_{(i)}\) è una media ponderata delle quantità \(f_{ij}/ f_{\cdot j}\). Essendo una media gode della proprietà della internalità e raggiunge il suo massimo \(1\) quando sulla riga esiste un solo valore \(f_{ij}\) diverso da zero sotto la condizione per cui \(f_{\cdot j} > 0\) \(\forall j \in\{1,\ldots J\}\) (non ci devono essere modalità con frequenza marginale uguale a \(0\)). Se \(\phi^2_{(i)}\) raggiunge il massimo per tutte le righe, l'indice \(\phi^2\) avrà raggiunto il suo massimo in \(I-1\).
17. Test del \(\chi^2\) dell’indipendenza fra caratteri nominali /1
- In un contesto inferenziale, in cui il totale della tabella \(n_{\cdot \cdot}\) rappresenta l’ampiezza del campione e la frequenza di ciascuna cella \(n_{ij}\) è la determinazione di una variabile casuale multinomiale, allora \(\chi^2\) è anche una statistica campionaria.
- Si dimostra che la distribuzione della statistica campionaria \(\chi^2\) approssima la distribuzione della v.c. \(\chi^2\) con gradi di libertà pari al numero delle righe meno per il numero delle colonne meno uno: g.l. = \((r - 1) \times (c - 1)\).
- Esiste una statistica, una statistica campionaria \(\chi^2\) ed una distribuzione \(\chi^2\). Poiché si tratta di entità differenti che hanno lo stessa denominazione, per motivi che adesso appaiono più che ovvi, bisogna fare molta attenzione a non fare confusione.
- La bontà dell’approssimazione è condizionata dalla frequenza di ciascuna cella. Per garantire una approssimazione soddisfacente si richiede che la frequenza osservata di ciascuna cella sia almeno pari \(5\). Questa regola è dettata dall’esperienza e dal buon senso. La numerosità di una singola cella è solo uno degli elementi che condizionano la bontà dell’adattamento.
18. Test del \(\chi^2\) dell’indipendenza fra caratteri nominali /2
Definizione del test
- Il test dell'associazione del \(\chi^2\) si articola sulle seguenti ipotesi:
\(H_0: \chi^2_{gl} = 0\)
\(H_1: \chi^2_{gl} > 0\) - Osservare che questo test è valido solo \(H_0: \chi^2_{gl} = 0\) (per capirci non è possibile eseguire questo test per \(\chi^2_{gl} = 2\) o comunque per qualsiasi altro valore che non sia \(0\)) perché la statistica campionaria \(\chi^2_{gl}\) segue l'omonima distribuzione solo sotto \(H_0: \chi^2_{gl} =0\).
- Questo test è un test non parametrico. Infatti, la statistica \(\chi^2\) approssima una distribuzione nota, ma non si riferisce ad alcun parametro.
19. Correlazione
Siano \(X: x_1, x_2, \ldots, x_n\) e \(Y : y_1, y_2, \ldots, y_n\) due variabili rilevate su un collettivo di \(N\) soggetti, diremo che le due variabili sono indipendenti se la conoscenza dell'una non migliora la conoscenza dell'altra variabile. Se la
conoscenza di una permette di determinare il valore dell'altra, allora diremo che le due variabili sono dipendenti.
Nel caso di variabili continue il grado di dipendenza si misura attraverso il coefficiente di correlazione lineare semplice di Bravais-Pearson, che viene indicato generalmente con \(\rho\) (o con \(r\)).
20. Codevianza - Covarianza - Correlazione
Correlazione
Siano \(X = \{x_1, x_2, \ldots, x_N \}\) e \(Y = \{y_1, y_2, \ldots y_N \}\) due variabili osservate su un collettivo di \(N\) unità e aventi media rispettivamente \(\bar{x}\) e \(\bar{y}\)
- si definisce codevianza la quantità
\[codev(X,Y) = \sum_{i=1}^N{(x_i - \bar{x})(y_i - \bar{y}}) \]
- dividendo la codevianza per la numerosità \(N\) si ottiene la covarianza
\[ COV(X,Y) = \frac{1}{N}\sum_{i=1}^N{(x_i - \bar{x})(y_i - \bar{y}}) \]
- dividendo la covarianza per la radice quadrata del prodotto delle deviazioni standard si ottiene il coefficiente di correlazione \(\rho\) compreso fra \(-1\) e \(1\)
\[ -1 \leq \rho(X,Y) = \frac{\frac{1}{N}\sum_{i=1}^N{(x_i - \bar{x})(y_i - \bar{y}})}{\sqrt{\sigma_X^2 \sigma_Y^2}} \leq 1 \]
21. Serie correlate e indipendenti /1
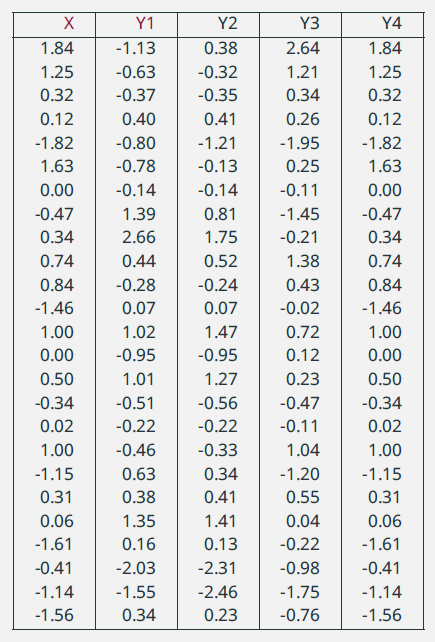 |
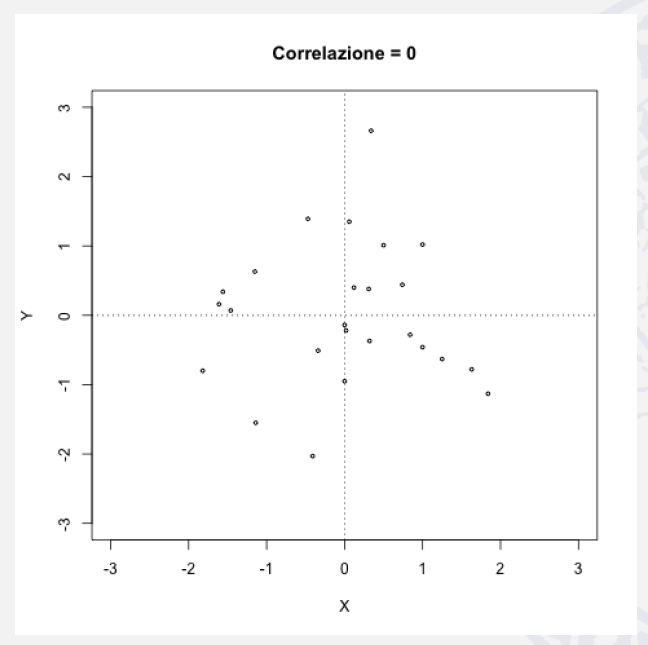 \(\rho = 0\) |
|---|
22. Serie correlate e indipendenti /2
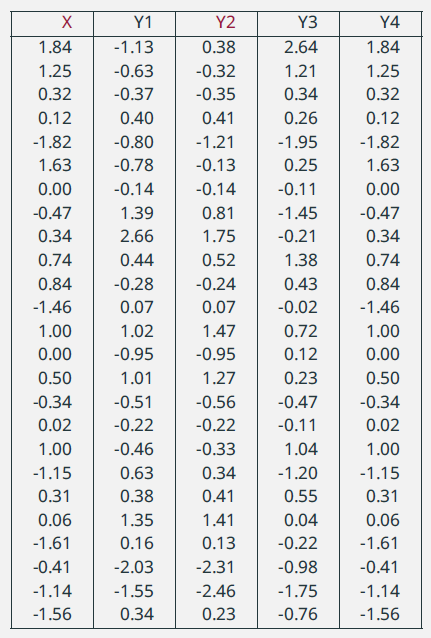 |
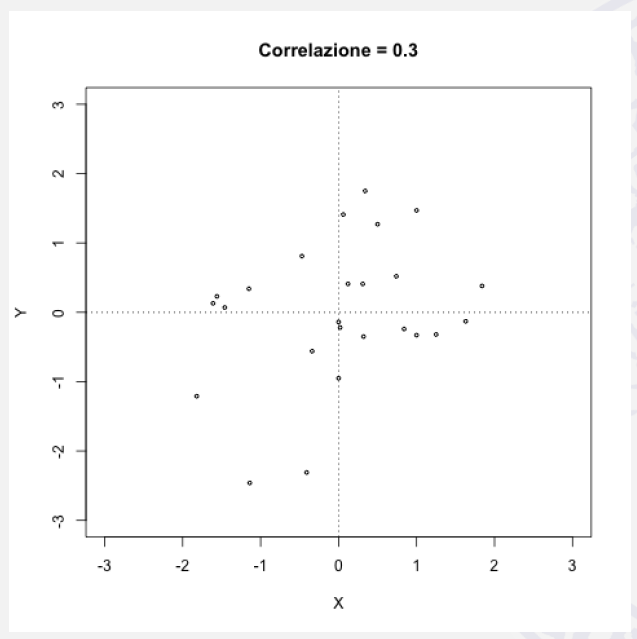 \(\rho=0,3\) |
|---|
23. Serie correlate e indipendenti /3
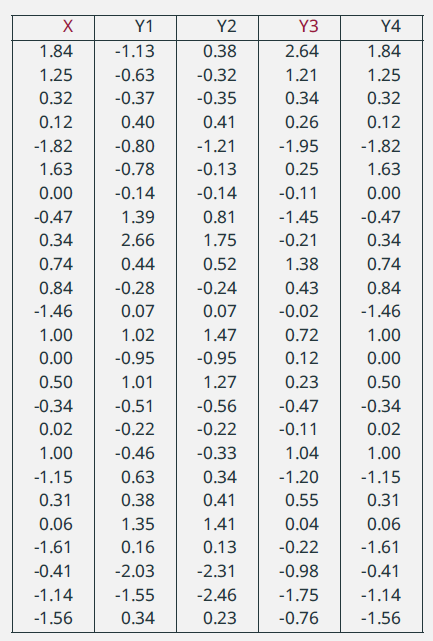 |
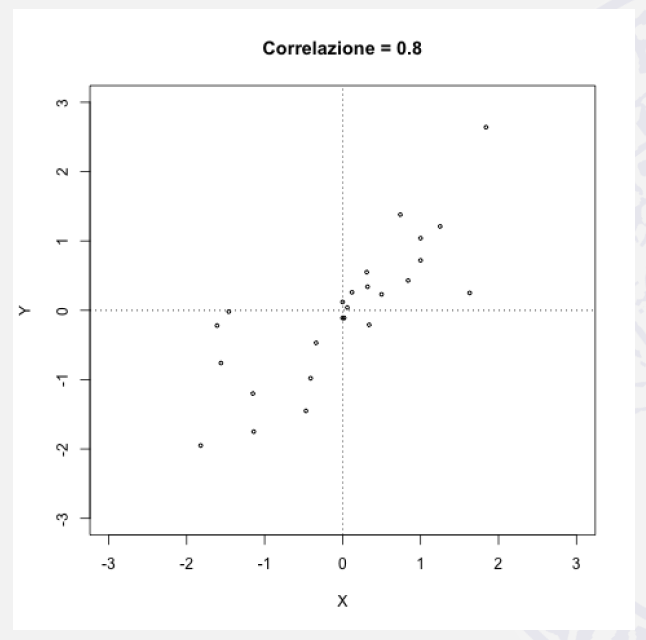 \(\rho = 0,8\) |
|---|
24. Serie correlate e indipendenti /4
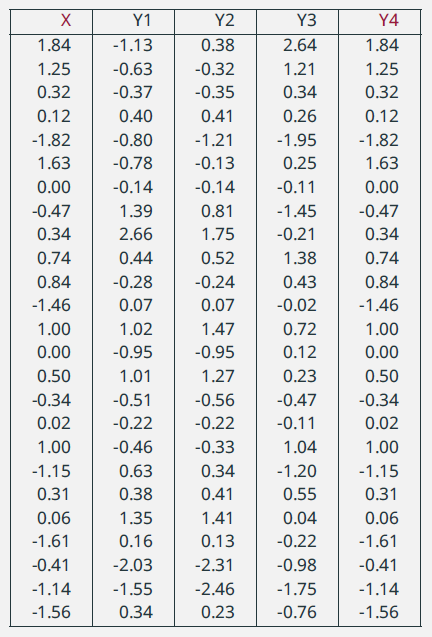 |
|
|---|
25. Dimostrazione del massimo della covarianza /1
Siano \(X\) e \(Y\) due variabili tali che
- \(\bar{x} = \bar{y} = 0\) e
- \(var(X) = \sigma^2_X\) e \(var(Y) = \sigma^2_Y\),
dimostriamo che:
\[ \color{brown}{\boxed{\sum_{i = 1}^{n}{x_i y_i} \leq \sqrt{\sum_{i = 1}^{n}{x^2_i} \sum_{i = 1}^{n}{y^2_i} } } } \]
26. Dimostrazione del massimo della covarianza /2
Dimostrazione
- Consideriamo il polinomio di secondo grado
\[ p = (a_1 + b_1 x)^2 + (a_2 + b_2 x)^2 + \cdots + (a_n + b_n x)^2 \]che non ha radici reali tranne nel caso in cui \(a_1 = a_2 = \cdots = a_n\) e \(b_1 = b_2 = \cdots = b_n\) oppure i coefficienti sono proporzionali fra loro.
- Svolgiamo i quadrati:
\[ a_1^2 + b_1^2x^2 + 2a_1 b_1x + a_2^2 + b_2^2 + 2a_2b_2x + \cdots + a_n^2 + b_n^2x + 2a_nb_nx \]e raggruppiamo\[ x^2\sum_{i=1}^{n}{b_i^2} + 2x\sum_{i = 1}^{n}{a_i b_i} + \sum_{i=1}^{n}{a_i^2} \]ottenendo una equazione di II grado:\[ x^2\underbrace{\sum_{i=1}^{n}{b_i^2}}_{\color{red}{a}} + \Big(\underbrace{2\sum_{i = 1}^{n}{a_i b_i}}_{\color{blue}{b}} \Big)x + \underbrace{\sum_{i=1}^{n}{a_i^2}}_{\color{lime}{c}} = 0 . \]
- Ricordiamo che il discriminante della eq. di II grado è uguale a \(\boxed{\color{blue}{b}^2 - 4\color{red}{a}\color{lime}{c}}\) e l'eq. ammette radici reali e distinte solo se il discriminante \(> 0\).
Il discriminante dell'eq è:
\[\underbrace{4\Big(\sum_{i=1}^{n}{a_i b_i} \Big)^2}_{\color{blue}{b}^2} - 4\underbrace{\sum_{i=1}^{n}{a_i^2}}_{\color{lime}{c}}\underbrace{\sum_{i=1}^{n}{b_i^2}}_{\color{red}{a}}.\]
- Poiché abbiamo scelto i coefficienti \(a\) e \(b\) uguali o proporzionali fra loro, la diseguaglianza \(\sum_{i=1}^{n}{a_i b_i} < \sqrt{\sum_{i=1}^{n}a_i^2\sum_{i=1}^{n} b_i^2}\) è soddisfatta solo se i coefficienti non sono uguali fra loro.
27. Verifica di ipotesi del coefficiente di correlazione
Se i punteggi osservati sono determinazioni di variabili casuali \(X_1\) e \(X_2\), sotto determinate condizioni, è possibile porre a verifica:
\[\color{brown}{H_0: \rho = 0 \hspace{1cm} \text{contro} \hspace{1cm} H_1: \rho \neq 0.}\]
Il test è possibile solo sotto la condizione che \(X_1\) e \(X_2\) siano i.i.d. secondo una distribuzione Normale.
- Per coerenza abbiamo indicato le variabili con \(X_1\) e \(X_2\), invece che con \(X\) e \(Y\) e senza perdere di generalità possiamo assumere che \(\mu_1 = \mu_2 = 0\). Vogliamo utilizzare la statistica campionaria \(r\) come stimatore naturale di \(\rho\).
\[ r = \frac{\mathrm{CODEV}(X_1, X_2)}{\sqrt{\mathrm{DEV}(X_1)\mathrm{DEV}(X_2) }} = \frac{\sum_{i=1}^{n}{X_{i1}X_{i2}}}{\sqrt{\sum_{i=1}^{n}X_{i1}^2\sum_{i=1}^{n}X_{i1}^2}}.\] - La distribuzione della statistica campionaria \(r\) non è nota.
- È tuttavia possibile dimostrare che sotto \(\boldsymbol{H_0: \rho = 0}\) la seguente trasformazione di \(r\) segue una distribuzione \(t\) di Student con \(n-2\) gl:
\[ t_{n-2} = \frac{r\sqrt{n-2}}{\sqrt{1-r^2}}. \]
28. Correlazione per caratteri qualitativi /1
Il concetto di correlazione si può estendere ad altre tipologie di variabili. In particolare esistono misure di correlazione per dati ordinali e per caratteri binari.
Ranghi
- Un indice che trova largo impiego quando si ha a che fare con lo studio della interdipendenza in una coppia di caratteri qualitativi ordinali è il coefficiente di correlazione di \(\rho\) di Spearman (noto anche come indice di cograduazione).
- Il concetto di cograduazione presuppone che sia prima data la definizione di rango.
- Sia \(X= x_1, x_2, \cdots, x_i, \cdots x_n\) una serie per cui \(X\) sia ordinabile, si definisce rango di \(X\) \(R(X)\) la funzione che assegna a ciascuna unità la posizione che occupa nelle serie ordinata in ordine crescente.
- Esempio: siano \(0,5\), \(1,0\), \(1,1\), \(15,0\), \(100,0\) i valori osservati di \(X\) ordinati dal più piccolo al più grande, si avrà che \(R(0,5)=1\), \(R(15,0) = 4\) e così via. Si evince che, qualunque sia la natura del carattere e la sua variabilità intrinseca, i ranghi corrispondenti saranno sempre i numeri naturali da \(1\) fini ad \(n\).
- Nel caso di valori uguali (ties) verrà assegnato a tutti il corrispondente rango medio.
29. Correlazione per caratteri qualitativi /2
Indice di correlazione di Spearman
L'indice di cograduazione di Spearman è definito attraverso la seguente espressione
\[ \rho = \frac{ \sum_{k=1}^{K}{\left(R(x_k) - \frac{(n+1)}{ 2}\right)}{\left(R(y_k) - \frac{(n+1)}{2}\right)}}{\sqrt{\sum_{k=1}^{K}\left( R(x_k) - \frac{(n+1)}{2} \right)^2 \sum_{k=1}^{K}\left( R(y_k) - \frac{(n+1)}{2} \right)^2}}, \]
che non è altro che il coefficiente di correlazione calcolato sui ranghi.
\[ -1 \leq \rho = \frac{ \sum_{k=1}^{K}{(r_k - \bar{r})(s_k - \bar{s})}}{\sqrt{\sum_{k=1}^{K}(r_k - \bar{r})^2\sum_{k=1}^{K}(s_k - \bar{s})^2}} \leq 1, \]
in una notazione più leggera.
30. Correlazione per caratteri qualitativi /3
Dimostriamo che il coefficiente di cograduazione di Spearman si semplifica nella seguente espressione
\[ \boxed{\color{brown}{\rho = 1- \frac{6\sum_{k=1}^{K}{d_k^2}} {n(n^2 - 1)}}} \]
Dove
- \(d_k = (r_{k} - s_{k})\)
- \(\bar{r} = \bar{s} = \displaystyle{\frac{n+1}{2}}\) in virtù delle proprietà della media aritmetica.
Iniziamo dal denominatore
\[\sum_{k=1}^{K}(r_k - \bar{r})^2\sum_{k=1}^{K}(s_k - \bar{s})^2\]
31. Correlazione per caratteri qualitativi /4
Denominatore
Ricordiamo che:\[ \color{brown}{ \boxed{\sum_{k=1}^{n}(r_k - \bar{r})^2 = \sum_{k=1}^{n}(s_k - \bar{s})^2 = \sum_{k=1}^{n}{r_k^2} - \frac{n(n+1)^2}{4} } } \]
e che:
\[ \color{brown}{ \boxed{\sum_{k=1}^{n}{r_k^2} = \frac{n(n+1)(2n+1)}{6} } } \]
è una somma telescopica.
\[ \begin{eqnarray}\nonumber \sum_{k=1}^{n}(r_k - \bar{r})^2 &=& \frac{n(n+1)(2n+1)}{6} - \frac{n(n+1)^2}{4} \\ &=& n(n+1) \frac{n-1}{12} \\[8pt] &=& \frac{n(n^2-1)}{12} \end{eqnarray} \]
32. Correlazione per caratteri qualitativi /5
Somma telescopica
| \[\begin{eqnarray}\nonumber 3\sum_{k=1}^{n}k^2 &=& \sum_{k=1}^{n}(k + 1)^3 - \sum_{k=1}^{n}k^3 - 3\sum_{k=1}^{n}k - n \cr 3\sum_{k=1}^{n}k^2 &=& (n+1)(n+1)^2 - 1 -\frac{3}{2}n(n+1) - n \cr &=& (n+1)\left[(n+1)^2
-\frac{3}{2}n -1\right]\cr &=& \cdots \cr &=& \frac{1}{2}n(n+1)(2n+1) \end{eqnarray}\] Infine abbiamo: \[ \color{brown}{\begin{eqnarray}\nonumber \boxed{\sum_{k=1}^{n}k^2 = \frac{1}{6}n(n+1)(2n+1)} \end{eqnarray}} \] |
\[ \qquad \] |
Digressioni Sviluppiamo \( \sum_{k=1}^{n} r_k^2 \) osservando che \[ (k + 1)^3 - k^3 = 3k^2 + 3k + 1 \] \[\sum_{k=1}^{n}(k+1)^3 - k^3 = (n+1)^3 - 1 \] Somma telescopica \[ \begin{eqnarray}\nonumber 1^3 &=& 1^3\cr 2^3 &=& (1 +1)^3 = 1^3 + 3 + 3 + 1^3 = 8\cr 3^3 &=& (2+1)^3 = 2^3 +3\cdot 2^2 + 3\cdot 2 + 1^3 \cr &=& 8+12 + 6 + 1 = 27\cr &\cdots&\cr (k+1)^3 &=& k^3+3k^2 + 3k +1 \end{eqnarray} \] da cui: \[ 3k^2 = (k+1)^3 - 3k - 1 \] |
|---|
33. Correlazione per caratteri qualitativi /6
Numeratore
| \[\begin{eqnarray}\nonumber & & \sum_{k=1}^{n}{r_k\,s_k} - n\left( \frac{n+1}{2} \right)^2\cr &=& \sum_{k=1}^{n}{r_k\,s_k} - 3n\left( \frac{n+1}{12} \right)(n+1)\cr &=& \sum_{k=1}^{n}{r_k\,s_k} + n\left( \frac{n+1}{12} \right)(-3n - 3)\cr &=& \sum_{k=1}^{n}{r_k\,s_k} + n\left( \frac{n+1}{12} \right)[(n-1) - (4n + 2)]\cr &=& \frac{n(n+1)(n-1)}{12} - \frac{(n+1)(2n + 1)}{6} + \sum_{k=1}^{n}{r_k\,s_k}\cr &=& \frac{n(n^2 - 1)}{12} - \frac{1}{2}\sum_{k=1}^{n}(r_k^2 + s_k^2) + \sum_{k=1}^{n}{r_k\,s_k} \cr & \, & \color{brown}{ \boxed{ = \frac{n(n^2 - 1)}{12} - \frac{1}{2}\sum_{k=1}^{n}(r_k - s_k)^2 } } \end{eqnarray} \] | \[ \qquad \] |
Digressioni \[\bar{r} = \bar{s} = \displaystyle{\frac{n+1}{2}}\]\[\sum_{k=1}^{n} r_k = \sum_{k=1}^{n} s_k = \displaystyle{\frac{n(n+1)}{2}}\] |
|---|
34. Analisi della dipendenza /1
Studio della dipendenza di un variabile continua rispetto ad una variabile nominale
- Ci occupiamo adesso dello studio della dipendenza fra due caratteri. In particolare consideriamo il caso in cui una variabile \(Y\) dipende da una mutabile \(X\).
- In statistica (generalmente) si usa indicare le variabili dipendenti con la \(Y\) e le variabili indipendenti con la \(X\).
- La situazione in cui una variabile dipende da una mutabile è molto frequente nell’analisi dei dati statistici. Meno frequente e più difficile anche da immaginare è il caso in cui una mutabile dipende da una variabile.
- Esempi: reddito \(\Leftarrow\) tipo di laurea, raccolto \(\Leftarrow\) tipo di concime oppure rend. scolastico \(\Leftarrow\) tipo di rinforzo
....
35. Analisi della dipendenza /2
Sia \(Y\) una generica variabile che è stata osservata su un collettivo di \(N = 600\) unità statistiche. La figura rappresenta il boxplot della variabile.
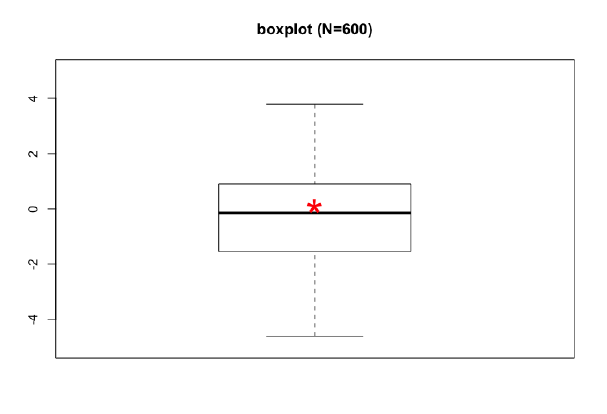
36. Analisi della dipendenza /3
Consideriamo adesso lo stesso esempio, ma assumiamo che oltre ad aver rilevato il carattere \(Y\) abbiamo registrato, sulle stesse unità statistiche, anche un carattere nominale \(X\) che presenta \(3\) modalità.
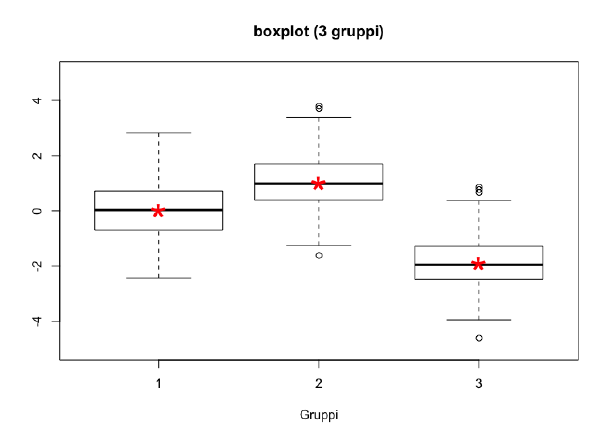
È evidente che la conoscenza di \(X\) migliora la capacità di predire il valore di \(Y\). Possiamo dunque affermare che vi dipendenza fra la variabile \(Y\) e la variabile nominale \(X\).
In che modo possiamo misurare il grado di associazione fra \(Y\) e \(X\)?
37. Analisi della dipendenza /4
Consideriamo le situazioni estreme di assoluta indipendenza e dipendenza perfetta, in corrispondenza delle quali l’indice che si prende in considerazione deve assumere rispettivamente valore \(0\) e il suo massimo.
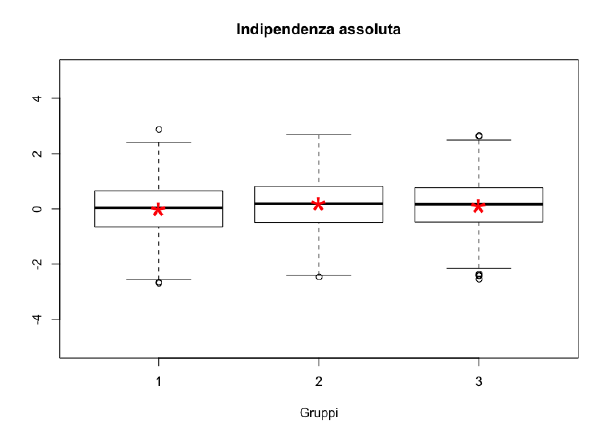
La conoscenza della \(X\) non aggiunge nulla rispetto alla conoscenza della sola variabile \(Y\).
38. Analisi della dipendenza /5
Consideriamo le situazioni estreme di assoluta indipendenza e dipendenza perfetta, in corrispondenza delle quali l’indice che si prende in considerazione deve assumere rispettivamente valore \(0\) e il suo massimo.
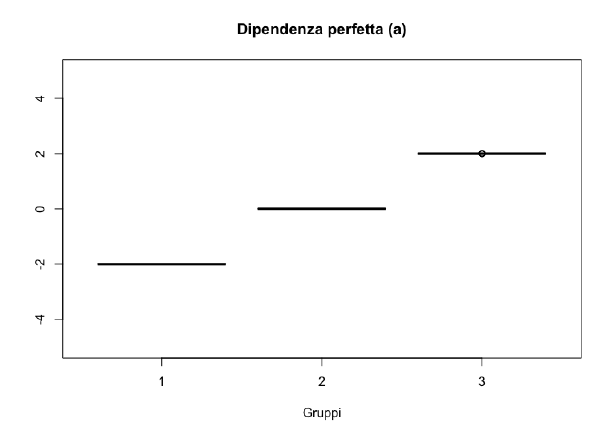
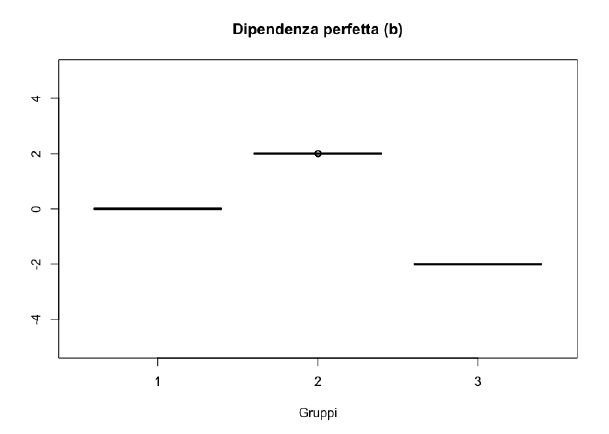
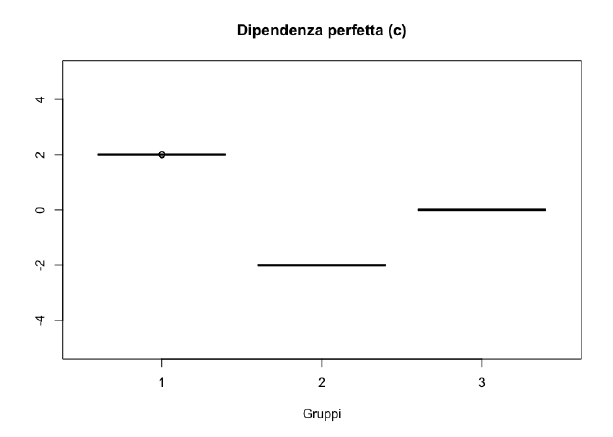
La conoscenza della \(X\) determina automaticamente anche la conoscenza della \(Y\).
39. Analisi della dipendenza /6
Il rapporto di correlazione \(\eta^2\)
Il Teorema della scomposizione della devianza ci dice che la devianza totale della variabile \(Y\) può essere scomposta in due quantità, la cui somma restituisce nuovamente devianza
totale:
\[ DEV(Y) = DEV_{W}(Y) + DEV_B(Y) \]
dove \(DEV_{W}(Y)\) sta ad indicare la somma delle devianze misurate indipendentemente in ciascuna classe, mentre \(DEV_{B}(Y)\) si riferisce alla devianza delle medie parziali (\(\bar{y}_1, \bar{y}_2, \bar{y}_3\)) rispetto alla media generale \(\bar{y}\).
Sfruttando la scomposizione della devianza definiamo l'indice \(\eta^2\) come il rapporto:
\[ 0 \leq \eta^2 = \frac{DEV_B{(Y)}}{DEV{(Y)}} \leq{1} \]
Si osservi che se la devianza nei gruppi è 0 (distribuzioni degenere) allora \(DEV_B(Y) = DEV(Y)\) e quindi \(\eta^2 = 1\). Viceversa, se \(DEV_B(Y)=0\) allora \(\eta^2=0\).
40. Analisi della dipendenza: Esempio
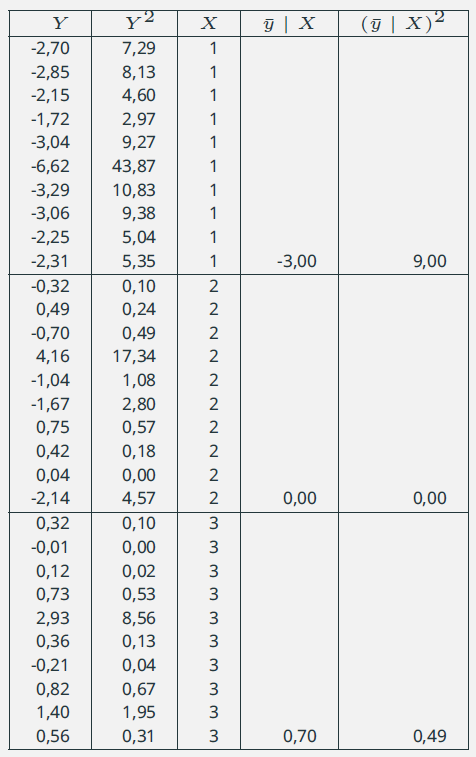 |
Calcolo del coefficiente \(\eta^2\) \({\bar{y}}= \displaystyle{\frac{1}{30}\sum_{i=1}^{30}{y_i} = 0,77}\) \(N{\bar{y}}^2= 30\times 0,587=17,63\) \(\sum{Y^2}=146,41\) \(DEV(Y)= 146,41 - 17,63 = 128,78\) \(DEV_W(Y)=10*((Y\mid X_1)^2 + (Y\mid X_2)^2 +\) \(\qquad \qquad \qquad + (Y\mid X_3)^2) - \sum{Y^2} = 77,27\) \[ \eta^2 = \frac{77,27}{128,78} = 0,6 \]E' possibile linearizzare l'indice usando la radice quadrata \[ \eta = \sqrt{\eta^2} = \sqrt{0,6} = 0,77 \] |
|---|
41. Correlazione punto bi-seriale
Siano \(X\) e \(Y\) due caratteri tali che \(X\) è una variabile dicotomica, ovvero assume solo valori in \(\{0, \, 1\}\) e \(Y\) e una variabile continua definita in \(\mathbb{R}\) o in un suo sottoinsieme il coefficiente di correlazione
\[ \begin{eqnarray}\nonumber \rho_{pb} = \frac{\sum_{i=1}^{n}(x_i -\bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2\sum_{i=1}^{n}(y_i - \bar{y})^2}} \end{eqnarray} \]
è detto coefficiente di correlazione punto-biseriale. Si osserva che \(\rho_{pb}\) ha la stessa formulazione di \(\rho\) e come \(\rho\) varia fra \(-1\) e \(1\).
Tuttavia è interessante osservare che se il numeratore viene riscritto secondo la seguente formulazione \(\sum_{i=1}^{n}x_iy_i - n\bar{x}\bar{y}\), moltiplicando le \(x_i\) per le \(y_i\) si sommeranno solo i valori corrispondenti alle osservazioni che presentano il valore \(1\) nella variabile \(X\) e il prodotto \(n\bar{x}{Y}\) è una frazione della media di \(Y\) proporzionale a \(\sum_{i=1}^{n}x_i/n\). Stesso discorso si può fare per il denominatore: viene presa in considerazione una frazione della varianza proporzionale ai soggetti che presentano valor \(1\) in \(X\).
Ricordando che \((\bar{y}\mid 1 - \bar{y}) = -(\bar{y}\mid 0 - \bar{y})\), il coefficiente \(\rho_{pb}\) risulta essere una misura normalizzata dello scostamento dalla media generale \(\bar{y}\) delle medie condizionate (\(\bar{y}\mid 1\)) o (\(\bar{y}\mid
0\)).