Il fissaidee

Sito:	Federica Web Learning - LMS
Corso:	Scienze fisiche di base
Unit:	Il fissaidee

Stampato da:	Utente ospite
Data:	martedì, 1 luglio 2025, 01:21

Indice Unit

1. La notazione scientifica
2. Le unità di misura fondamentali del sistema internazionale (SI)
3. L'analisi dimensionale
4. Statistica: il minimo essenziale
5. Istogrammi

1. La notazione scientifica

Prima tappa

Le grandezze fisiche possono spesso variare di molti ordini di grandezza. Quindi è comodo esprimerle per mezzo di potenze di dieci, con un esponente uguale al numero di cifre che seguono la prima cifra non nulla.
Ad esempio: anziché scrivere 235000000 scriveremo → 2,35 X 10⁸

PER SEMPLIFICARE: MULTIPLI E SOTTOMULTIPLI

Spesso è comodo utilizzare multipli o sottomultipli dell’unità di misura per una grandezza, dove ogni multiplo è mille volte più grande (ed ogni sottomultiplo mille volte più piccolo) del precedente. Ecco una scala dei più comuni, esemplificati nel caso della potenza (che come vedremo si misura in watt, W).

Ad esempio con la potenza prodotta da ciascun reattore di una tipica centrale nucleare (1GW) potremmo far funzionare un milione di miliardi di orologi al quarzo, ciascuno dei quali consuma circa 1 μW (ma poi a chi li vendiamo?)

Per spostarti tra le pagine del fissaidee utilizza le frecce azzurre.

2. Le unità di misura fondamentali del sistema internazionale (SI)

Il Sistema Internazionale (SI) assume sette unità fondamentali, che possono essere combinate in modo da ottenere le unità di misura di ogni altra grandezza fisica:

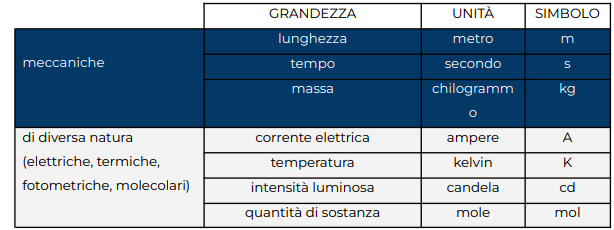
DALLE UNITÀ ALLE DIMENSIONI

Talvolta potrebbe farci comodo utilizzare anche altre unità, più adatte al problema considerato o di uso comune. Ad esempio, è sicuramente più facile misurare la distanza delle stelle in anni-luce piuttosto che in metri, o per un marinaio dare una velocità in nodi, piuttosto che in metri al secondo, o una dieta in calorie piuttosto che in joule.
Unità di misura diverse che si riferiscono alla stessa grandezza fisica hanno però le stesse dimensioni. Così metro e centimetro sono entrambi una lunghezza, o joule e caloria un’energia. Usare le dimensioni, anziché le specifiche unità, elimina ogni possibile confusione.
Le dimensioni di una grandezza fisica si indicano di solito in parentesi quadra, usando questi simboli per le grandezze principali del S.I.

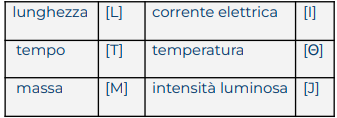
Così ad esempio le dimensioni di una velocità, che è una lunghezza divisa per un tempo,
si indicano con \( [\textbf{V}]=[\textbf{L}]/[\textbf{T}] \) o ancora meglio \( [\textbf{V}]=[\textbf{L}][\textbf{T}]^{-1} \).
N.B. la “quantità di sostanza” è un numero puro, cioè è adimensionale (numero di
moli o di molecole) quindi introdurre un simbolo per essa è poco utile e fuorviante.

Al termine di un problema è estremamente utile fare un check delle dimensioni. Ad esempio, di aver calcolato l’energia di un corpo come \( E = f(x,t) \), dove \( f(x,t) \) è una funzione della posizione \( x \) e del tempo \( t \). Allora, poiché un’energia è dimensionalmente una massa per una velocità al quadrato, è essenziale che anche le dimensioni di \( f(x,t) \) siano \( [f] = [\textbf{M}][\textbf{L}]^{2}[\textbf{T}]^{-2} \). Altrimenti, abbiamo sbagliato di sicuro!

3. L'analisi dimensionale

Spesso si può capire da quali grandezze dipenda una certa quantità fisica Q, nonché su come ciascuna di queste grandezze entri nell’espressione per Q, combinandole nell’unico modo in cui diano le dimensioni corrette per Q.

Un esempio? il periodo di oscillazione τ di un pendolo, che ha le dimensioni di un tempo, dipenderà sicuramente dalla sua lunghezza \( l \), dall’accelerazione di gravità \( g \), ed in linea di principio anche dalla sua massa \( \textbf{m} \). Ma per ottenere un tempo dovremmo in qualche modo “far sparire” la massa, che né le dimensioni \( l \) di né quelle di \( g \) contengono. Quindi il periodo non può dipendere da m. L’unica combinazione possibile delle rimanenti grandezze che dia un tempo è la radice di l su \( g \): \( \left[(l/g)^{1/2}\right]=\textbf{L}^{1/2}x\left[\textbf{LT}^{-2}\right]^{-1/2}=\left[\textbf{T}\right]. \)
Quindi il periodo deve potersi scrivere come \( \tau= C\sqrt{\frac{l}{g}} \) dove \( C \) è una costante adimensionale, ossia un numero puro.

I GRAFICI

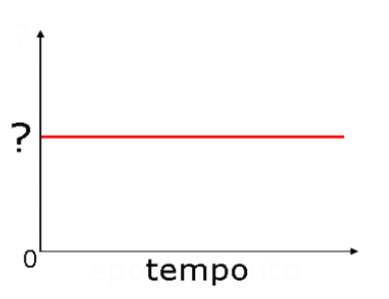
No labels, no physics! Un grafico dove non vengano indicate le grandezze fisiche rappresentate sugli assi non serve assolutamente a nulla! Ad esempio, nel grafico a fianco, che vorrebbe descrivere il moto di un corpo lungo una retta:

se ? = spostamento, il corpo se ne sta fermo
se ? = velocità il corpo si muove di moto rettilineo uniforme
se ? = accelerazione il corpo si muove di moto uniformemente accelerato

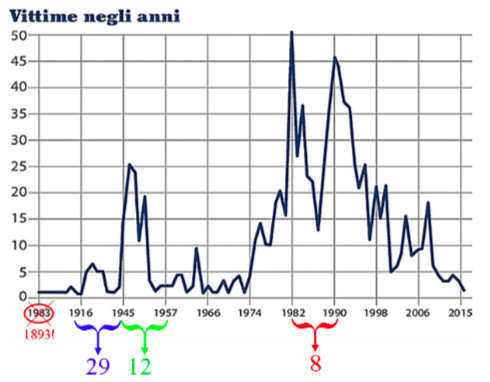
Assi sì, ma fatti bene! Spesso (soprattutto nell’infografica dei giornali) si trovano grafici che lasciano a dir poco perplessi, soprattutto perché gli assi sono disegnati in modo a dir poco “creativo”…guardate ad esempio questo grafico, tratto da uno dei maggiori quotidiani italiani, che vorrebbe rappresentare i decessi provocati nel tempo dalla mafia. A parte il banale refuso per il primo anno, che è ovviamente il 1893, intervalli uguali sull’asse delle ascisse rappresentano spesso un numero di anni molto diverso. Ciò, oltre che sbagliato, è davvero fuorviante!

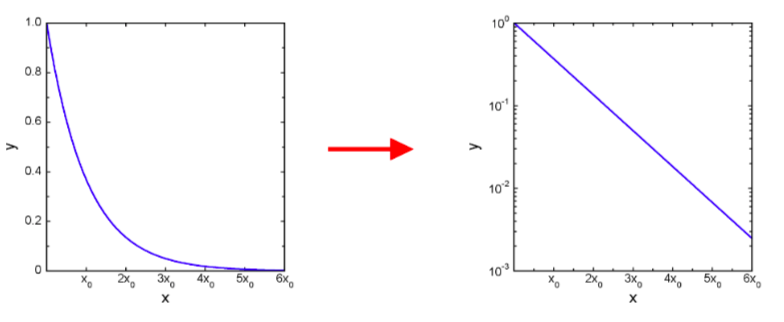
Gli assi logaritmici. Quando una grandezza fisica ha un comportamento particolare, può essere comodo rappresentarla utilizzando, anziché degli assi lineari, assi con una spaziatura logaritmica dell’ascisse, o dell’ordinate, o di entrambe. Ad esempio:

andamento esponenziale: \( y=exp (-x/x_{0} ) \)

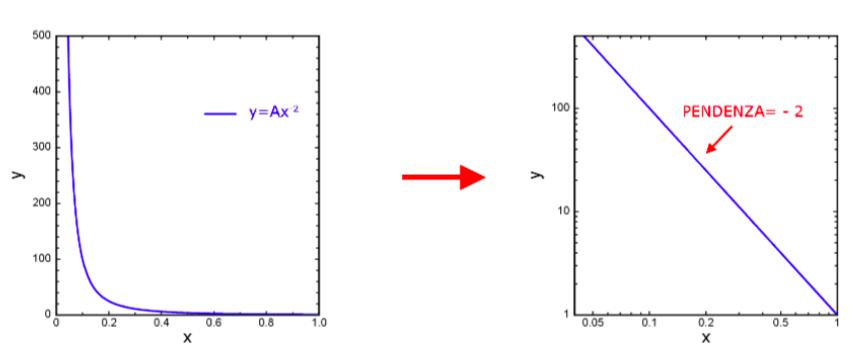
andamento a legge di potenza: \( y=Ax^{c} \)

4. Statistica: il minimo essenziale

Distribuzioni di una grandezza statistica. Molte grandezze non hanno UN valore ben determinato, ma piuttosto possono assumere una serie di valori diversi entro un certo intervallo. Indichiamo con \( \textbf{K} \) una grandezza di questo tipo e con\( k \) un generico valore tra quelli che essa può assumere (che possono essere anche infiniti!). Se ora raccogliamo un campione statistico costituito da \( N \) risultati di una misura della variabile ed indichiamo con \( n_{k} \) il numero di volte che si ottiene il valore \( k \), possiamo definire le frequenze relative \( f_{k}=\frac{n_{k}}{N} \) Un grafico delle \( f_{k} \) verso \( k \) viene detto distribuzione statistica. Ovviamente la somma delle frequenze relative è pari ad uno, perché \( \Sigma _{k}n_{k}= N \)
La figura a fianco mostra ad esempio la distribuzione delle frequenze relative per il numero di risposte esatte, su un totale di 20 domande, nella sezione “Scienze” di un test CISIA per l’ammissione alle facoltà di Ingegneria svoltosi nel 2008.

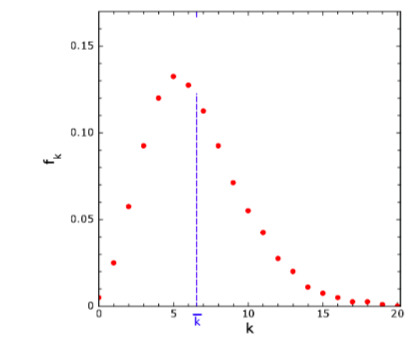
Media e deviazione standard. Il valor medio k, che ci dà una stima del “valore tipico” della variabile k, può essere semplicemente definito come la somma di tutti i risultati divisa per il numero totale di misure, ma un modo alternativo e sicuramente più utile è quella di pesare ciascun valore con la frequenza con cui viene ottenuto, scrivendo

\( \overline{k}=\sum_k f_{k}k \)

Nella distribuzione mostrata in figura, ad esempio, si ha \( \overline{k} \simeq 6,55 \)(indicata dalla linea blu).

Una stima della larghezza di una distribuzione si può invece ottenere calcolando il valor medio della differenza al quadrato dei valori dalla media e prendendono la radice quadrata, parametro che è detto deviazione standard \( \sigma_{k} \) della variabile \( k \):

\( \sigma_{k}=\sqrt \Sigma _{k}f_{k}(k-\overline{k})^{2} \)

5. Istogrammi

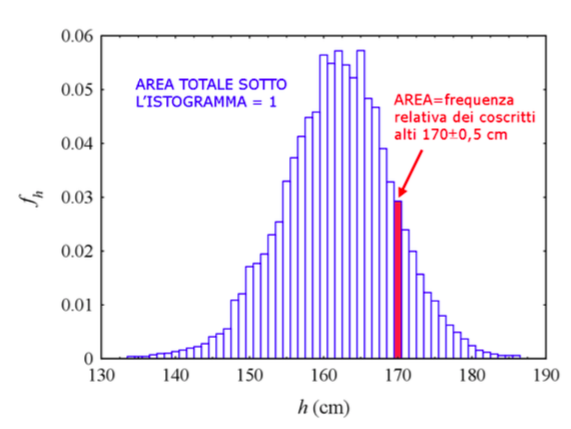
Se la grandezza che consideriamo (chiamiamola ora \( X \)) assume valori continui, ossia tutti i valori in un intervallo dell’asse reale, non ha però senso dare la frequenza di un singolo valore, ma solo la frequenza con cui la variabile cade in un certo intervallo. In questo caso per rappresentare la distribuzione è utile rappresentarla con un istogramma come quello in figura, dove viene mostrata la distribuzione dell’altezza degli italiani (maschi, ovviamente) chiamati alle armi nell’ultimo anno della I guerra mondiale. Qui le frequenze relative a ciascun intervallo sono date delle aree sotto ciascun rettangolino. Quindi l’area sotto l’intero istogramma è ancora pari ad uno.