Il fissaidee
| Sito: | Federica Web Learning - LMS |
| Corso: | Scienze fisiche di base |
| Unit: | Il fissaidee |
| Stampato da: | Utente ospite |
| Data: | martedì, 26 agosto 2025, 20:24 |
1. Moto unidimensionale: posizione, velocità, accelerazione

Seconda tappa
Nel caso di moto unidimensionale la posizione è data semplicemente dalla coordinata lungo la retta, diciamo \( x \); la funzione \( x(t) \) che descrive la posizione \( x \) in funzione del tempo \( t \), prende il nome di equazione oraria.
Un’ulteriore grandezza necessaria per descrivere il moto è la velocità: cominciamo col definire la velocità media: si definisce velocità media nell’intervallo di tempo \( [t_1, t_2] \) il rapporto tra lo spazio percorso tra \( t_1 \) e \( t_2 \) (cioè \( x(t_2) – x(t_1) \) )- e l’intervallo di tempo impiegato a percorrerlo \( (t_2 – t_1) \). In formula:
\( v_{t_1,t_2 }≡ \frac{x(t_2 )-x(t_1 )}{t_2-t_1} \)
Se gli intervalli tendono a zero possiamo ora definire la velocità istantanea all’istante di tempo t1 come la velocità media nell’intervallo di tempo \( [t_1, t_2] \) quando \( t_2 \) si avvicina sempre di più a \( t_1 \) (in linguaggio più matematico quando \( t_2 \) tende a \( t_1 \)). Graficamente, il valore della velocità istantanea sarà dato dal coefficiente angolare della tangente al grafico della legge oraria nell’istante t1.
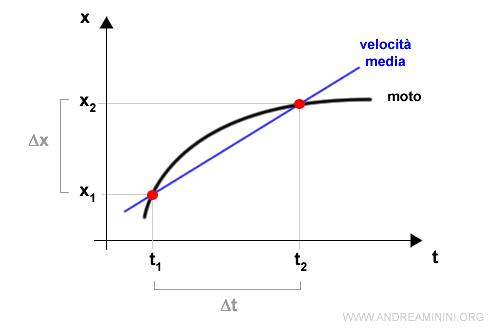
Con una notazione più compatta possiamo ora anche dire che la velocità media è data dal rapporto fra intervalli \( \frac{ \Delta x}{\Delta t} \), mentre quella istantanea dal rapporto degli intervalli infinitesimi \( \frac{dx}{dt} \), identificabile come la derivata di \( x \) rispetto al tempo; viceversa otterremo \( x \) dalla velocità con una operazione di integrazione.
Ad esempio consideriamo un moto con velocità \( v \) costante nel tempo: l’equazione oraria sarà \(x(t) = x0 + v t\)
Per spostarti tra le pagine del fissaidee utilizza le frecce azzurre.
2. Descrivere il movimento
Come varia nel tempo la posizione di un oggetto puntiforme (che non vibra, e non ruota): quali grandezze fisiche ci servono?
Ma prima di tutto: movimento rispetto a cosa? Occorre definire un sistema di riferimento: nello spazio il nostro riferimento saranno ad esempio 3 assi mutuamente ortogonali (terna cartesiana).
3. L'accelerazione
La velocità in generale varierà a sua volta in funzione
del tempo; definiremo pertanto la grandezza accelerazione a.
Cominciamo
col definire l'accelerazione media: si definisce accelerazione media
nell’intervallo di tempo \( [t_1 t_2] \) il rapporto tra la variazione di velocità tra \( t_{1} \)\( t_{2} \) (cioè \(v \)(\( t_{2} \))- \(v \)(\( t_{1} \))) e l'intervallo di tempo (\( t_{2} \)-\( t_{1} \)), in formula:
\( a_{t_1,t_2 }≡ \frac{v(t_2 )-v(t_1 )}{t_2-t_1} \)
Se gli intervalli tendono a zero possiamo ora definire la accelerazione istantanea all’istante di tempo \( t_1 \) come l’accelerazione media nell’intervallo di tempo [\( t_{1} \),\( t_{2} \) ] quando \( t_{2} \) si avvicina sempre di più a \( t_{1} \) (in linguaggio più matematico quando \(t_{2} \) tende a \( t_{1} \))
Anche qui con una notazione più compatta possiamo ora dire che l’accelerazione media è data dal rapporto fra intervalli \( \frac{Dv}{Dt} \), mentre quella istantanea dal rapporto degli intervalli infinitesimi \( \frac{dv}{dt} \), identificabile come la derivata di \( v \) rispetto al tempo, ovvero come la derivata seconda di \( x \) rispetto al tempo; viceversa otterremo \( v \) dall’accelerazione con una operazione di integrazione
Ad esempio consideriamo un moto con accelerazione a costante nel tempo, otterremo
\(v\)\((t)\) = \(v\)0 + \(a t\) e quindi l’equazione oraria \(x\)\((t)\) = \(x\)0 +\(v\)0 \(t\) + ½ \(a t\) 2
Nel sistema internazionale (SI) la posizione si misura in metri \( (\textbf{m}) \), quindi la velocità in metri al secondo \( \textbf{m}/\textbf{s} \) e l’accelerazione in metri al secondo quadrato \( \textbf{m}/\textbf{s}^2 \)
4. Moto nello spazio: grandezze vettoriali
Nello spazio tridimensionale la posizione \( \vec{s} \) di un punto \( \textbf{P} \) non può essere definita da un unico numero: oltre alla distanza di \( \textbf{P} \) dall’origine degli assi, dovremo specificare la direzione e il verso che lo caratterizzano. Le grandezze di questo tipo (oltre a posizione anche ad esempio velocità e accelerazione, che ne derivano) sono dette vettori.
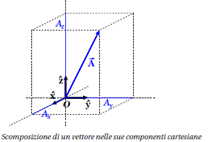
Una qualunque quantità \( \vec{A} \), dotata di orientamento e lunghezza può essere identificata attraverso le sue tre componenti \( \textbf{A}_x;\textbf{A}_y;\textbf{A}_z \) lungo le tre direzioni cartesiane
\( \vec{A} = A_x \hat{x} + A_y \hat{y} + A_z \hat{z} \)
Le definizioni di velocità ed accelerazione, media ed istantanea devono essere quindi generalizzate per tenere conto della natura vettoriale di queste grandezze:
\( \vec{v} _{[t_1,t_2]}≡ \frac{\vec{s}(t_2)- \vec{s}(t_1)}{t_2-t_1} \)
\( \vec{a} _{[t_1,t_2]}≡ \frac{\vec{v}(t_2)- \vec{v}(t_1)}{t_2-t_1} \)
La velocità istantanea risulta sempre tangente alla traiettoria percorsa dall’oggetto.
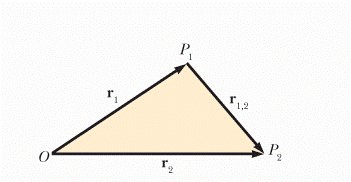
Moto relativo: Dati 2 punti \( \textbf{P_1} \) e \( \textbf{P_2} \) possiamo definire la posizione di \( \textbf{P_1} \) rispetto a \( \textbf{P_2} \) usando la differenza fra i vettori come mostrato nella figura:
Velocità ed accelerazione relative si definiscono allo stesso modo come differenza rispettivamente delle velocità ed accelerazioni.
5. Moto circolare uniforme
Definiamo moto circolare uniforme quello che avviene lungo una circonferenza con modulo della velocità costante nel tempo. Come nel moto rettilineo uniforme, anche in quello circolare uniforme vengono percorsi spazi uguali in tempi uguali, tuttavia, mentre nel moto rettilineo uniforme l’accelerazione è nulla, in quello circolare la velocità cambia continuamente nel tempo e quindi l’accelerazione è sempre diversa da zero. Specificatamente vale zero la componente tangenziale dell’accelerazione (che ha la stessa direzione della velocità istantanea e riflette la variazione del modulo della velocità), mentre è sempre diversa da zero la componente normale dell’accelerazione (che è appunto perpendicolare alla tangente, e quindi diretta lungo il raggio, e che riflette la variazione in direzione del vettore velocità).
Periodo, velocità angolare e frequenza. Il modulo della velocità sarà dato dal rapporto tra la lunghezza del percorso fatto in un giro cioè \( 2 \pi r \), dove \( r \) è il raggio della circonferenza, e il tempo impiegato a compiere il giro, che si chiama periodo \( \textbf{T} \) del moto; quindi sarà:
\( v= \frac{2 \pi r}{\textbf{T}} \)
La grandezza \( \frac{2 \pi r}{\textbf{T}} \) rappresenta la velocità angolare ω del punto; infatti, nel periodo \( \textbf{T} \) il punto avrà percorso un angolo giro, cioè \( 2 \pi \) radianti. Perciò si avrà \( v= \omega r \).
La frequenza è definita come l’inverso del periodo \( v≡ \frac{1}{\textbf{T}} \) e si misura in \( \textbf{Hz} \) cioè \( 1 /\textbf{s} \). Ci dice quanti cicli oppure quante rotazioni complete, oppure quante oscillazioni ci sono in un secondo.
La velocità angolare e la frequenza hanno le stesse dimensioni, ovvero l’inverso di un tempo:
\( \omega = \frac{2 \pi }{\textbf{T}} = 2 \pi v \)
L’accelerazione come detto sopra è costante nel moto circolare uniforme e sempre diretta lungo il raggio: il valore del suo modulo è: