Il fissaidee
| Site: | Federica Web Learning - LMS |
| Course: | Scienze fisiche di base |
| Unit: | Il fissaidee |
| Printed by: | Guest user |
| Date: | Tuesday, 26 August 2025, 8:24 PM |
Table of contents
- 1. Forze: cosa sono?
- 2. Corpi elastici
- 3. Stato di un moto “naturale” di un corpo e primo principio
- 4. Le forze cambiano lo stato di moto: il secondo principio
- 5. Forza come interazione: il terzo principio
- 6. La forza di attrito
- 7. Gli esperimenti
- 8. Quantità di moto
- 9. L'impulso e la sua relazione con la quantità di moto
- 10. Lavoro
- 11. Forze conservative
- 12. Energia cinetica
- 13. Energia potenziale
- 14. L'energia meccanica e la sua conservazione
1. Forze: cosa sono?

Terza tappa
Possiamo riconoscere una forza attraverso i suoi effetti. Questi possono essere di due tipi:
Deformazione degli oggetti

La palla è deformata perché l’atleta applica una forza
Variazione dello stato di moto degli oggetti (cioè accelerazione)
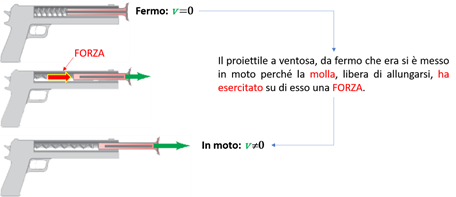
Spesso i due effetti coesistono, ma la deformazione è troppo rapida (oppure piccola) perché possa essere osservata a occhio nudo:
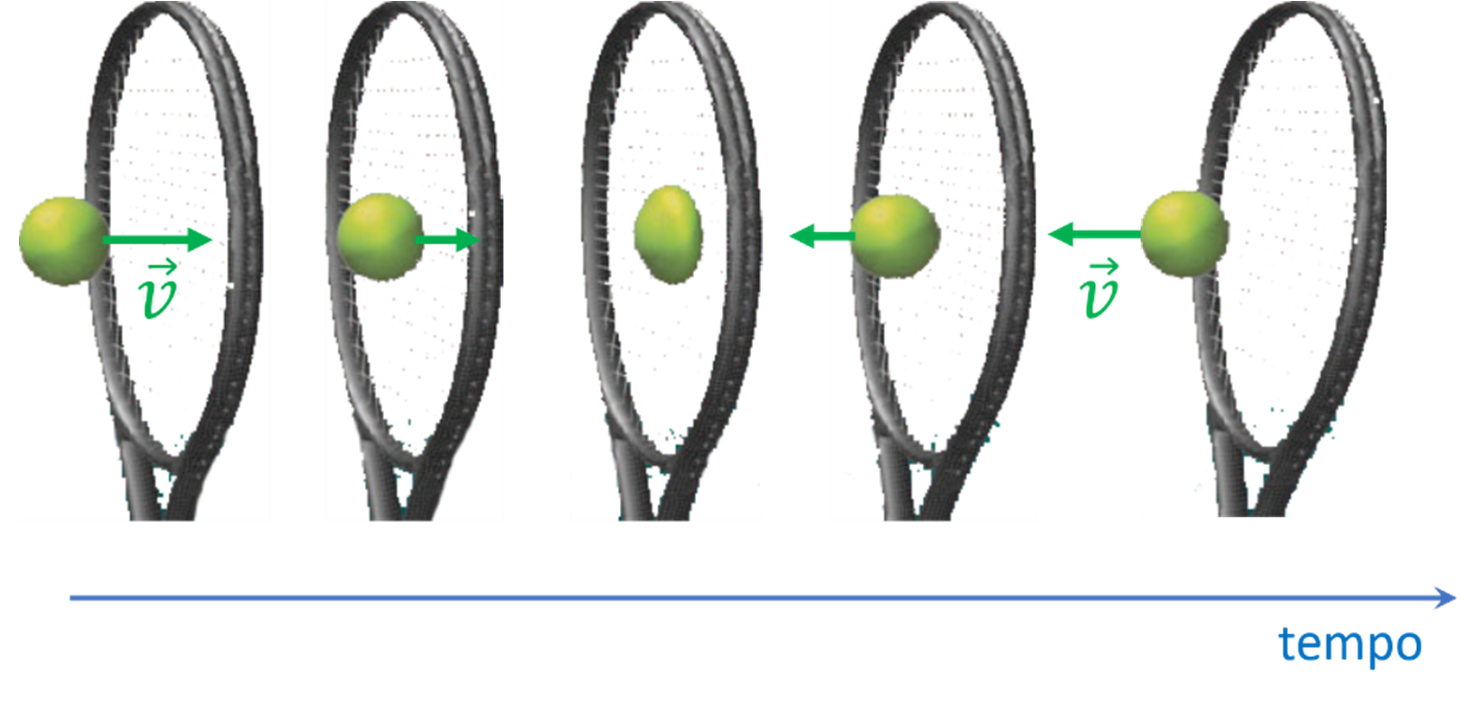
Una palla da tennis colpita dalla racchetta (la quale esercita quindi sulla palla una forza) cambia la propria velocità (cioè subisce un’accelerazione).
Durante il breve intervallo di tempo di contatto con la racchetta la palla si deforma.
Per spostarti tra le pagine del fissaidee utilizza le frecce azzurre.
2. Corpi elastici
Alcuni corpi, detti “elastici”, si deformano in maniera regolare quando sono sottoposti all’azione di una forza. Ad esempio, nella figura in basso, una molla sottoposta alla forza di due pesetti uguali si allunga (in riferimento alla sua lunghezza “naturale”, cioè quando non è sottoposta a forze) del doppio rispetto a quando è sottoposta alla forza di un solo pesetto.
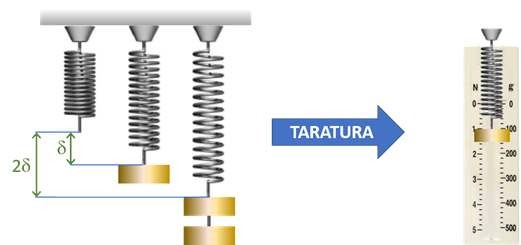
Questa “regolarità della deformazione” dei corpi elastici può essere utilizzata per costruire una tipologia di dispositivi atti a misurare le forze, detti “dinamometri”. È sufficiente dotare la molla di uno “sfondo fisso” recante una scala graduata, definita mediante la successiva applicazione di un numero crescente di pesetti noti e uguali tra loro. Questo procedimento si definisce “Taratura”.
3. Stato di un moto “naturale” di un corpo e primo principio
L’esperienza quotidiana ci conduce erroneamente e ritenere che la “tendenza naturale” dei corpi sia la quiete. Nel senso che un corpo, in assenza di qualcosa o qualcuno che lo costringa a permanere in moto, inevitabilmente si ferma! Ad esempio, una macchinina giocattolo lanciata lungo un pavimento orizzontale, dopo aver percorso un certo spazio si ferma. Ma anche un’automobile vera, lanciata a una certa velocità su una strada piana e rettilinea, una volta messa “in folle” finisce inevitabilmente col fermarsi prima o poi. O ancora: una palla da calcio, calciata orizzontalmente in modo che rotoli sul piano orizzontale, magari arriverà molto lontano, ma certamente finirà col fermarsi!In tutti questi esempi l’oggetto in moto in realtà non è libero di muoversi secondo la sua “tendenza naturale” in quanto è presente l’azione di un tipo di forza piuttosto “subdola” (nel senso che non è di immediato riconoscimento) che chiamiamo attrito. Come hai avuto modo di apprendere nella lezione, Galilei ideò una serie di esperimenti che gli suggerirono quale sia la tendenza naturale di un corpo: permanere nel suo stato di moto. Cioè, se è fermo, “vorrebbe” continuare a restare fermo; se si sta muovendo, “vorrebbe” continuare a muoversi mantenendo invariata la velocità.
Naturalmente i corpi inanimati non hanno “volontà”, motivo per cui alcuni verbi nelle frasi precedenti sono tra virgolette! La legge della Natura che governa il moto libero di un corpo (cioè non sottoposto a forze, oppure sottoposto solo all’azione di più forze la cui risultante è nulla) è espressa dal primo principio della dinamica, detto anche principio di inerzia: “Un corpo sul quale non agiscono forze, oppure agiscono in modo tale che la forza risultante è nulla, se è fermo continua a restare fermo, se è in moto continua a muoversi con la stessa velocità”. Attenzione: stessa velocità significa stesso modulo e anche stessa direzione. Quindi, alla luce del principio d’inerzia, possiamo dire che esiste un tipo di moto “speciale”, nel senso che è quello che i corpi “vorrebbero” fare se fossero lasciati liberi di farlo: il moto rettilineo uniforme!
4. Le forze cambiano lo stato di moto: il secondo principio
La situazione di un corpo presa in considerazione per il primo principio (nessuna forza agente, oppure sul corpo agiscono solo forze la cui risultante è nulla) è decisamente rara. Nella pratica è di estremo interesse sapere come si comporta un corpo quando non è nelle condizioni per cui vale il principio di inerzia. Questo ce lo dice il secondo principio della dinamica, il quale afferma che un corpo sottoposto a una o più forze si muove con un’accelerazione, il cui modulo è proporzionale al modulo della risultante delle forze e la cui direzione e verso coincidono con quelli della suddetta risultante. In formula possiamo scrivere:
\( \vec{a} \propto \vec{F}_{ris} \)
Dove il simbolo “∝” si legge “è proporzionale a”. Come sai, la proporzionalità (diretta) equivale a dire che una grandezza è uguale all’altra moltiplicata per una costante. In questo caso la costante, determinata sperimentalmente, è il reciproco della massa del corpo, per cui il secondo principio si può scrive:
\( \vec{a} = \frac{1}{\textbf{m}} \vec{F}_{ris} \)
Questo modo di scriverlo evidenzia il ruolo della massa come ciò che “ostacola” l’accelerazione (e perciò è detta “inerziale”): a parità di forza, maggiore è la massa, minore è l’accelerazione. Una forma più familiare per il secondo principio è la seguente:
\( \vec{F}_{ris} = {\textbf{m}} \vec{a} \)
Lo schema seguente può esserti utile per ricordare e mettere in relazione tra loro primo e secondo principio:
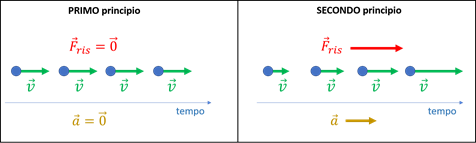
5. Forza come interazione: il terzo principio
Se esamini qualunque esempio concreto di forza che possa venirti in mente, ti accorgerai che una forza agente su un corpo (chiamiamolo A) è sempre esercitata da un altro corpo (chiamiamolo B). Ad esempio, la forza peso che agisce su di te (che è responsabile del fatto che ti senti pressato sui piedi se sei in piedi o sul didietro se stai seduto) è esercitata dalla Terra. Ebbene, un aspetto molto importante di questo carattere “binario” delle forze è che i due oggetti, A e B, hanno un ruolo del tutto “simmetrico”. In altri termini, se A esercita una certa forza su B, anche B esercita su A la medesima forza, solo con verso opposto! È il terzo principio della dinamica, detto anche di azione e reazione. Questa denominazione può essere un po’ fuorviante perché induce a pensare che un corpo abbia un ruolo “attivo” (azione) e che l’altro subisca l’azione e in conseguenza reagisca! In realtà il terzo principio ci dice che non c’è mai un (solo) corpo che esercita una forza su un altro; ce ne sono sempre due che interagiscono (pensa all’etimologia di questo termine…), cioè esercitano reciprocamente un’azione l’uno sull’altro, in maniera perfettamente simmetrica.6. La forza di attrito
Quando due corpi scivolano (o si tenta di farli scivolare) l’uno sull’altro, tra essi si esercita una forza, dovuta al contatto tra le superfici e parallela alle superfici stesse, detta forza d’attrito. Tale forza è onnipresente nella nostra vita quotidiana e, sebbene sia di ostacolo al moto, è in realtà indispensabile per compiere delle azioni apparentemente banali, come ad esempio camminare (pensa a cosa succede se cerchi di camminare su una lastra di ghiaccio, situazione nella quale l’attrito tra le suole delle tue scarpe e la superficie di appoggio è molto ridotto).
Consideriamo la situazione tipica illustrata in figura: Ettore cerca di far scivolare una scatola lungo il pavimento e per far ciò applica la forza \( \vec{F} \). Il pavimento esercita sulla scatola una forza di attrito (indicata con \( \vec{F}_a \) in figura) che è diretta in verso opposto alla velocità di scorrimento della scatola (se questa si muove); oppure in verso opposto al tentativo di Ettore di far muovere la scatola, cioè in verso opposto alla forza applicata \( \vec{F} \).
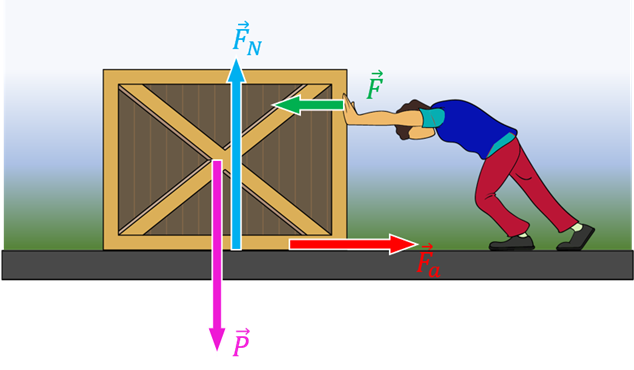
7. Gli esperimenti
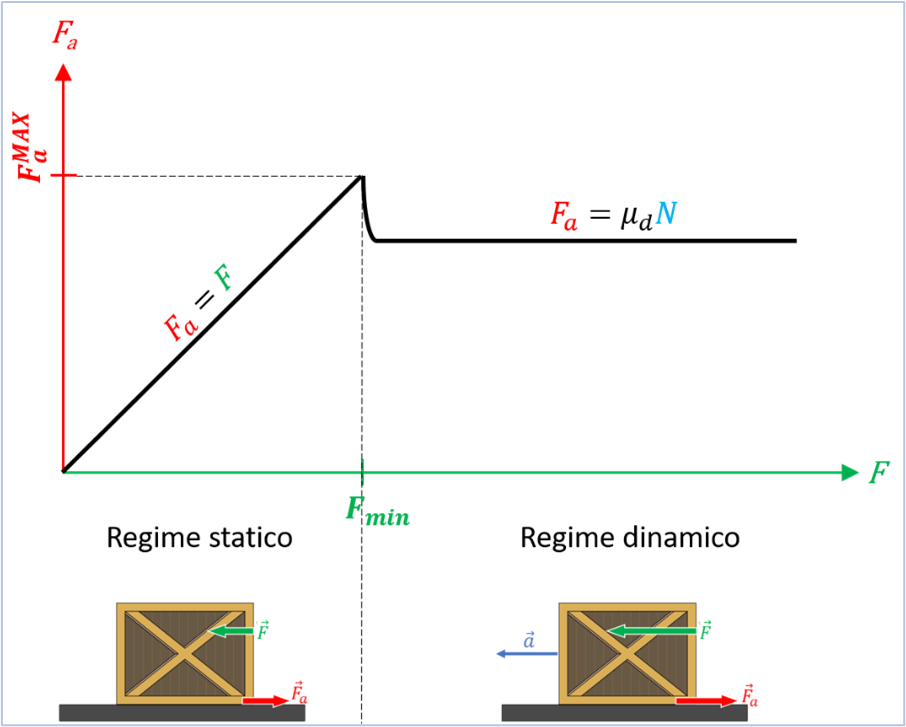
Gli esperimenti mostrano che la scatola non si muove finché il modulo della forza applicata non supera un certo valore minimo \( F_{min} \). Se invece \( F>F_{min} \) la scatola si muove, ma il suo moto è comunque ostacolato dal contatto col pavimento.
Questa situazione è illustrata in dettaglio nella figura a fianco. In particolare, nel “Regime statico”, via via che la forza applicata \( \vec{F} \) aumenta in modulo, aumenta anche la forza orizzontale tra pavimento e scatola \( \vec{F}_a \) (che chiameremo in questo caso di attrito statico), mantenendosi pari in modulo alla forza applicata, cosicché la risultante è nulla e la scatola rimane in equilibrio statico. Esiste però un valore massimo che può assumere la forza di attrito statico (\( \vec{F}_a^{MAX} \)) per cui, allorché la forza applicata supera tale valore, la scatola comincia a muoversi e nel contempo la forza di attrito si stabilizza su un valore leggermente inferiore a \( \vec{F}_a^{MAX} \): il moto entra quindi nel “Regime dinamico”.
Gli esperimenti mostrano anche che sia il valore \( \vec{F}_a^{MAX} \) del massimo attrito statico, che quello \( \vec{F}_a \) dell’attrito dinamico, dipendono solo dalla natura delle superfici in contatto e dalla forza con cui queste sono “pressate” l’una sull’altra, cioè dalla forza normale \( F_N \) (vedi la prima figura di questa sezione), il cui modulo è pari a quello del peso della scatola se il pavimento è orizzontale. In particolare si trova che \( F_a^{MAX}=μ_s F_N \) e \(F_a=μ_d F_N \). Le due quantità adimensionali \( μ_s \) e \( μ_d \), dette rispettivamente coefficiente di attrito statico e coefficiente di attrito dinamico, dipendono esclusivamente dalla natura delle superfici in contatto e soddisfano alla relazione \( 0<μ_d<μ_s<1 \).
8. Quantità di moto
È utile associare a un corpo in moto una grandezza vettoriale, detta quantità di moto, definita come il prodotto della sua massa per la velocità, \( \vec{p}= \vec{mv} \). Nel S.I. si misura in kg×m×s-1 . Si tratta di una grandezza molto importante e utile nello studio del moto di un corpo, soprattutto quando questo interagisce con altri corpi. Infatti, \( \vec{p} \) è una grandezza additiva (cioè, la quantità di moto di un insieme di corpi è pari alla somma vettoriale delle quantità di moto dei singoli) e, quando più corpi interagiscono tra loro mediante forze, si “scambiano” quantità di moto. Questo modo di vedere le cose è particolarmente utile nel caso degli urti tra due corpi.
La quantità di moto di un corpo può variare a causa dell’azione di una o più forze agenti su di esso. Nel caso semplice di una forza costante \( \vec{F} \) che agisce sul corpo per un intervallo di tempo \( \Delta t \), la variazione della quantità di moto è data dalla formula \( \Delta \vec{p}= \vec{F} \Delta t \). Questa relazione è equivalente alla seconda legge di Newton. Possiamo verificarlo sostituendo in essa la definizione di \( \vec{p} \), ottenendo (nell’ipotesi che la massa del corpo non vari): \( m \Delta \vec{v}= \vec{F} \Delta t \). Da qui, dividendo membro a membro per \( \Delta t \), si ha: \( m \frac{\Delta \vec{v}}{\Delta t} = \vec{F} \). Quando l’intervallo di tempo diventa molto piccolo (tende a zero), il rapporto tra la variazione di velocità e l’intervallo di tempo tende – per definizione – all’accelerazione istantanea, per cui si ottiene \( m \vec{a} = \vec{F} \), che è la seconda legge di Newton.
9. L'impulso e la sua relazione con la quantità di moto
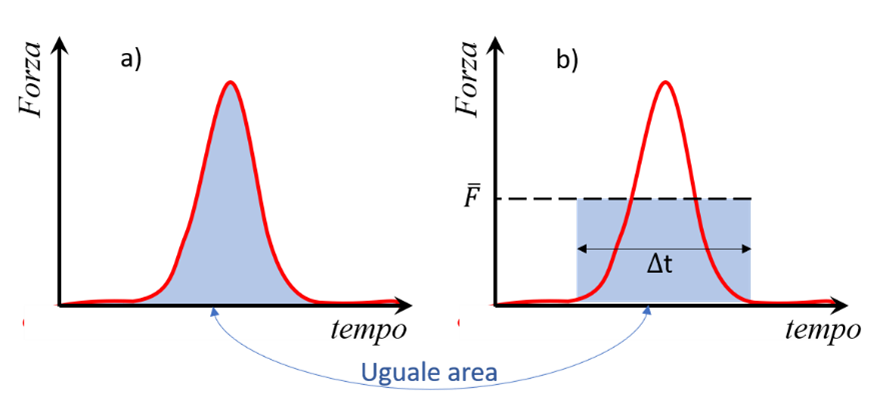
In pratica sono molto frequenti i casi in cui la forza agente sul corpo non è costante. Tra questi, particolare rilievo è assunto dalle forze cosiddette “impulsive”, cioè quelle che agiscono per un intervallo di tempo molto breve ma con intensità elevata: pensiamo ad esempio alla forza agente su una palla da tennis durante l’impatto con la racchetta, oppure su una palla da calcio che venga calciata. Un andamento temporale tipico di forze del genere è mostrato nella parte a) della figura. In questi casi è molto difficile descrivere come la forza varia nel tempo, data l’estrema rapidità del fenomeno; tuttavia a fini pratici è sufficiente conoscere il valore medio del modulo della forza (indichiamolo col simbolo \( \overline{F} \)) nell’intervallo di tempo \( \Delta t \) durante il quale essa agisce. Con riferimento alla figura, \( \overline{F} \) è definita come il valore della forza per cui l’area del rettangolo colorato nella parte b) è uguale all’area sotto il grafico Forza/tempo nella parte a). In questo contesto è utile introdurre una nuova grandezza associata alla forza, detta impulso (simbolo \( I \)), che tiene conto di quanto essa è intensa e di quanto a lungo agisce: \( I \) = “area compresa sotto il grafico forza/tempo” (area colorata nella parte a della figura). Ricordando la definizione di valor medio della forza, l’impulso (che è una grandezza vettoriale avente la medesima direzione e verso della forza) può essere espresso in modulo come \( I=\overline{F} \Delta t \).
L’introduzione del concetto di impulso permette di esprimere in maniera generale la relazione tra la variazione della quantità di moto del corpo e le caratteristiche della forza che provoca tale variazione, mediante una legge nota come teorema dell’impulso, la quale afferma che la variazione della quantità di moto di un corpo è uguale all’impulso della forza che agisce su di esso: \( \Delta \vec{p} =\vec{I} \).
Tutte le precedenti considerazioni, fatte per il caso di una sola forza agente, rimangono valide nel caso in cui sul corpo agiscano contemporaneamente più forze, purché si consideri la forza risultante di queste.
10. Lavoro
Il termine “lavoro” nel linguaggio della fisica ha un significato differente rispetto al linguaggio comune, anche se in entrambi i casi ha a che fare con l’azione delle forze. Infatti, nel linguaggio comune “lavoro” è spesso sinonimo di “fatica” e, come sai, ci si può molto affaticare anche stando fermi; in fisica, invece, condizione necessaria perché possa esserci lavoro è che ci sia spostamento. Per chiarirlo consideriamo la situazione mostrata in figura.
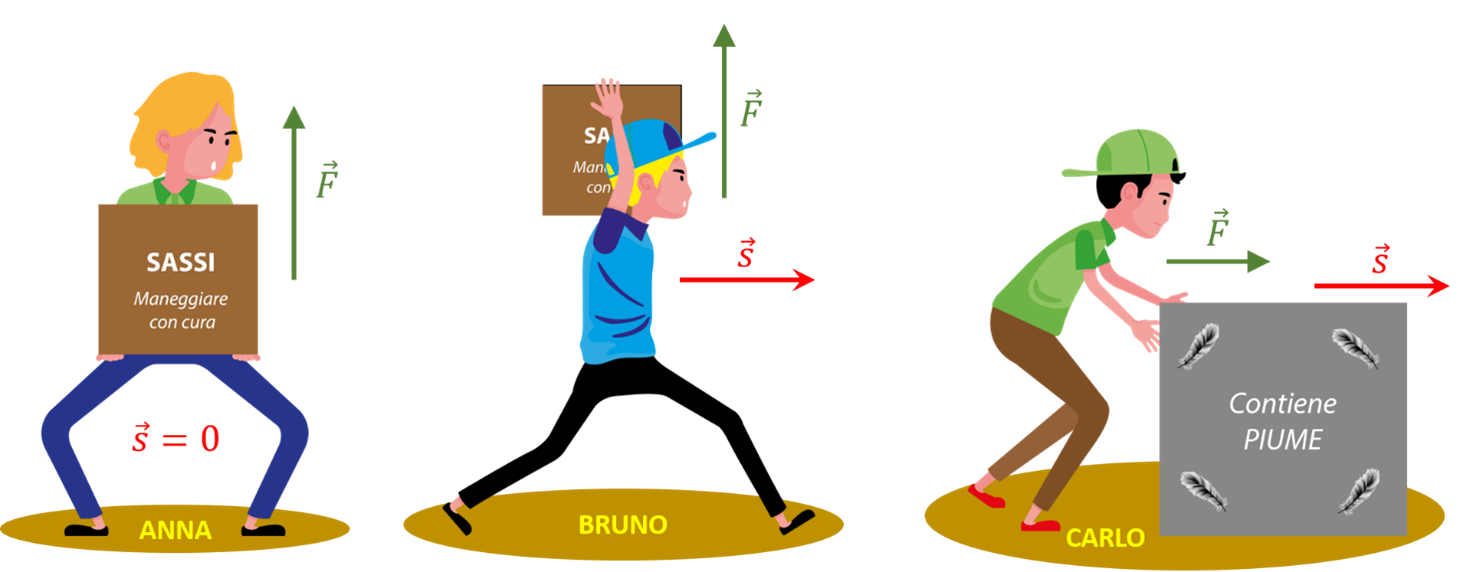
Anna applica una forza \( \vec{F} \) diretta verso l’alto a una pesante scatola per sostenerla ferma; Bruno applica la medesima forza alla stessa scatola, che ha in spalla, per trasportarla orizzontalmente; Carlo applica alla sua scatola una forza diretta orizzontalmente per spostarla lungo il pavimento. Certamente tutti e tre si “affaticano” e, pensando al contenuto delle scatole, non è difficile immaginare che Anna e Bruno compiano un “lavoraccio”, mentre Carlo probabilmente fatica molto meno. Ebbene, dal punto di vista della fisica, l’unico dei tre che compie lavoro, mediante la forza che applica alla scatola, è Carlo!
Infatti, in fisica una forza applicata a un corpo compie lavoro L solo se il corpo si sposta e se lo spostamento NON è perpendicolare alla forza. Quindi il lavoro compiuto da Anna è nullo perché la scatola rimane ferma nonostante lei applichi una notevole forza per mantenerla tra le braccia; anche quello compiuto da Bruno è nullo perché la scatola sulla quale è applicata la forza si sposta, ma lo fa in direzione perpendicolare alla forza stessa; Carlo, infine, compie lavoro perché la scatola si sposta e lo fa in una direzione che non è perpendicolare allo spostamento, anzi nel caso mostrato in figura è parallela a essa.
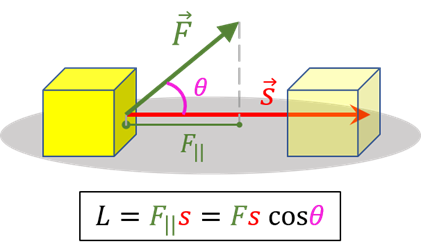
La definizione quantitativa del lavoro L compiuto da una forza costante \( \vec{F} \) è illustrata nella figura a fianco: esso è pari al prodotto della componente della forza lungo la direzione dello spostamento \( (F_{||}) \) per il modulo dello spostamento stesso. Esprimendo \( F_{||} \) mediante il coseno dell’angolo che il vettore forza forma con lo spostamento, si ottiene l’ultima espressione in figura.
11. Forze conservative
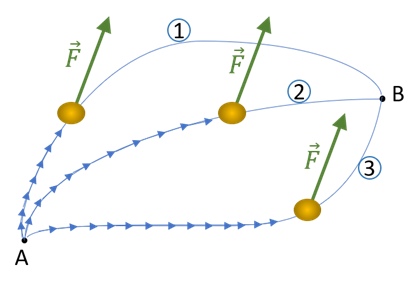
Quando un corpo si sposta da un punto A a un punto B sotto l’azione di una forza, il lavoro compiuto da questa potrebbe dipendere dal percorso compiuto per andare da A a B, oppure potrebbe dipendere SOLO da A e B, e non dallo specifico percorso fatto dal corpo (in figura sono esemplificati tre possibili percorsi). In questo secondo caso, la forza è detta conservativa, mentre se il lavoro dipende anche dal percorso è detta non conservativa. Come vedremo fra breve, le forze conservative sono particolarmente importanti in quanto è possibile associare a un corpo che si muova sotto la loro azione una forma di energia detta energia potenziale.
12. Energia cinetica
Strettamente connesso al concetto di lavoro c’è quello di energia, che possiamo definire come la capacità di compiere lavoro. Sia il lavoro che l’energia nel S.I. si misurano in joule (simbolo \( \textbf{J} \)). Un corpo può avere capacità di compiere lavoro per vari motivi: uno dei più importanti e comuni è perché si muove. È quindi utile considerare una forma di energia associata al movimento, detta energia cinetica, simbolo \( K \), che dipende dalla massa \( m \) del corpo e dal modulo \( v \) della sua velocità nel modo seguente: \( K=\frac12 mv^2 \). Quando un corpo si muove sotto l’azione di una o più forze, la sua energia cinetica può variare e – fatto molto importante – tale variazione \( (∆K) \) è uguale al lavoro compiuto dalla risultante delle forze agenti sul corpo stesso: \( ∆K=L_{ris} \). Questa proprietà prende il nome di teorema dell’energia cinetica (o anche teorema lavoro-energia).
13. Energia potenziale
Un’altra forma in cui si concretizza la capacità di un corpo di compiere lavoro è l’energia potenziale. Questa, come anticipato prima, è associata alle forze conservative ed è un tipo di energia che dipende dalla posizione reciproca di un insieme di corpi (almeno due) che interagiscono mediante una forza conservativa. L’esempio più comune di energia potenziale è quella posseduta da un corpo di massa \( m \) posto ad altezza \( h \) rispetto a un piano di riferimento arbitrario, in prossimità della superficie terrestre. Questa capacità di compiere lavoro, detta energia potenziale gravitazionale, di solito si indica con la lettera \( U_G \), ed è dovuta all’interazione del corpo con la Terra per mezzo della forza gravitazionale. Il suo valore è dato dall’espressione \( U_G=mgh \), dove \( g \) è l’accelerazione di gravità in prossimità della superficie terrestre.
Un altro importante caso di forza conservativa è la forza elastica (quella descritta dalla legge di Hooke per le molle). L’esempio tipico è quello di una molla di costante elastica \( k \) e lunghezza di equilibrio, in assenza di forze applicate, pari a \( l_0 \). Se la molla viene compressa oppure allungata fino a farle assumere una lunghezza \( l \), in tale condizione essa avrà “immagazzinato” capacità di compiere lavoro, sotto forma di energia potenziale elastica, pari a \( U_E=\frac12 k(l-l_0 )^2 \) .
14. L'energia meccanica e la sua conservazione
Concludiamo ricordando che, quando un corpo si muove sotto l’azione di forze conservative, a esso è possibile associare una forma complessiva di energia, detta energia meccanica, pari alla somma dell’energia cinetica e di quella potenziale: \( E=K+U \). In tal caso, la legge di conservazione dell’energia meccanica stabilisce che, allorché durante il moto del corpo la sua energia si trasforma dall’una all’altra forma, il totale (cioè il valore di \( E \)) rimane costante. Questa importante proprietà non è valida in presenza di forze non conservative (che peraltro non consentono neanche di introdurre l’energia potenziale). L’esempio più noto e importante in pratica di forza non conservativa è costituito dalla forza di attrito, nelle sue varie forme (attrito radente, volvente, viscoso…).