Il fissaidee

Sito:	Federica Web Learning - LMS
Corso:	Scienze fisiche di base
Unit:	Il fissaidee

Stampato da:	Utente ospite
Data:	martedì, 1 luglio 2025, 01:39

1. Trasformazioni dell'energia, potenza

Quarta tappa

Nella terza tappa del Fissaidee abbiamo avuto modo di ricordare come l’energia meccanica si possa inter-convertire tra le due forme sin lì esaminate: cinetica e potenziale (gravitazionale o elastica). In effetti l’energia può assumere diverse altre forme, che avremo modo di vedere più avanti, e tra queste si può trasformare (rifletti sull’etimologia di questo termine…). Allorché si ha una conversione di una certa quantità di energia da una forma all’altra, un parametro molto importante anche a fini pratici è la “rapidità” con cui la conversione avviene, cioè il rapporto tra l’energia \( ∆E \) trasformata in un dato intervallo di tempo \( ∆t \) e l’intervallo di tempo stesso: \( P=\frac{∆E}{∆t} \); tale grandezza è detta potenza è si misura in watt (simbolo \( \textbf{W} \)). Dalla definizione di potenza segue che \( 1\textbf{W} \)=\( \frac{1\textbf{J}}{1\textbf{s}} \)

Per spostarti tra le pagine del fissaidee utilizza le frecce azzurre.

2. Esempio

Ad esempio, una lampada elettrica di potenza pari a \( 10 \textbf{W} \), ogni secondo trasforma in luce (e in energia termica) \( 10 \textbf{J} \) di energia elettrica. Oppure, altro esempio: il motore di un’automobile che funziona alla potenza di \( 60 \textbf{kW} \), ogni secondo trasforma \( 60.000 \textbf{J} \) di energia chimica del carburante in varie altre forme, tra le quali:

energia meccanica (l’automobile aumenta la velocità e/o sale un pendio);
energia termica (la temperatura delle varie componenti del motore aumenta e una notevole quantità di calore viene ceduta all’ambiente);
energia elettrica (utilizzata dai vari dispositivi elettrici del veicolo).

3. \( P= \vec{F} \bullet \vec{v} \)

Oltre che alla inter-conversione dell’energia tra le sue varie forme, il medesimo concetto di potenza si applica allo stesso modo anche alla rapidità di esecuzione del lavoro da parte delle forze. In questo caso la potenza è:

\( P=(lavoro\, compiuto)/(intervallo\, di\, tempo\, impiegato). \)

Nel caso di forze agenti su un punto materiale di massa data, è facile dimostrare che \( P= \vec{F} \bullet \vec{v} \), dove \( \vec{v} \) è la velocità del punto ed \( \vec{F} \) è la risultante delle forze agenti su di esso.

4. Cavallo vapore

Un’altra unità di misura per la potenza, non appartenente al S.I. ma molto utilizzata specialmente in ambito industriale, è il cavallo vapore (simbolo CV) che corrisponde a poco più di \( 735 \textbf{W} \). Si tratta di un’eredità della rivoluzione industriale: via via che i “motori animali” (cavalli, asini e simili) venivano rimpiazzati dai motori a vapore, risultava utile esprimere la capacità di compiere lavoro di questi ultimi (cioè la loro potenza) mediante un’unità di misura che permettesse agli utenti di fare un rapido raffronto con gli animali sino a quel momento utilizzati come unica fonte motrice.

5. Il kilowattora

Concludiamo ricordando un’unità di misura non appartenente al S.I., il cui nome potrebbe ingannevolmente ricordare la potenza, mentre si riferisce all’energia: il kilowattora, simbolo kWh. Questa unità, molto utilizzata nella pratica (ad esempio nelle bollette di pagamento dell’energia elettrica domestica), ha la sua definizione contenuta nel nome: un kilowattora equivale all’energia trasformata nell’intervallo di tempo di un’ora da un dispositivo avente la potenza di un kiloWatt. Quindi, dalla definizione di potenza, e ricordando la conversione da ore a secondi, otteniamo:

\( E=P×∆t=103 \textbf{W}×3.6×10^3 \textbf{s} =3.6×10^6 \textbf{Ws} \);

sicchè \( 1 \textbf{kWh} =3.6 \textbf{MJ} \).

6. Moti periodici

Si dice periodico un moto (o più in generale un fenomeno) che si ripete in ciascuna sua “fase” dopo un fissato intervallo di tempo; quest’ultimo prende il nome di periodo del fenomeno e, nel S.I., si misura in secondi. Ad esempio, l’alternarsi delle fasi lunari è un fenomeno periodico il cui periodo è pari a circa 28 giorni. L’oscillazione di un corpo sospeso mediante una funicella (pendolo) si ripete con un periodo che dipende dalla lunghezza della funicella e dall’accelerazione di gravità del luogo. La rotazione di un disco musicale in vinile, cosiddetto “33 giri”, è un moto periodico con periodo pari a 1.8 s (la denominazione si riferisce al fatto che il disco compie circa 33 giri al minuto; per la precisione 33.3).

7. La frequenza

Un altro parametro caratteristico dei fenomeni periodici è la frequenza, cioè il numero di volte che il fenomeno si ripete nell’unità di tempo (la quale, naturalmente, può anche non essere un numero intero). La relazione tra frequenza (\( f \)) e periodo (\( \textbf{T} \)) è di proporzionalità inversa: \( f=\frac{1}{\textbf{T}} \). Da tale relazione segue che l’unità di misura della frequenza nel S.I. è il reciproco di quella del periodo, cioè \( \textbf{s}^{-1} \), e prende il nome di hertz (simbolo Hz): \( 1 \textbf{Hz}=1 \textbf{s}^{-1} \).

8. Fenomeni periodici

È importante osservare che i fenomeni periodici hanno rivestito (e rivestono tuttora) un ruolo fondamentale nell’individuazione dei metodi, e nella realizzazione degli strumenti, per la misura del tempo. Tale ruolo è stato inizialmente svolto solo da fenomeni naturali (si pensi ai fenomeni astronomici che sono alla base delle unità di misura “giorno” e “anno”); da alcuni secoli, invece, in particolare dai tempi di Galilei, si fa uso di fenomeni periodici intenzionalmente allestiti, grazie alla comprensione delle leggi che li governano: l’esempio principe (ancorché tecnologicamente superato) è quello del pendolo, ampiamente utilizzato nei vecchi orologi.

9. Moto armonico

Tra le molteplici tipologie di moti periodici ce n’è una che ha grandissima rilevanza: quella dei moti armonici (detti anche oscillazioni armoniche). Un moto è armonico quando la posizione del corpo (\( s \)) in funzione del tempo (\( t \)) è descritta da una funzione di tipo sinusoidale (o cosinusoidale), che nel caso più semplice assume la forma \( s=A\) \(sen(2π\frac{t}{\textbf{T}}) \). Come si può facilmente verificare (ricordando le proprietà del seno, e tenendo presente che il suo argomento va espresso in radianti) questa funzione è periodica con periodo pari a \( \textbf{T} \). La costante A che moltiplica la funzione seno è detta ampiezza del moto e rappresenta il massimo scostamento del corpo rispetto alla posizione di equilibrio (ad esempio il punto più basso della traiettoria, nel caso di un pendolo semplice).

10. Costante elastica

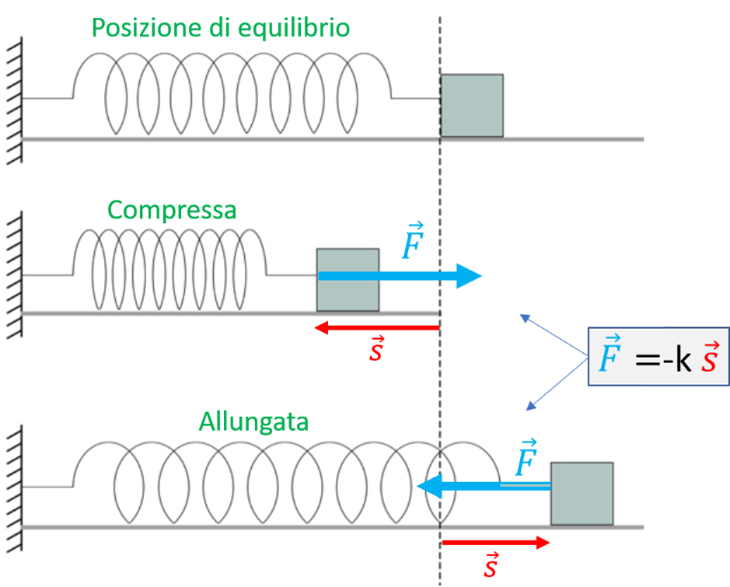
Dal punto di vista dinamico (cioè delle cause che lo determinano) un corpo compie un moto armonico quando è soggetto a una forza che è proporzionale allo spostamento dalla posizione di equilibrio e avente sempre verso opposto allo spostamento stesso (le forze dotate di quest’ultima caratteristica sono dette “di richiamo”). L’esempio più diretto è quello di una massa attaccata all’estremità di una molla, il cui estremo è fissato a una parete. Come si può vedere chiaramente in figura, la forza \( \vec{F} \) esercitata dalla molla, è opposta alla variazione di posizione della massa rispetto alla posizione di equilibrio, sia quando la molla è compressa che quando è allungata. Inoltre (legge di Hooke) il modulo della forza è proporzionale al modulo dello spostamento e la costante di proporzionalità k è un parametro caratteristico della molla, detta costante elastica.

11. Isocronismo delle piccole oscillazioni

Nel caso del sistema massa-molla, la forza esercitata dalla molla sulla massa è proporzionale allo spostamento dalla posizione di equilibrio, qualunque sia il modulo di tale spostamento (sia pure entro certi limiti molto ampi, oltre i quali la molla cessa di comportarsi in maniera “ideale” e si può deformare in maniera permanente). Esistono però numerosi sistemi meccanici nei quali il corpo è soggetto a una forza di richiamo che non è strettamente proporzionale allo spostamento dalla posizione di equilibrio. Alcuni esempi sono mostrati in figura: un pendolo semplice, una pallina libera di rotolare in prossimità del fondo tondeggiante di una scodella, una pallina fissata al centro di una corda di chitarra mantenuta tesa tra due estremi.

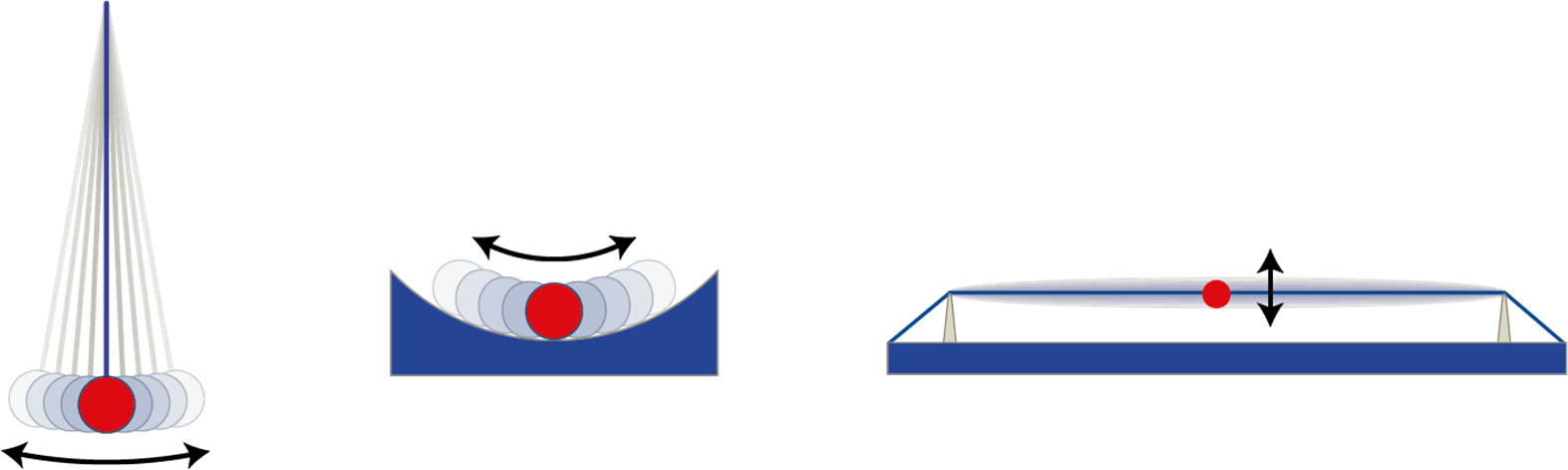
In tutti questi casi si ha un moto oscillatorio, che però non è necessariamente di tipo armonico (ad es. il pendolo semplice oscilla con moto armonico solo per piccole oscillazioni).

Tuttavia, se lo spostamento si mantiene sufficientemente piccolo, accade che la forza di richiamo è con ottima approssimazione proporzionale allo spostamento stesso. Pertanto, anche in tali casi (oltre che in quello paradigmatico massa-molla) si ha un moto armonico, purché l’ampiezza di oscillazione sia abbastanza piccola. Per quanto riguarda lo specifico caso del pendolo, questa proprietà era stata ben compresa da Galilei che quattro secoli fa mise in evidenza “l’isocronismo delle piccole oscillazioni”.

12. Ulteriori riflessioni sul moto armonico

Come ricordato nella sezione precedente, i sistemi che possono compiere un moto di tipo armonico sono molteplici e molto diversi tra loro. Tuttavia, proprio perché si tratta della stessa tipologia di moto, ci sono alcune caratteristiche cinematiche che li accomunano. La figura seguente ne illustra due, prendendo ancora una volta ad esempio il sistema massa-molla: l’indipendenza del periodo dall’ampiezza (isocronismo) e l’andamento della velocità del corpo durante le varie fasi dell’oscillazione.

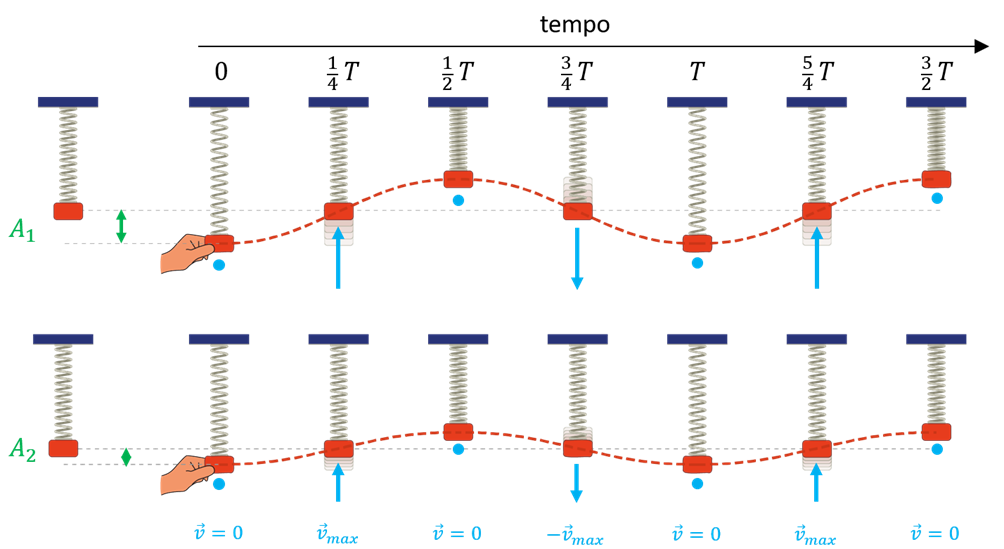
Per quanto riguarda il primo aspetto, con riferimento alla figura, le diverse fasi del moto (massima estensione, passaggio dalla posizione di equilibrio, massima compressione, nuovo passaggio posizione di equilibrio, massima estensione, ecc…) avvengono con gli stessi intervalli di tempo, indipendentemente da quanto la molla venga discostata inizialmente dall’equilibrio. Per quanto riguarda il secondo aspetto (sempre con riferimento alla figura), osserviamo che la massa oscillante risulta ferma alle “estremità” dell’oscillazione (cioè all’istante zero di massima estensione e ai successivi istanti multipli di mezzo periodo); mentre raggiunge il massimo modulo della velocità quando transita (in un verso o nell’altro) dalla posizione di equilibrio: a un quarto di periodo, a tre quarti, cinque quarti, ecc...

13. Parametri caratteristici

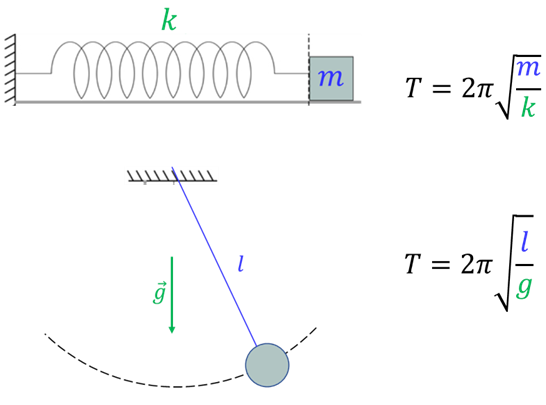
Concludiamo la nostra sintesi sul moto armonico ricordando che, come tutti i moti periodici, esso è caratterizzato anche dalla frequenza che, come abbiamo prima ricordato, è pari al reciproco del periodo. Per due dei principali tipi di oscillatori armonici (il sistema massa-molla e il pendolo semplice) la figura seguente riassume la dipendenza del periodo dai parametri caratteristici degli oscillatori: lunghezza l del filo e accelerazione di gravità g, per il pendolo; costante elastica k della molla e massa \( \textbf{m} \) del corpo attaccato, per il sistema massa-molla.

14. Onde

I fenomeni ondulatori, cioè quelli che coinvolgono la propagazione di una perturbazione di una determinata proprietà di un mezzo, sono numerosi. Ci sono esempi ben visibili: le onde su una corda fissata a un estremo, il cui altro estremo sia mosso ritmicamente su e giù; le onde che si propagano in uno specchio d’acqua dal punto in cui viene fatto cadere un sassolino; le onde del mare. E ci sono poi molti altri fenomeni ondulatori che non sono immediatamente riconoscibili come tali, dal momento che la perturbazione che si propaga non si vede direttamente: il suono (che consiste di onde meccaniche che si propagano in un mezzo materiale); le onde elettromagnetiche, con i diversi nomi assunti in base alle loro caratteristiche (onde radio, microonde, infrarosso, luce visibile, ecc.). Per queste ultime, ciò che si propaga è l’energia, sotto forma di campo elettromagnetico, una proprietà dello spazio-tempo stesso che, come tale, non necessita di un mezzo materiale per propagarsi. In generale va ricordato che in qualsiasi onda ciò che si propaga lungo la direzione di propagazione è l'energia; senza che ci sia trasporto di materia, la quale oscilla semplicemente attorno alla posizione di equilibrio.

15. I fenomeni ondulatori

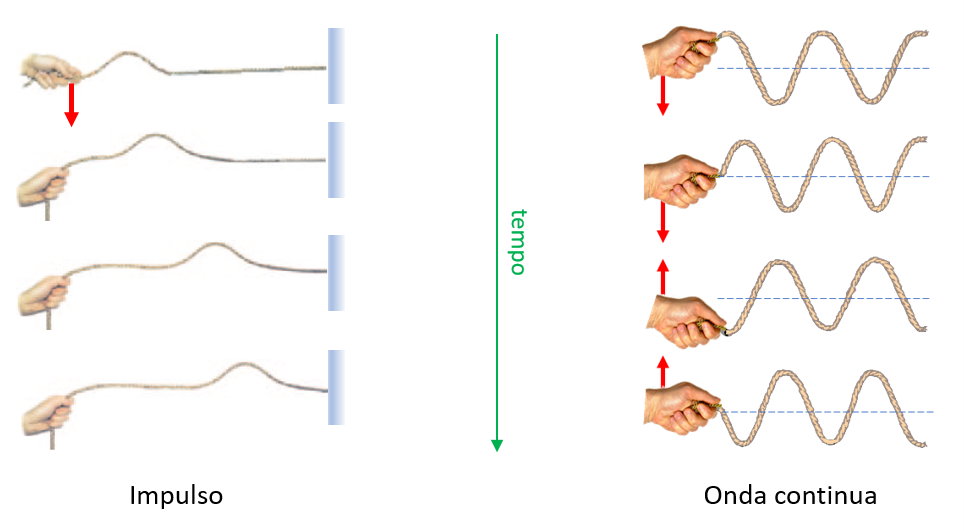
I fenomeni ondulatori possiamo distinguerli in impulsivi (una singola perturbazione che si propaga nello spazio, ma non si ripete nel tempo) e continui (la propagazione della perturbazione si ripete regolarmente anche nel tempo). Il termine onde è utilizzato generalmente per quest’ultima tipologia di fenomeni ondulatori.

La figura seguente mette a confronto la propagazione su una corda tesa: di un impulso (la mano imprime un solo strattone giù/su alla corda), e di un’onda continua (la mano continua a fare giù e su periodicamente).

16. Onde longitudinali e trasversali

Un’altra importante classificazione delle onde è tra longitudinali e trasversali. Questa distinzione è basata sulla relazione che c’è, in un dato tipo di onda, tra la direzione di propagazione e quella di oscillazione. In particolare, un’onda è di tipo longitudinale se oscilla nella stessa direzione in cui si propaga; è invece trasversale se l’oscillazione avviene in direzione perpendicolare rispetto a quella di propagazione. L’onda sulla corda illustrata nella figura precedente è di tipo trasversale. La figura seguente mette a confronto i due tipi di onda che possono instaurarsi su una lunga molla (di tipo Slinky) fissata a un estremo.

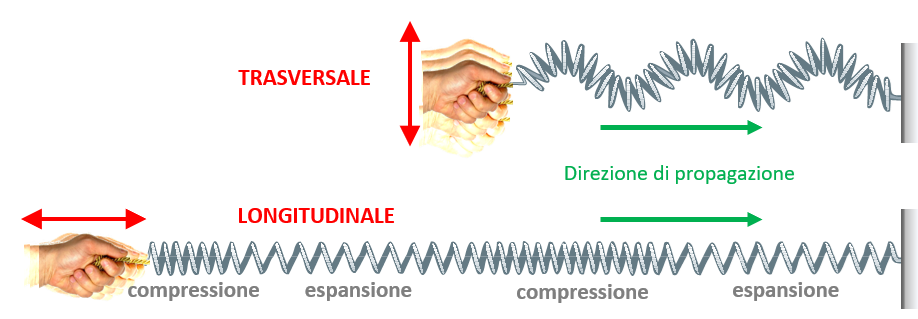
Se l’altro estremo viene forzato con la mano a muoversi su e giù, lungo la molla si propaga un’onda che somiglia a quella sulla corda (onda trasversale); se invece l’estremo della molla viene mosso ritmicamente avanti e indietro nella medesima direzione della molla, lungo di questa si propaga un’onda consistente in una successione di regioni in cui la molla è espansa o compressa (rispetto alla sua situazione di riposo).

17. Le onde (continue)

Le onde (continue) sono fenomeni caratterizzati da un duplice periodicità: nel tempo e nello spazio. Se ad esempio consideriamo la corda sulla quale si propaga un’onda trasversale e fissiamo l’attenzione su un determinato punto di essa, vedremo tale punto fare su e giù al passare del tempo, compiendo proprio un moto armonico: il periodo di tale moto è detto periodo (temporale) dell’onda e il suo reciproco è la frequenza: \( f=\frac1T \) . D’altra parte, se consideriamo il profilo dell’onda a un istante di tempo fissato, avremo una curva sinusoide, per la quale due picchi successivi ricorrono sempre alla stessa distanza l’uno dall’altro: tale distanza (cioè il “periodo spaziale” di ripetizione del profilo dell’onda a tempo fissato) è detta lunghezza d’onda ed è generalmente indicata col simbolo λ. Frequenza e lunghezza d’onda sono legate tra loro da una relazione molto importante: il loro prodotto è pari alla velocità di propagazione dell’onda: \( λf=v \).

18. Sistemi di riferimento non inerziali

Il primo principio della dinamica (principio d’inerzia) individua il moto rettilineo uniforme come stato di moto “naturale” di un corpo; cioè il tipo di moto eseguito da un corpo sul quale la risultante delle forze sia nulla. Esistono però dei sistemi di riferimento nei quali il principio d’inerzia non è valido: vengono perciò denominati “non inerziali”. Consideriamo il seguente esempio. Sei in un’automobile che si muove a velocità costante su una strada rettilinea di pianura; sul sedile vuoto del passeggero è posata un’arancia, la quale resta ferma. A un certo punto il guidatore, vedendo una mucca che si accinge ad attraversare la strada, frena con decisione, facendo diminuire la velocità dell’automobile. Cosa fa l’arancia? Da ferma che era si mette “spontaneamente” in moto e rotola fuori dal sedile (e d’altra parte anche tu, che sei seduta sul sedile posteriore, ti senti spinta in avanti). Pertanto nel sistema di riferimento solidale all’automobile in frenata il primo principio della dinamica è violato: infatti un oggetto da fermo si è messo in moto (cioè ha subito un’accelerazione) senza che su di esso si esercitassero forze.

Per individuare i sistemi di riferimento inerziali basta conoscerne uno: infatti, dato un sistema inerziale, tutti e soli quelli che si muovono rispetto a questo di moto rettilineo uniforme sono pure inerziali. Con ottima approssimazione, è inerziale un sistema di riferimento che si muove di moto rettilineo uniforme rispetto al Sole. Con approssimazione ancora migliore lo è uno che si muova di moto rettilineo uniforme rispetto alle stelle molto lontane (le cosiddette stelle fisse).

19. Forze apparenti

Nei sistemi di riferimento non inerziali il comportamento dei corpi in moto non segue le leggi di Newton. Tuttavia, poiché tali leggi sono molto comode e utili, spesso si ricorre a un “trucco” per ripristinarne la validità anche nei sistemi di riferimento non inerziali: si introducono in essi delle forze cosiddette “apparenti”. Queste sono così denominate per via del fatto che non sono forze effettivamente esercitate sul corpo in esame da un altro corpo. Ricordiamo infatti che le forze in senso proprio sono caratterizzate dalla terza legge della dinamica, e sono pertanto “inter-azioni”; cioè la forza agente su un corpo coinvolge sempre un altro corpo. Invece, ad esempio, nel caso prima esaminato dell’arancia sul sedile, questa si mette in moto “come se” una forza la spingesse in avanti durante la frenata, senza però che ci sia effettivamente un altro corpo che da essa venga “tirato” all’indietro (azione e reazione). Giocando un po’ con la seconda legge della dinamica è possibile dimostrare che questa ritorna a essere valida, per un corpo di massa m, anche in un sistema di riferimento non inerziale che abbia accelerazione \( \vec{a}_S \) rispetto a un sistema inerziale, pur di assumere che sul corpo agisca una forza \( \vec{F}_{app}=-m \vec{a}_S \), oltre alle eventuali forze effettive presenti.

20. Esempio

Pertanto, nell’automobile in frenata (caratterizzata quindi da una accelerazione avente verso opposto alla velocità) comparirà una forza apparente avente lo stesso verso della velocità, e che quindi “spinge” in avanti. Similmente, un’automobile che percorre una curva verso destra a velocità di modulo constante possiede un’accelerazione diretta trasversalmente all’auto verso destra, cioè verso il centro della curva (accelerazione centripeta); pertanto, nel sistema di riferimento solidale all’automobile compare una forza apparente diretta verso l’esterno della curva, che sarà responsabile del fatto che i passeggeri si sentono spinti contro la parete sinistra dell’automobile: tale spinta apparente è comunemente detta forza centrifuga. In realtà non c’è nessun agente fisico che spinga i passeggeri verso l’esterno della curva; ce n’è invece uno (la forza di attrito tra pneumatici e strada) che spinge l’automobile verso l’interno, costringendola a deviare dalla traiettoria rettilinea che altrimenti essa seguirebbe obbedendo al principio d’inerzia. In effetti i passeggeri rispetto all’auto si sentono spinti apparentemente verso sinistra perché essi, obbedendo al principio di inerzia, tenderebbero a continuare a muoversi in linea retta rispetto al suolo.

21. Specificità dei sistemi di riferimento rotanti

Una tipologia di sistemi non inerziali di particolare importanza (sia pratica che concettuale) è costituita da quelli che sono in rotazione rispetto a un sistema di riferimento inerziale. Ad esempio il piano di una giostra; ma anche la Terra in relazione al suo moto di rotazione attorno al proprio asse. In tali sistemi, oltre alla già citata forza apparente centrifuga (che, ricordiamo, è diretta in verso opposto all’accelerazione del sistema rotante, che è centripeta) compare un’ulteriore forza apparente, la forza di Coriolis, dipendente dalla velocità (che quindi non si manifesta sui corpi fermi nel sistema rotante), il cui effetto è quello di provocare una deviazione del moto dei corpi in direzione costantemente perpendicolare alla velocità. Questo fa sì che un corpo in moto in un sistema rotante tenda a percorrere una traiettoria di tipo spiraleggiante. Questo fenomeno è di estrema importanza in meteorologia e nello studio dei moti dell’atmosfera, in quanto è alla base della formazione delle aree cosiddette cicloniche. Si tratta di porzioni di atmosfera in cui la pressione è inferiore a quella delle zone circostanti e in corrispondenza delle quali si instaurano moti vorticosi che portano a una rotazione complessiva in senso antiorario, nell’emisfero boreale, mentre la rotazione è in senso orario in quello australe.

La forza apparente di Coriolis si manifesta in maniera spettacolare nel comportamento del pendolo di Foucault, il quale ideò e realizzò il famoso esperimento proprio per evidenziare la rotazione terrestre attraverso la non inerzialità da essa derivante.