Il fissaidee
| Sito: | Federica Web Learning - LMS |
| Corso: | Scienze fisiche di base |
| Unit: | Il fissaidee |
| Stampato da: | Utente ospite |
| Data: | martedì, 26 agosto 2025, 20:24 |
1. Fluidi incomprimibili e loro descrizione

Quinta tappa
Il termine “Fluidi” indica collettivamente i due stati di aggregazione della materia nei quali essa è in grado di scorrere, cioè - appunto - di “fluire”. Fluidi sono, quindi, i liquidi e i gas. Dal punto di vista linguistico è utile prestare attenzione al fatto che nel parlare comune, a differenza di quanto avviene col linguaggio della fisica, il termine “fluido” spesso viene inteso come sinonimo di “liquido”!
Caratteristica comune dei fluidi è la mancanza di una forma propria. Ad esempio, l’acqua contenuta in un bicchiere ha una forma approssimativamente cilindrica; se però la stessa acqua viene versata per terra, assumerà la forma di uno strato sottile. Stesso discorso per i gas: del fumo contenuto in un palloncino posto in una scatola sigillata ha una forma grosso modo sferica; se però il fumo viene lasciato uscire dal palloncino assumerà essenzialmente la forma della scatola. Cos’è dunque che differenzia i liquidi dai gas, dal momento che entrambi sono privi di forma propria? È il comportamento del loro volume. Infatti, una porzione di liquido possiede un volume fissato: ad esempio l’acqua contenuta in una bottiglia da un litro, continuerà ad avere il volume di un litro anche se la versiamo sul pavimento. Mentre una porzione di gas assume immancabilmente il volume massimo possibile, compatibilmente col contenitore nel quale è eventualmente confinata. Riprendendo l’esempio del palloncino pieno di fumo citato sopra, quando il fumo è costretto nel palloncino ha un certo volume; invece quando viene lasciato uscire da esso finirà con l’occupare l’intera scatola, assumendo quindi un volume maggiore.
La proprietà di un materiale, consistente nel mantenere invariato il volume di una fissata porzione di esso, è detta incomprimibilità. Pertanto i fluidi incomprimibili sono essenzialmente quelli che chiamiamo liquidi. Il concetto di incomprimibilità lo abbiamo sin qui descritto a parole, cioè qualitativamente. Come ben sappiamo, però, per poter fare scienza è necessario esprimere le proprietà fisiche mediante grandezze suscettibili di essere misurate. La grandezza che permette di definire in maniera quantitativa l’incomprimibilità di un materiale è la sua densità. Questa, generalmente indicata con la lettera greca \( \rho \), è definita come il rapporto tra la massa \( M \) di una data porzione del materiale e il volume \( V \) che questa occupa: \( ρ=M/V \). Pertanto nel S.I. la sua unità di misura è kg/m3.
Possiamo quindi dire che un fluido incomprimibile ha densità costante (a una fissata temperatura). Così, per esempio, la densità dell’acqua è circa uguale a 103 kg/m3 (a temperatura ambiente) e non dipende dal fatto che l’acqua sia posta in un bicchiere aperto oppure la si tenga “pressata” in una siringa tappata dalla parte dell’ago. La densità dell’aria che respiriamo, a sua volta, è pari a circa 1,23 kg/m3 in condizioni standard. Tuttavia, se riempiamo d’aria una siringa tappata dal lato dell’ago e spingiamo sullo stantuffo, riusciamo ad aumentare con grande facilità la densità dell’aria in essa contenuta, come risulta evidente dal fatto che il suo volume diminuisce, mentre la massa resta costante.
Per spostarti tra le pagine del fissaidee utilizza le frecce azzurre.
2. La pressione nei fluidi incomprimibili

Consideriamo un recipiente cilindrico pieno d’acqua (parte sinistra della figura). Se pratichiamo dei forellini a diverse profondità sotto il pelo dell’acqua, da ciascuno di essi sprizza il liquido: si può facilmente verificare sperimentalmente (ad esempio facendo l’esperimento con una bottiglia di plastica) che la velocità con cui l’acqua sprizza è tanto maggiore quanto più in profondità è il corrispondente forellino. Ad esempio, nel caso rappresentato in figura, l’acqua sprizza da C più velocemente che da B, da cui sprizza a sua volta più velocemente che da A. Questo fatto ci suggerisce che più il forellino è in basso, maggiore è la forza che agisce dall’interno sull’acqua in prossimità del forellino, spingendola fuori. Ma di che forza si tratta? È la forza esercitata dall’acqua sovrastante il forellino a causa del suo peso (e del fatto che, a sua volta, sulla superficie libera dell’acqua nel contenitore preme l’atmosfera). Naturalmente la presenza di questa forza che preme dall’interno è indipendente dal fatto che ci sia o meno il forellino. Pertanto, considerando una superficina S della parete (parte destra della figura) possiamo concludere che su di essa agisce una forza, perpendicolare alla parete stessa; come vedremo fra poco, l’intensità di questa forza dipende dalla profondità. Ciò che è realmente importante per descrivere e spiegare il comportamento dell’acqua che sprizza, non è tanto l’intensità della forza che spinge da dentro perpendicolarmente alla superficie, quanto il rapporto tra tale intensità e l’area della superficie stessa. Questo rapporto prende il nome di pressione e di norma si indica con il simbolo P:
\( \textbf{P=F/S} \)
Da questa definizione segue che l’unità di misura della pressione (denominata Pascal, simbolo Pa) è pari al rapporto tra quella della forza (N) e quella della superficie (m2):
\( \textbf{Pa=N/m}^{2} \)
3. La pressione atmosferica
L’aria atmosferica, per quanto impalpabile, esercita una notevole pressione su tutte le superfici esposte a essa. Questo fatto può essere verificato in diversi modi, alcuni dei quali decisamente affascinanti, come ad esempio lo storico esperimento degli emisferi di Magdeburgo, condotto a metà Seicento (puoi trovarne la descrizione su questa pagina web).
Tra i diversi esperimenti volti a evidenziare la pressione atmosferica, un rilievo particolare è rivestito da quello condotto dall’italiano Evangelista Torricelli nel 1643. Infatti col suo celebre esperimento Torricelli, oltre a dimostrare che l’atmosfera esercita una pressione, ne determinò quantitativamente l’intensità, mediante confronto con la pressione esercitata da un liquido noto: il mercurio.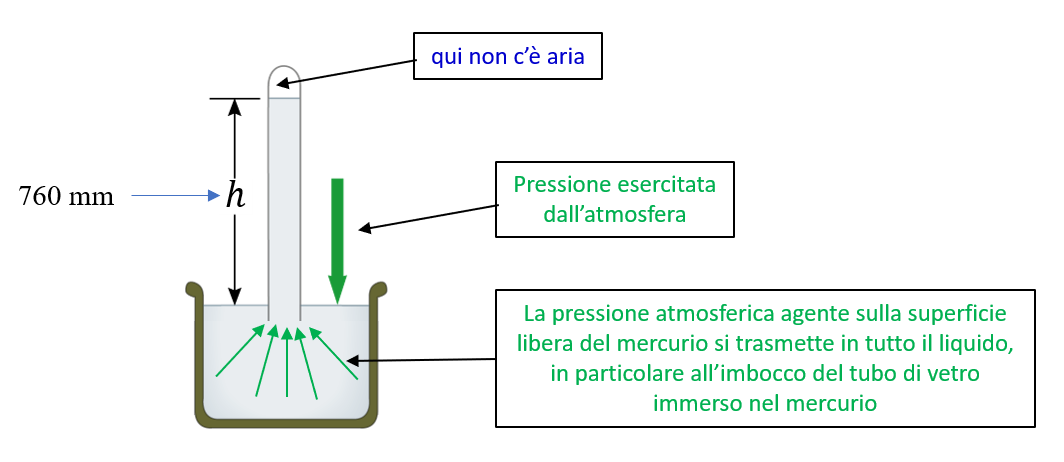
L’esperimento di Torricelli è schematizzato in figura. Un tubo di vetro aperto a un estremo viene riempito completamente di mercurio e capovolto in una bacinella contenente a sua volta mercurio. In queste condizioni si osserva che il tubo si svuota parzialmente nella bacinella, fino a che il livello del mercurio in esso si porta al valore di 76 cm rispetto al pelo libero del liquido nella bacinella. Per comprendere come si instaura questa condizione di equilibrio, consideriamo uno straterello di mercurio nel tubo situato alla stessa quota della superficie di quello nella bacinella. Questo straterello sarà sottoposto: alla pressione dovuta alla colonna di 76 cm di mercurio sovrastante (che preme verso il basso) e a quella atmosferica che preme verso l’alto attraverso il mercurio nella bacinella (grazie al principio di Pascal che ci assicura che la pressione atmosferica esercitata sulla superficie libera del liquido si trasmette uguale ovunque). Da questo si deduce che la pressione atmosferica equivale a quella esercitata da una colonna di mercurio alta 76 cm = 760 mm. Il risultato di questo esperimento ha portato storicamente all’introduzione di un’unità di misura della pressione (non facente parte del S.I.) dal nome eloquente: il “millimetro di mercurio”, simbolo mmHg, detto anche torr. Per definizione 1 torr = (1/760) atm; dove quest’ultima unità di misura, l’atmosfera, ormai poco utilizzata, è definita come il valore della pressione atmosferica in condizioni standard (a livello del mare, a 0°C, a 45° di latitudine e in particolari condizioni di umidità). Vedremo più avanti come sia possibile determinare il fattore di conversione tra il mmHg e il Pa.
4. Il principio di Pascal
Un aspetto molto importante del comportamento della pressione in un fluido in quiete è stato riconosciuto, e formulato sotto forma di principio fisico nel Seicento, dall’eclettico filosofo/fisico/matematico francese Blaise Pascal. Lo stesso al quale è stata intitolata l’unità di misura S.I. della pressione.
Il principio di Pascal afferma che: una variazione di pressione applicata a un liquido in quiete chiuso in un contenitore si trasmette egualmente a ogni porzione del liquido, nonché alle pareti del contenitore che sono in contatto col liquido stesso. La validità di questo principio può essere verificata sperimentalmente in vari modi, ad esempio come illustrato nella figura.

Il principio di Pascal lo si può trovare “in azione” in moltissimi contesti differenti. Il più noto, riportato praticamente in tutti i libri di testo (e pertanto non lo richiamiamo qui, invitandoti a consultare il tuo testo), è quello del martinetto idraulico. Si tratta di un dispositivo utilizzato, ad esempio, per sollevare un’automobile di massa dell’ordine dei 1000 kg, utilizzando una forza corrispondente al peso di poche decine di kg.
Meno evidente è il ruolo del principio di Pascal nel meccanismo della circolazione sanguigna. Infatti, ogni volta che il cuore si contrae (tipicamente un po’ più di una volta al secondo) spinge il sangue nell’aorta, a causa dell’aumento di pressione che la contrazione provoca nel cuore stesso (in maniera analoga a quando strizziamo tra le mani un palloncino pieno d’acqua). Tale aumento di pressione, in accordo con il principio di Pascal, si trasmette attraverso le arterie del corpo. Similmente, durante la fase di rilassamento del cuore tra una contrazione e l’altra, si ha una riduzione della pressione nelle cavità cardiache, e anche questa si trasmette in tutte le arterie. Di conseguenza, in un qualunque punto lungo il percorso arterioso la pressione varierà in funzione del tempo con un andamento simile a quello mostrato in figura.
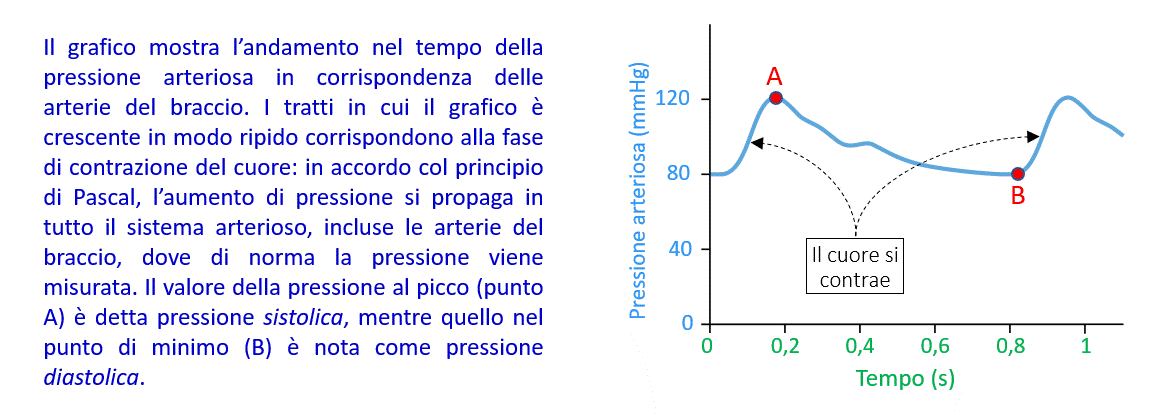
Osserviamo che l’unità di misura usualmente impiegata per esprimere la pressione arteriosa è il mmHg, che come ricorderai abbiamo introdotto in relazione all’esperimento di Torricelli.
5. La legge di Stevin /1
Un liquido in quiete in un contenitore esercita una pressione su ogni punto delle pareti (e, più in generale, di qualunque superficie con la quale sia in contatto – ad esempio quella di un corpo immerso in esso) che risulta tanto più intensa quanto maggiore è la profondità del punto considerato. Nell’esempio riportato in figura la pressione nel punto 3 è maggiore di quella nel punto 2, che a sua volta è maggiore della pressione in 1. La relazione quantitativa tra la pressione in un punto e la sua profondità sotto la superficie del liquido è espressa dalla legge di Stevin:\( P=ρgh \)
dove \( ρ \) è la densità del liquido, \( g \) l’accelerazione di gravità e \( h \) la profondità del punto (vedere esempi in figura).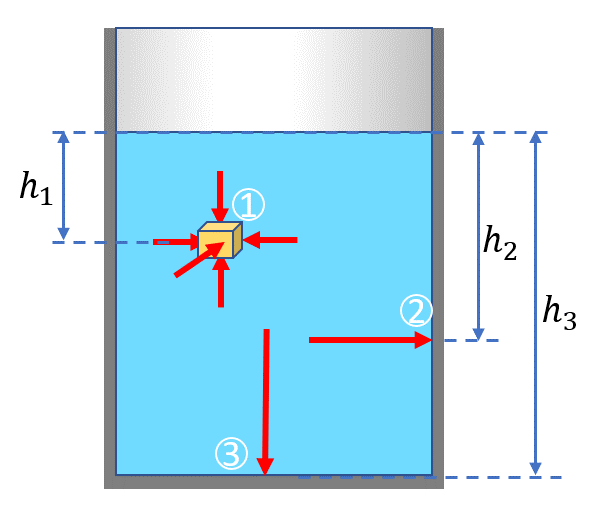
ATTENZIONE: un errore comune è di interpretare \( h \) nella legge di Stevin come l’altezza del punto rispetto al fondo del contenitore, anziché la sua profondità rispetto alla superficie libera del liquido.
Osserviamo che se il contenitore è aperto, o comunque la superficie del liquido è in contatto con l’aria atmosferica, su tale superficie agirà la pressione atmosferica. Di conseguenza, per il principio di Pascal, tale extra-pressione si trasmetterà in ogni punto del liquido. Pertanto la forma più generale della legge di Stevin è\( P=P_{atm}+ρgh \)
dove il primo addendo a secondo membro indica la pressione atmosferica agente sulla superficie libera del liquido.6. La legge di Stevin /2
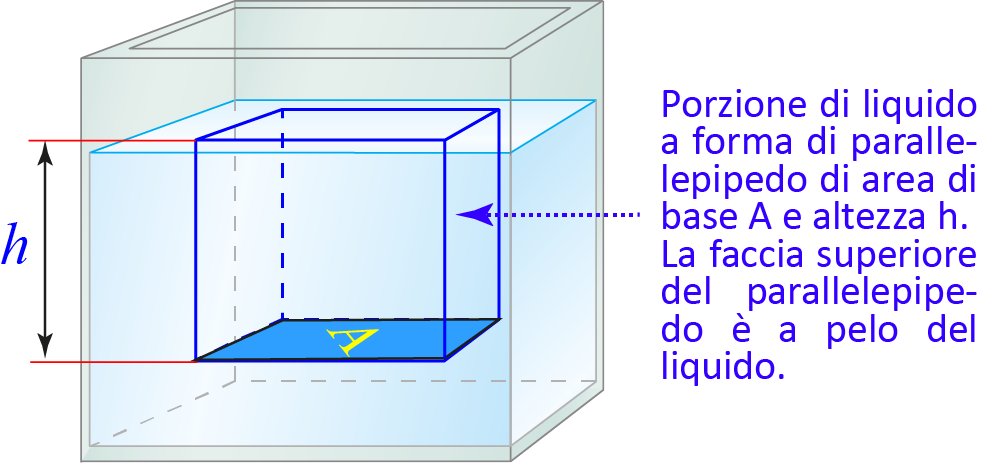
\( m=Vρ=Ahρ \)
Utilizzando ora la definizione di pressione e sostituendo le espressioni trovate, si ha: \( P=F_p/A=Ahρg/A=ρgh \) che è la legge di Stevin. Come chiarito prima, questo è il contributo alla pressione dovuto al solo liquido nel recipiente; a questo occorrerà eventualmente sommare la pressione atmosferica, se quest’ultima agisce sulla superficie del liquido.La legge di Stevin può essere utilizzata per determinare il fattore di conversione tra l’unità di misura S.I. della pressione (il Pascal) e l’unità pratica introdotta in connessione con l’esperimento di Torricelli (il millimetro di mercurio, mmHg, o torr). A tal fine consideriamo un tubo riempito di mercurio fino a un’altezza \( h \)=76 cm come nell’esperimento (ricordiamo che il tubo in questione è chiuso in alto, e sulla superficie del mercurio non agisce la pressione atmosferica, che invece agisce dal basso impedendo al mercurio di uscire nella bacinella). Uguagliando la pressione atmosferica a quella esercitata dalla colonna di mercurio alla base (ottenuta dalla legge di Stevin) si ha:
\( 1 atm= ρ_{Hg} gh \)
Dove \( ρ_{Hg}=1{,}355×10^4 \, kg/m^3 \) è la densità del mercurio.
Sostituendo i valori numerici \( g=9{,}81 m/s^2 \) e \( h=0{,}76 m \) si ottiene \( 1 atm=1{,}01×10^5\, Pa \) .
Questa relazione indica che l’unità di misura Pascal è molto piccola rispetto ai valori con cui abbiamo a che fare nella vita quotidiana, che sono tipicamente dell’ordine dell’atmosfera.
7. Legge di Archimede e galleggiamento
Il galleggiamento di un corpo (o l’affondamento, più o meno rapido) è uno dei fenomeni connessi ai liquidi maggiormente noto e facilmente osservabile. Ed è altrettanto noto che la legge empirica che governa il comportamento di un corpo (galleggiamento o affondamento) è stata individuata da Archimede intorno al 3° secolo a.C. Non richiameremo qui il notissimo episodio che ha per protagonista la corona di presunto oro del tiranno di Siracusa, Gerone. Tuttavia è opportuno ricordare un aspetto di questo episodio aneddotico: Archimede ebbe l’illuminazione (Eureka!) che lo condusse a risolvere il quesito postogli da Gerone (la corona è tutta d’oro, oppure no?) allorché immergendosi nella vasca da bagno percepì di sentirsi più leggero. Poiché il suo peso non poteva essere cambiato (come dimostrato dalla constatazione che uscito dall’acqua ritornava a percepire il suo peso normale) concluse che era l’acqua a esercitare sul suo corpo un’azione (noi oggi utilizziamo il termine “forza”) che contrasta il peso, e quindi diretta verso l’alto.
Il principio formulato da Archimede, espresso in linguaggio moderno, afferma che allorché un corpo è immerso (totalmente o parzialmente) in un liquido, quest’ultimo esercita sul corpo una forza diretta verso l’alto di intensità pari al peso del liquido spostato dalla parte immersa del corpo (eventualmente tutto). È chiaro quindi che il comportamento del corpo (galleggia o affonda?) dipende dal confronto tra l’intensità della sua forza peso, \( F_p \) , e quella della forza
esercitata dal liquido, \( F_A \) (che chiameremo forza di Archimede o, più
propriamente, forza idrostatica). È opportuno ricordare che in relazione al
principio di Archimede spesso viene utilizzato il termine “spinta” come
sinonimo di forza.
Alla luce di quanto detto,
il corpo sprofonda se \( F_p>F_A^{max} \)dove \( F_A^{max} \) indica il massimo valore che può assumere la
forza idrostatica, corrispondente a quando il corpo è completamente immerso e
quindi il volume di liquido spostato è il massimo possibile. In caso contrario
il corpo galleggia, emergendo più o meno dal liquido.

8. La condizione di affondamento /1
La condizione di affondamento (e quindi quella, reciproca, di galleggiamento) può essere espressa in una forma immediatamente utilizzabile per prevedere il comportamento di un corpo in un determinato liquido. Vediamo come.
La forza peso agente sul corpo è \( F_p=mg=Vρ_c g, \) dove \( V \)è il volume del corpo e \( ρ_c \) la sua densità. D’altra parte, esaminando con attenzione l’enunciato del principio di Archimede possiamo esprimere la forza idrostatica come \( F_A^{max}=m_L g=V_{imm} ρ_L g=V ρ_L g \), dove \( m_L \) indica la massa del liquido
spostato dal corpo, \( V \) il volume del corpo, \( V_{imm} \) la porzione di volume che
risulta immersa (la quale, nel caso considerato è uguale all’intero volume \( V \)) e \( ρ_L \) è la densità del liquido.
Sostituendo le espressioni delle forze nella condizione di affondamento \( F_p>F_A^{max} \) e semplificando membro a
membro \( V \) e \( g \) la condizione per
l’affondamento diventa: \( ρ_c>ρ_L \). Abbiamo quindi un criterio per prevedere se un corpo posto in un liquido galleggerà (se la sua densità è inferiore a quella del liquido) oppure affonderà (nel caso contrario). Come si comporta il corpo se la sua densità è proprio uguale a quella del liquido? Si troverà in una condizione particolare, detta di galleggiabilità neutra, nella quale resterà sospeso nel liquido alla profondità alla quale viene collocato da fermo, senza andare né su né giù! Questo fenomeno è utilizzato dai pesci per restare fermi a “mezz’acqua” senza dover utilizzare le pinne per spingersi in su o in giù. I pesci, infatti, sono dotati di un sacchetto nell’addome, detto vescica natatoria, che possono gonfiare e sgonfiare per variare la densità media del loro corpo.
9. La condizione di affondamento /2
Per determinare la
condizione di affondamento abbiamo considerato il caso in cui il corpo è totalmente
immerso nel liquido e quindi \( V_{imm}=V \). Tuttavia, nel regime di
galleggiamento, cioè quando \( ρ_c<ρ_L \), il corpo è solo
parzialmente immerso. In tal caso è utile chiedersi quale sia la frazione del
volume del corpo che risulta immersa, cioè il valore del rapporto \( V_{imm}/V \) Possiamo determinarla
considerando le grandezze illustrate nella figura.
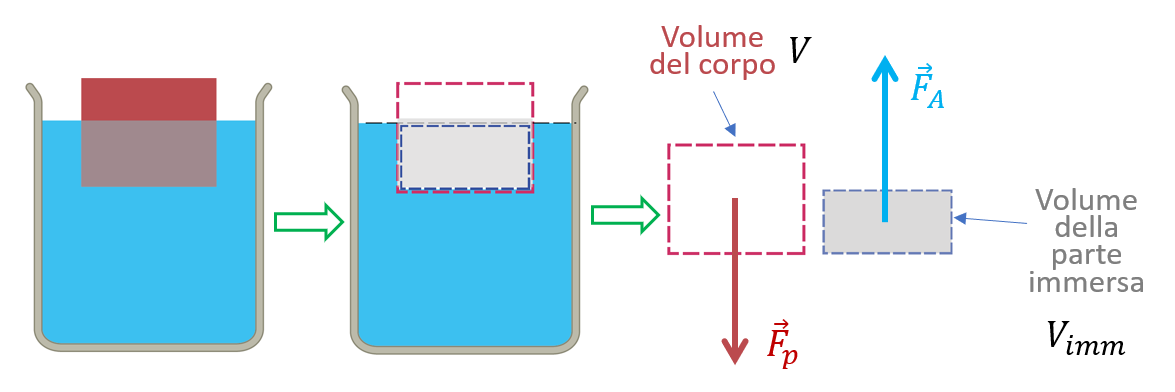
In questo caso la condizione di equilibrio \( F_p=F_A \)si esprime come \( ρ_c g=V_{imm} ρ_L g \)Da qui, semplificando l’accelerazione di gravità otteniamo \( V_{imm}/V=ρ_c/ρ_L \). Quindi la frazione di volume del corpo che risulta immersa è pari al rapporto tra la densità del corpo e quella del liquido. Questo fatto è particolarmente significativo nel caso in cui il corpo è costituito di ghiaccio e il liquido è l’acqua. Conosci il modo di dire “… è solo la punta dell’iceberg"? Per intendere che ciò che appare è solo una minima parte della realtà intera? Ebbene, vedremo ora l’origine fisica di questo modo di dire chiedendoci qual è la frazione del volume di un iceberg che emerge dall’acqua. La risposta la possiamo ottenere ricordando che la densità del ghiaccio è \( ρ_c=0{,}92 g/cm^3, \) mentre quella dell’acqua è \( ρ_L=1 g/cm^3 \). Sostituendo tali valori nella formula ricavata prima otteniamo\( V_{imm}/V=0{,}92 \). In termini percentuali questo significa che il 92% dell’iceberg è immerso e quindi la parte che si vede è solo l’8% circa! In realtà il conto che abbiamo fatto sottostima un po’ la percentuale emersa, in quanto non abbiamo tenuto conto che l’iceberg è fatto di acqua dolce, mentre l’acqua in cui galleggia è salata. Poiché quest’ultima ha una densità un po’ maggiore di \( 1 g/cm^3 \) (dipende dal mare considerato, ma mediamente è \( ρ_L=1{,}02 g/cm^3 \) si ottiene una percentuale emersa intorno al 10%; in ogni caso questo non inficia il modo di dire!