Il fissaidee
| Sito: | Federica Web Learning - LMS |
| Corso: | Scienze fisiche di base |
| Unit: | Il fissaidee |
| Stampato da: | Utente ospite |
| Data: | martedì, 26 agosto 2025, 20:24 |
Indice Unit
- 1. La temperatura
- 2. Equilibrio e “Principio Zero” della termodinamica
- 3. Termometri e scale di temperatura
- 4. Non tutti i corpi si scaldano allo stesso modo: il calore specifico
- 5. Dal calorico al calore come energia trasportata microscopicamente
- 6. L’energia interna e il Primo Principio della termodinamica.
- 7. Dagli scaldamuscoli ai motori: il Secondo Principio
- 8. L’entropia e la freccia del tempo
- 9. Perché la termodinamica funziona: l’approccio statistico
- 10. Gas ideali e temperatura assoluta
- 11. L’equazione di stato dei gas ideali
- 12. Trasformazioni termodinamiche nei gas ideali
- 13. Cicli termodinamici, macchine termiche e frigoriferi
- 14. La “macchina ideale”: il ciclo di Carnot
- 15. Un tuffo nel mondo microscopico: la teoria cinetica dei gas
1. La temperatura

Sesta tappa
Oggetto della termodinamica è lo studio di sistemi macroscopici, che in pratica significa di tutte cose che cadono sotto i nostri occhi nella realtà quotidiana, come un libro, un bicchiere di latte, o noi stessi. Per descrivere questi sistemi sono necessarie delle nuove quantità fisiche che non sono grandezze puramente meccaniche, ma piuttosto “emergono” come proprietà collettive di oggetti formati da un grandissimo numero di atomi, ossia proprietà che non si possono attribuire a questa o quella particella che costituisce il sistema, ma solo al sistema nel suo complesso.
Il primo di questi personaggi è la temperatura.
Tutti abbiamo un’idea intuitiva dei concetti di “caldo” e “freddo”, ma i sensi ci possono ingannare. Ad esempio, se lasciamo per lungo tempo nel frigorifero due cubetti, uno di metallo e l’altro di polistirolo, molto probabilmente non ci sembrerà che siano alla stessa temperatura, ma effettivamente è così (poi capiremo perché).
Per capire davvero che cosa si intenda per “temperatura di un corpo”, e soprattutto come si possa quantificarne il valore, dobbiamo introdurre un concetto fondamentale, quello di equilibrio.
Per spostarti tra le pagine del fissaidee utilizza le frecce azzurre.2. Equilibrio e “Principio Zero” della termodinamica
L’esperienza quotidiana mostra come due sistemi fisici posti a contatto raggiungano uno stato di mutuo equilibrio, ossia una condizione in cui tutte le grandezze fisiche macroscopiche che li caratterizzano non cambiano più nel tempo.
Supponiamo ad esempio di scaldare con una fiamma una pallina metallica e di gettarla poi in un bicchiere d’acqua a temperatura ambiente. Dapprima l’acqua si agiterà, magari in parte bollirà se la pallina è davvero incandescente. Ma dopo un po’… calma piatta! L’acqua smetterà di agitarsi e, se toccata con un dito, la pallina non ci sembrerà né più calda né più fredda dell’acqua nel bicchiere.
L’equilibrio tra corpi ha una proprietà molto interessante: se un corpo A è in equilibrio con un corpo B, e il corpo B è in equilibrio con il corpo C, allora il corpo anche il corpo C è in equilibrio con il corpo A, cosa che ci permette di dividere tutti i corpi in “classi” costituite da tutti e soli quei corpi che sono in equilibrio tra di loro.
Questo “Principio Zero” della termodinamica può sembrare banale, ma in realtà è proprio quello che ci permette di introdurre la temperatura, come quella nuova grandezza fisica che ha lo stesso valore per tutti i corpi che si trovino in equilibrio tra di loro.
3. Termometri e scale di temperatura
Ma in che modo quantifichiamo questa misteriosa grandezza, la temperatura, che abbiamo appena introdotto? Ancora una volta ci viene in aiuto il Principio Zero: basta scegliere come “corpo C” un corpo per il quale assumiamo che una certa grandezza fisica vari con la temperatura secondo una legge precisa, magari linearmente come ragionevolmente si può ritenere (se la pressione non cambia) per il volume di una certa massa di gas, o per la lunghezza di una colonnina di mercurio contenuta in un tubicino di vetro graduato. Questo corpo C di “calibrazione” è ciò che diremo un termometro.
Per dare una misura della temperatura ci serve poi una scala, cosa che si può fare stabilendo che la proprietà che utilizziamo nel nostro termometro abbia un certo valore quando il termometro viene messo a contatto con un sistema in due condizioni termiche ben definite.
Ad esempio, potremmo mettere il nostro termometro a mercurio a contatto prima con una miscela di acqua e ghiaccio e poi con dell’acqua che bolle, e stabilire che queste condizioni corrispondono rispettivamente a 0 e 100 gradi “centigradi”, che indicheremo con “°C”. Questa è la scala Celsius, la principale (ma non l’unica) scala “empirica” di temperatura.
Vedremo poi come sia possibile introdurre una scala assoluta di temperatura, la scala Kelvin, che non sia legata a scelte pratiche ma un po’ arbitrarie come quella che abbiamo appena fatto: per ora anticipiamo che l’unità di questa scala, il kelvin (che si indica con “K”, senza il simbolo di grado) è uguale al grado centigrado, ma lo zero della scala è posto a -273.15°C (vedremo in seguito il perché).
4. Non tutti i corpi si scaldano allo stesso modo: il calore specifico
Per raggiungere la stessa temperatura due corpi posti a contatto devono potersi scambiare qualcosa, per quanto magari non si osservi alcun effetto meccanico: chiameremo questo “qualcosa” calore.
Anche se non sappiamo ancora che cosa veramente sia, qualche semplice esperimento come quello dell’irraggiamento di due cubetti che abbiamo visto nel filmato ci fa capire che il calore necessario per far variare di \( ΔT \) la temperatura di un corpo di massa \( m \) è diversa a seconda del materiale considerato. Possiamo infatti scrivere:
\( Q=c mΔT \)
dove \( c \), detto calore specifico del materiale, è la quantità di calore necessaria per innalzare di un grado una massa unitaria del materiale considerato.
L’unità di misura di \( c \) dipenderà naturalmente da quella con cui misuriamo il calore: per ora, misuriamolo con una nuova unità che diremo caloria (“cal”). Così facendo, nel Sistema Internazionale \( c \) si misura in cal/(kg°C), anche se è più frequente usare i grammi come unità di massa, perché in queste unità il calore specifico dell’acqua a temperatura ambiente è proprio pari a 1 cal/(g°C).
Mentre nel caso di solidi e liquidi non c’è sostanzialmente alcun problema a parlare di “un” calore specifico, nel caso dei gas le cose cambiano notevolmente, come vedremo, a seconda delle condizioni in cui lo misuriamo, per esempio tenendo costante il volume o la pressione del gas.
Il prodotto del calore specifico per la massa del corpo è detto capacità termica. È importante non confondere la capacità termica, che esprime di quanto calore ha bisogno un certo corpo per riscaldarsi, con la conducibilità termica, che invece esprime quanto in fretta un corpo può ricevere o fornire calore. È per la sua maggiore conducibilità termica che un cubetto di metallo estratto dal frigorifero sembra più freddo di uno di polistirolo di ugual massa (semplicemente perché vi raffredda più in fretta la mano!)
5. Dal calorico al calore come energia trasportata microscopicamente
Che cos’è davvero questo calore? Potrebbe essere una specie di “fluido”, una sostanza invisibile che passa da un corpo all’altro, quando vengano messi a contatto, fino a bilanciarne le temperature. Questo è di fatto ciò che pensavano i pionieri della termodinamica fino alla metà del XIX secolo, che chiamavano questo misterioso fluido “calorico”.
Ma c’è un grosso problema: la quantità di un fluido “materiale” non cambia (perché in fisica la massa si conserva), mentre è possibile far comparire del “calorico” letteralmente dal nulla. Provate infatti a sfregare vigorosamente la mano su una superficie, magari un po’ rugosa: vedrete che sia la mano che la superficie si scaldano. Perché? In realtà, per effetto dell’attrito tra la vostra mano e la superficie, avete “dissipato” il lavoro fatto per muovere la mano stessa. Quindi avete perso dell’energia meccanica, “creando” però del calore.
Che allora il calore non si altro che una forma di energia che, a differenza del lavoro meccanico, si trasporta “invisibilmente”, per via microscopica? Questa è la prima idea chiave che ha aperto le porte agli sviluppi della termodinamica. Come avete visto, James Prescott Joule riuscì proprio a stabilire un equivalente meccanico del calore, mostrando che:
\( 1 \textbf{cal} =4{,}186\, \textbf{J} \)
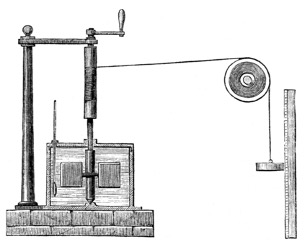
Il mulinello di Joule
6. L’energia interna e il Primo Principio della termodinamica.
Studiando la meccanica, abbiamo visto che, in presenza di quelle che abbiamo chiamato “forze conservative”, l’energia meccanica totale, somma dell’energia cinetica e di quella potenziale, si conserva. Possiamo pensare di generalizzare questa legge fondamentale introducendo in primo luogo il concetto di energia interna \( U \) di un corpo, che quantifica il suo “contenuto di energia” (come vedremo, \( U \) ha in effetti a che fare con l’energia meccanica delle molecole che lo compongono).
Da quanto abbiamo visto possiamo quindi supporre che l’energia interna di un corpo possa cambiare in soli due modi:
- perché sul corpo viene fatto del lavoro meccanico \( W \);
- perché al corpo viene trasferita energia in modo “invisibile” fornendogli del calore \( Q \).
Ossia, per la variazione \( \Delta U \) dell’energia interna scriveremo
\( \Delta U=W+Q \)
Dove, per quanto detto, scegliamo \( W>0 \) quando il lavoro è fatto sul (e non dal) corpo e \( Q>0 \) quando il calore è trasferito dall’esterno al corpo (e non viceversa). Quello che abbiamo annunciato è il Primo Principio della termodinamica: se volete, può essere anche visto come una definizione del concetto di calore che permetta di estendere il principio di conservazione dell’energia.
7. Dagli scaldamuscoli ai motori: il Secondo Principio
Il Secondo Principio della termodinamica esprime un concetto molto semplice e che è sicuramente in accordo con la nostra esperienza quotidiana: si può scaldare un corpo mettendolo a contatto con un corpo più caldo, ma non viceversa! Per essere più precisi, dovremmo dire, come disse Rudolf Clausius attorno a metà dell’800, che
“È impossibile realizzare una trasformazione termodinamica il cui unico risultato sia quello di far passare del calore da una sorgente a temperatura inferiore a una a temperatura superiore”
dove la specificazione “unico” è essenziale, altrimenti il Secondo Principio sarebbe banalmente violato da un condizionatore, che d’estate raffredda una stanza trasferendo calore all’ambiente esterno, decisamente più caldo: ma per farlo consuma un bel po’ di energia elettrica!
William Thompson (Lord Kelvin) diede un’interpretazione apparentemente molto diversa, ma in realtà equivalente, del Secondo Principio, affermando che
“È impossibile costruire una macchina che, operando ciclicamente, trasformi il tutto il calore assorbito da una singola sorgente in lavoro”.
Ad esempio, parte del calore prodotto dalla combustione della benzina in un motore a scoppio, viene inevitabilmente “gettato nel cestino”, dove il “cestino” è purtroppo l’ambiente.
Non è difficile vedere che le due formulazioni sono equivalenti:
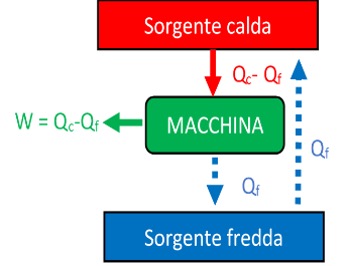
Supponiamo ad esempio di poter violare l’affermazione di Clausius. Allora (vedi figura), potremmo riportare il calore \( Q_f \) ceduto dalla macchina termica dalla sorgente più fredda a quella più calda, con il risultato netto di trasformare interamente il calore \( Q_c-Q_f \) nel lavoro \( W \).
Se invece potessimo prendere del calore dalla sorgente fredda e trasformarlo tutto in lavoro \( W \) (per esempio alzando un peso) senza cederne ad una sorgente ancora più fredda e violando quindi l’affermazione di Kelvin, potremmo usare \( W \) per scaldare la sorgente calda sfruttando ad esempio il peso sollevato per azionare un mulinello di Joule.
8. L’entropia e la freccia del tempo
Il Secondo Principio sembra quasi un’ovvietà, ma non lo è per niente. La meccanica prevede infatti che, se qualcosa avviene in una direzione, possa avvenire anche in quella opposta. Infatti, per ottenere l’accelerazione \( a \) di un corpo dividiamo un piccolo spostamento \( \Delta x=x_2-x_1 \) per \( \Delta t=t_2-t_1 \), ottenendo la velocità, e poi dividiamo ancora per \( \Delta t \) per ottenere \( a \): perciò dividiamo per \( \Delta t \) al quadrato, che è sempre positivo sia che \( t_1 \) preceda \( t_2 \), sia che lo segua. Quindi l’equazione di Newton \( F=ma \) non distingue tra passato e futuro. Ma il Secondo Principio afferma che molti fenomeni avvengono solo in una direzione: il calore passa solo dai corpi caldi ai corpi freddi e l’energia meccanica viene progressivamente dispersa in calore. In definitiva il Secondo Principio, giustificando l’esistenza di fenomeni che avvengono preferibilmente in un solo senso, che possiamo chiamare processi irreversibili, introduce una direzione del tempo dal passato al futuro.
L’esistenza di questa “freccia del tempo” è uno dei grandi misteri della fisica, solo in parte chiarito. Per capirne qualcosa, è opportuno introdurre un nuovo concetto fisico, quello di entropia, che in realtà è altrettanto importante di quello di energia. Consideriamo che cosa succede immediatamente dopo che una palla calda a temperatura \( T_c \) e una fredda a temperatura \( T_f<T_c \) vengono messe a contatto. Una piccola quantità di energia \( \Delta Q \) viene trasferita dalla palla calda a quella fredda sotto forma di calore, ma l’energia interna totale delle due palle nel complesso non cambia. Supponiamo però di rapportare il calore alla temperatura a cui viene ceduto o assorbito, ossia consideriamo la quantità \( S=Q/T \), dove \( T \) è la temperatura assoluta, che diremo proprio entropia. La palla calda perde una quantità di entropia \( \Delta S_c=-\Delta Q/T_c \) (perché il calore esce) mentre quella fredda aumenta la sua entropia di \( \Delta S_f=+\Delta Q/T_f \). Ma se ora facciamo il bilancio totale della variazione di entropia abbiamo
\( \Delta S_c+ \Delta S_f=(\frac{1}{T_f}-\frac{1}{T_f})\Delta Q>0 \)
A differenza dell’energia, l’entropia del sistema totale è aumentata! La “freccia del tempo” è proprio data dalla direzione in cui aumenta l’entropia. Risolvere l’apparente contraddizione tra meccanica e termodinamica vuol dire capire bene che cosa sia questa misteriosa entropia e perché cresca nel tempo.
9. Perché la termodinamica funziona: l’approccio statistico
Come mai la termodinamica dà ragione del comportamento dei corpi macroscopici sulla base di così pochi principi generali? Soprattutto, perché la termodinamica è in grado di descrivere i processi irreversibili, giustificando in tal modo l’esistenza di una “freccia del tempo” che le leggi della meccanica non prevede in alcun modo?
Il segreto sta proprio nel fatto che la termodinamica si occupa di sistemi costituiti da un numero enorme di atomi o molecole: ricordiamo infatti che una mole di ogni sostanza, ossia un numero di grammi pari alla sua massa molecolare, contiene infatti \( 6,22 × 10^{23} \)molecole, un numero stratosferico che è detto numero di Avogadro.
Cercare di descrivere il moto di ciascuna di queste molecole con le leggi della meccanica è ovviamente un’impresa impossibile, ma per di più non ci direbbe nulla su quelle grandezze “collettive” come la temperatura (e anche l’entropia) che abbiamo incontrato nello studio della termodinamica. L’unica alternativa è ricorrere ad un approccio statistico, cercando di ottenere almeno i valori medi, o al più la distribuzione statistica dei valori di grandezze meccaniche quali, ad esempio per un gas, l’energia cinetica delle molecole o la forza media che esercitano sulle pareti del contenitore.
10. Gas ideali e temperatura assoluta
Per sviluppare una descrizione statistica microscopica è opportuno partire da un sistema particolarmente semplice, il gas ideale (o “perfetto”), intendendo con ciò un fluido così “rarefatto” che le sue proprietà termodinamiche non dipendono più da quali atomi o molecole è composto, ma solo dalla pressione, dalla temperatura e dal volume che occupa (al più anche da quanti atomi formano una molecola del gas). Come vedremo, da un punto di vista microscopico ciò avviene quando la separazione tra due molecole del gas è in media molto grande rispetto alla distanza, o meglio al “campo d’azione”, delle forze che agiscono tra di esse. In pratica, ciò è in buona approssimazione vero anche per l’atmosfera che respiriamo.
I primi studi sui gas ideali risalgono alle osservazioni fatte da Guillaume Amontons alla fine del XVII secolo, perfezionate poi da Alessandro Volta e Joseph Louis Gay-Lussac nel secolo successivo, riguardanti la dipendenza della pressione di un gas dalla temperatura mostrarono che \( P \) dipende linearmente dalla temperatura empirica espressa in celsius, ossia
\( P=C(θ+θ_0) \)
dove \( C \) è una costante che dipende dalla densità del gas e il valore “moderno” di \( θ_0 \) (che Amontons stimò in circa 240°C) risulta proprio pari a 273.15°C. Se allora definiamo la temperatura assoluta come \( T=θ+θ_0 \), la pressione diviene semplicemente proporzionale a \( T \) e inoltre, perché si abbia \( P>0, T \) deve essere necessariamente positiva, pertanto possiamo dire che lo “zero assoluto” di temperatura è pari a -273.15°C.11. L’equazione di stato dei gas ideali
Ancor prima che Amontons enunciasse la sua legge, Robert Boyle e, indipendentemente, Edme Mariotte mostrarono che, a temperatura fissata, la pressione è inversamente proporzionale al volume del gas, ossia \( P\propto V^{-1} \). Possiamo poi aspettarci che la pressione sia ovviamente proporzionale al numero \( N \) di atomi o molecole contenute nel gas, ossia \( P \propto N \). Mettendo insieme queste osservazioni con quelle precedenti, possiamo dunque concludere che
\( P=\frac{k_BNT}{V}=ρk_BT \)
dove \( k_B \) è una costante universale detta costante di Boltzmann, data da \( k_B=1,38 \times 10^{-23}\,J/K \), e \( ρ \) è il numero di molecole per unità di volume del gas. Ricordando che \( N=nN_A \), dove \( n \) è il numero di moli e \( N_A \) il numero di Avogadro, possiamo allora scrivere anche
\( PV=nRT \)
dove \( R≃8,31 J/mol⋅K \) è detta costante dei gas. La relazione che abbiamo ottenuto è comunemente nota in entrambe le forme come “legge dei gas”, ma è più correttamente detta equazione di stato dei gas ideali.
12. Trasformazioni termodinamiche nei gas ideali
L’equazione di stato è una relazione termodinamica tra le tre variabili \( P,V,T \) (oppure \( P,ρ,T \)). Se ne fissiamo una, possiamo quindi determinare come variano le altre due l’una in funzione dell’altra. Così un gas potrà ad esempio subire una:
- trasformazione isoterma (a temperatura costante)
- trasformazione isobara (a pressione costante)
- trasformazione isocora (a volume costante)
Si possono poi rappresentare queste trasformazioni su un piano cartesiano scegliendo due delle tre variabili come assi. È spesso utile scegliere \( V \) (come ascissa ) e \( P \) (come ordinata) perché il loro prodotto è dimensionalmente un lavoro. Su un diagramma \( P,V \) una trasformazione isobara ed una isocora sono quindi semplicemente due rette parallele rispettivamente all’asse delle ascisse e a quello delle ordinate, mentre le trasformazioni isoterme sono iperbole equilatere come quelle mostrate nel disegno. Ogni punto del piano corrisponde a uno stato del gas definito dai valori di \( P,V \) e dalla temperatura corrispondente all’isoterma (unica!) che passa per quel punto.
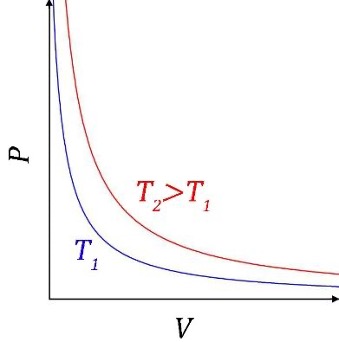
Possiamo però pensare anche a dei cambiamenti di stato in cui nessuna delle tre variabili è costante, ma \( P, V, \) e \( T \) sono comunque legate da una precisa relazione. Ad esempio, possiamo pensare ad una trasformazione in cui il gas non riceve né cede calore, che si dice adiabatica. Sul diagramma \( P,V \) l’equazione di un’adiabatica è
\( PV^ \gamma =costante \)
dove \( \gamma \) è un esponente che dipende dal tipo di gas, ed in particolare da quanti atomi formano una molecola, ma che è in ogni caso maggiore di uno (per gas monoatomici \( \gamma \)=5/3). Il pannello A nella figura a fianco mostra il confronto con un’isoterma.
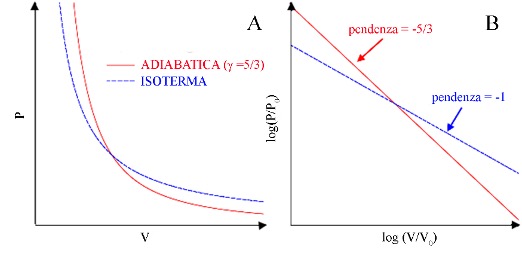
Notiamo che sia l’isoterma che l’adiabatica sono delle leggi di potenza, quindi, come mostrato nel pannello B, sono delle rette su un grafico bilogaritmico (\( V_0 \) e \( P_0 \) sono due costanti con le dimensioni di un volume e di una pressione introdotte per rendere adimensionali i logaritmi).
Dato che in una trasformazione adiabatica non si scambia calore, se questa viene compiuta molto lentamente, in modo da essere reversibile, non varia neppure l’entropia. Quindi un’adiabatica reversibile è anche una trasformazione isoentropica.
13. Cicli termodinamici, macchine termiche e frigoriferi
Vogliamo usare le trasformazioni che abbiamo introdotto per realizzare una macchina termica. Ogni macchina, dopo aver compiuto una serie di trasformazioni, deve ovviamente ritornare alle condizioni di partenza per poterle ripetere, e deve quindi operare lungo un ciclo termodinamico.
Se rappresentiamo un ciclo su di un diagramma \( pV \), l’area che esso racchiude rappresenta il lavoro netto fatto (se percorso in senso orario) o ricevuto (se percorso in senso antiorario, che è ad esempio il modo in cui funziona un frigorifero) dal sistema. Poiché alla fine il sistema torna allo stato di partenza, la variazione complessiva di energia interna lungo un ciclo è nulla. Quindi, dal Primo principio, \( Q=-W \), ossia in una macchina termica il lavoro fatto dal sistema è uguale al calore netto trasferito al sistema (mentre, per un ciclo frigorifero, facendo lavoro sul sistema, si estrae calore dal sistema).
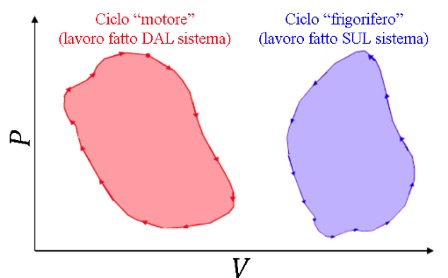
Abbiamo specificato calore “netto” perché per il Secondo Principio una parte del calore assorbito dalla macchina deve essere necessariamente trasferito ad una sorgente più fredda. Se abbiamo quindi solo due sorgenti, una calda da cui la macchina estrae una quantità di energia \( Q_c \) ed una fredda cui la macchina cede \( Q_f \) possiamo scrivere, indicando i valori assoluti del lavoro e del calore scambiati:
\( |W| = |Q_c |- |Q_f | \)
14. La “macchina ideale”: il ciclo di Carnot
Il parametro che quantifica l’efficienza di una macchina termica è il rendimento , definito come il rapporto tra il lavoro compiuto in un ciclo dalla macchina ed il calore da essa assorbito:
\( η=\frac{|W|}{|Q_c|}=1-\frac{|Q_f|}{|Q_c|} \)
Come conseguenza del Secondo Principio, \( η<1 \), ma il rendimento di una macchina termica ha in realtà un limite superiore che fu stabilito da Sadi Carnot, un ingegnere francese, fin dal 1824. Carnot stabilì che per ottenere il massimo rendimento, una macchina deve utilizzare il minimo numero possibile di sorgenti termiche, cioè due (una calda ed una fredda) e compiere un ciclo formato da quattro trasformazioni, due isoterme e due adiabatiche. Nella prima isoterma il gas viene fatto espandere a contatto con la sorgente calda, poi viene ulteriormente espanso, ma adiabaticamente, fino alla temperatura della sorgente fredda, quindi viene compresso a contatto con la sorgente fredda, ed infine viene ulteriormente compresso adiabaticamente fino a ritornare alla stato di partenza (si veda la figura qui sotto, dove il ciclo di Carnot è rappresentato in un diagramma log-log).
Il rendimento è massimo solo se ognuna delle trasformazione è “quasi” reversibile, ossia se la temperatura della macchina differisce di pochissimo da quella delle sorgenti con cui viene messa a contatto, e se le trasformazioni adiabatiche avvengono molto lentamente. In questo caso \( η \) dipende solo dal rapporto \( \dfrac{|Q_f |}{|Q_c |} \).
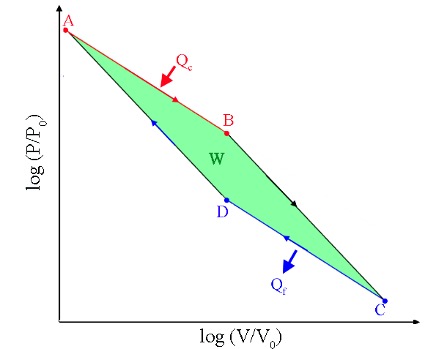
Successivamente Kelvin e Joule mostrarono che nel ciclo di Carnot ideale il rapporto tra i calori scambiati con le due sorgenti può essere scritto semplicemente come rapporto delle temperature delle due sorgenti, purché queste vengano misurate proprio su quella scala “assoluta” che aveva avuto origine dallo studio delle leggi dei gas. Ovverosia, misurando le temperature in kelvin, si ha:
\( η=1-\dfrac {T_f}{T_c} \)
15. Un tuffo nel mondo microscopico: la teoria cinetica dei gas
Cerchiamo di comprendere come il comportamento macroscopico del gas possa essere spiegato da un modello microscopico con una breve introduzione a quella che si chiama “teoria cinetica” dei gas, originariamente sviluppata da James Clark Maxwell.
Descriveremo un gas ideale come un sistema di palline che interagiscono solo con urti elastici e che hanno una dimensione molto minore della distanza media tra di esse. Di conseguenza, gli urti avvengono solo occasionalmente, mentre per la maggior parte del tempo le palline si muovono di moto uniforme in tutte le direzioni, naturalmente non tutte allo stesso modo ma con una certa distribuzione delle velocità.
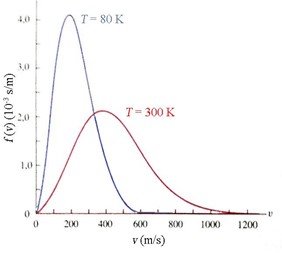
Maxwell, facendo pochissime assunzioni sulle proprietà che deve avere la distribuzione delle velocità all’equilibrio (ad esempio che non deve dipendere dalla direzione o dal verso della velocità stessa) riuscì a ottenerne l’andamento mostrato in figura, giustamente detto distribuzione maxwelliana. Al crescere della temperatura il picco si sposta verso valori più alti e si allarga. Quindi anche il valor medio di \( v \) (e pertanto l’energia cinetica media del gas) cresce con la temperatura. Per l’esattezza, Maxwell trovò che il valore medio dell’energia cinetica di un gas monoatomico costituito da \( N \) atomi gas vale:
\( \overline E_c=\frac32Nk_B T \)
Se interpretiamo questa energia cinetica come energia interna \( U \) del gas, ne segue che la capacità termica di un gas monoatomico è pari a \( \frac 32Nk_B \), valore in ottimo accordo con i dati sperimentali. Tenendo conto dell’equazione di stato per i gas ideali (che viene pienamente giustificata dal modello di Maxwell), si ottiene infine
\( PV=\frac 23 U \)
Successivamente Ludwig Boltzmann mostrò come un gas che parta da una condizione qualunque, anche molto lontana dall’equilibrio, raggiunge col tempo la distribuzione delle velocità trovata da Maxwell. Ciò avviene quando una certa grandezza, che dipende dalla funzione di distribuzione delle velocità, raggiunge il suo massimo valore. Questa grandezza è l’equivalente microscopico dell’entropia termodinamica ed il suo andamento giustifica, almeno in senso statistico, l’esistenza di una direzione del tempo.