Il fissaidee
| Site: | Federica Web Learning - LMS |
| Course: | Scienze fisiche di base |
| Unit: | Il fissaidee |
| Printed by: | Guest user |
| Date: | Tuesday, 26 August 2025, 8:24 PM |
Table of contents
- 1. Elettricità e magnetismo
- 2. Campo elettrico e legge di Gauss
- 3. Lavoro. energia potenziale e potenziale elettrico
- 4. Condensatori e capacità
- 5. Corrente elettrica, resistenza e effetto Joule
- 6. Resistenza equivalente, circuiti e forza elettromotrice
- 7. I magneti permanenti e il campo magnetico
- 8. Effetti magnetici delle e sulle correnti elettriche
- 9. Induzione elettromagnetica e campo elettromagnetico
1. Elettricità e magnetismo

Settima tappa
Carica elettrica, conduttori e isolanti
Introduciamo ora dei nuovi fenomeni e delle nuove quantità fisiche, iniziando con la carica elettrica. Sperimentalmente si osserva che alcuni materiali (detti isolanti) possono essere “caricati”, ad esempio strofinandoli con un panno asciutto, in modo tale che respingono materiali dello stesso tipo, a loro volta “caricati”, e ne attraggono invece di tipo diverso, “caricati” anch’essi. Da questa ed altre evidenze si è stabilita l’esistenza di due tipi diversi di cariche elettriche, cariche positive e cariche negative, con cariche dello stesso segno che si respingono e cariche di segno opposto che si attraggono.
Si nota anche che non tutti i materiali possono essere caricati nello stesso modo: il caricamento che abbiamo descritto funziona per vetro, gomma, resine varie, bachelite etc., ma non funziona per i materiali di tipo metallico. La ragione è che esistono materiali in cui le cariche sono pochissimo mobili e restano quindi nella posizione dove sono state depositate, detti isolanti, e materiali dove le cariche si muovono liberamente, i conduttori, alla cui classe appartengono i metalli.
Se si deposita della carica su di un conduttore questa si muoverà fino a disporsi esclusivamente sulla superficie del conduttore; questo comportamento risulta abbastanza intuitivo se si pensa che le cariche dello stesso segno si respingono e quindi per allontanarsi il più possibile le une dalle altre raggiungeranno la superficie del conduttore, non potendo diffondersi nell’aria circostante, che è un isolante.
Date due cariche \( q_1 \) e \( q_2 \), l’intensità della forza che si esercita fra di esse è data dalla legge di Coulomb:
\( F=\dfrac{1}{4 \pi \epsilon _0}\dfrac{q_1q_2}{r^2} \)
Dove \( r \) è la distanza fra le cariche, \( \epsilon_0 \) è detta costante dielettrica (o “permittività elettrica”) del vuoto, e le cariche sono misurate in coulomb (C), una nuova unità di misura del Sistema Internazionale oggi definita in termini della carica più piccola presente in natura, quella di un elettrone: indicando il valore assoluto di quest’ultima con \( e \), si ha \( 1C \simeq 6,2410^{18}e \). In queste unità, Il valore della costante dielettrica del vuoto è
\( \epsilon _0 \simeq 8,8510^{-12}C^{2}N^{-1}m^{-2} \)
Per spostarti tra le pagine del fissaidee utilizza le frecce azzurre.
2. Campo elettrico e legge di Gauss
Introduciamo ora un concetto molto utile, quello di campo elettrico. Supponiamo di essere in presenza di diverse cariche che interagiscono fra di loro tramite le forze di Coulomb: in ogni punto \( r \) dello spazio potremo esplorare l’effetto dell’intera distribuzione di cariche collocando in quel punto una carica \( q \) abbastanza piccola da non modificare la distribuzione spaziale delle cariche stesse. Detta \( \textbf{F}(r) \) la forza di Coulomb agente su questa “carica di prova” chiameremo campo elettrico nel punto \( r \) il vettore
\( E(r)=\dfrac{F(r)}{q} \)
che ci permette di valutare la forza che agisce su una qualsiasi carica elettrica collocata nello spazio. Si può rendere visivamente l’andamento del campo in ogni punto, tracciando le linee di campo la cui direzione e verso corrispondono a quella della forza agente su di una carica positiva posta nel punto considerato.
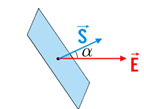
Possiamo quantificare quanto si “addensino” nello spazio le linee di campo per mezzo del concetto di flusso del campo elettrico attraverso una superficie. Consideriamo un campo \( E \) costante e una superficie piana che rappresenteremo come un vettore \( S= Sn \) orientato secondo la normale \( n \) alla superficie, e definiamo il flusso \( \Phi_S ( E ) \) del campo \( E \) attraverso \( S \) come il prodotto scalare di \( E \) con \( S \):
\( \Phi _S(E)=E⋅S=ES\,cos\,\, \alpha \)
Il concetto di flusso può essere applicato a qualsiasi vettore, non solo al campo elettrico. Per il campo elettrico, che è proporzionale a \( \dfrac1{r^2} \), si può però dimostrare (teorema di Gauss) che il flusso attraverso una qualsiasi superficie chiusa è dato semplicemente dalla somma algebrica delle cariche che si trovano all’interno della superficie, divisa per la costante dielettrica:
\( \Phi _S(E)= \dfrac{ \sum{q_i} }{ \epsilon_0 } \)
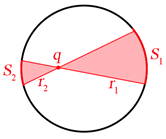
La ragione di fondo per cui il flusso dipende solo dalla carica totale e non da dove si trovano le singole cariche è che il campo elettrico decresce con il quadrato della distanza dalle cariche che lo generano. È facile intuirlo se consideriamo una singola carica all’interno di una sfera come nella figura a fianco: il campo su \(S_1 \)è infatti ridotto rispetto a quello su \( S_2 \) di un fattore \( (\dfrac{r_2}{r_1} )^2 \), ma d’altronde l’area di \( S_1 \) è a sua volta più grande di quella di \( S_2 \) di un fattore \( (\dfrac{r_1}{r_2} )^2 \), per cui il flusso attraverso le due superfici è lo stesso dovunque si trovi \( q \).
Utilizzando il teorema di Gauss si può facilmente calcolare il campo elettrico per distribuzioni di carica che presentino simmetrie. Ad esempio, a distanza r da un filo infinitamente lungo con densità di carica per unità di lunghezza si trova che l’intensità del campo elettrico vale \( E= \dfrac{\lambda }{2 \pi \epsilon_0r } \), mentre nelle vicinanze di una superficie piana con densità di carica \( \lambda \) per unità di superficie l’intensità del campo elettrico vale \( E= \dfrac{ \sigma }{2 \pi \epsilon_0 } \).
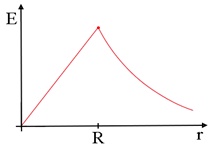
Una distribuzione sferica di carica di raggio \( R \) genera al suo esterno un campo elettrico identico a quello che sarebbe generato se tutta la carica fosse concentrata al centro della sfera, mentre all’interno il campo cresce linearmente con la distanza r dal centro, come in figura.
3. Lavoro. energia potenziale e potenziale elettrico
La forza di Coulomb dipende dall’inverso del quadrato della distanza, esattamente come la forza di gravità, che è una forza conservativa. Quindi anche il lavoro \( L \) compiuto dalla forza di Coulomb non dipenderà dal percorso, ma solo dai punti iniziale e finale \( r_1 \) ed \( r_2 \), e potrà essere espresso come la differenza dei valori in \( r_1 \) ed \( r_2 \) di una funzione \( U_r \) che diremo energia potenziale elettrostatica:
\( L= \Delta U(r)=U(r_2)-U(r_1). \)
Così come abbiamo definito il campo elettrico a partire dalla forza di Coulomb dividendola per (“normalizzandola” alla) carica che la produce, possiamo introdurre il potenziale elettrostatico
\( V(r)= \frac{U (r)}{q} \)
per cui il lavoro compiuto dal campo generato da \( q \) su una carica \( q’ \) si scrive anche \( L=q' \Delta V \). Nel Sistema Internazionale l’unità di misura del potenziale è il volt, dato dal rapporto joule su coulomb, \( 1\textbf{V}=1(\textbf{J/C)} \).
4. Condensatori e capacità
Il condensatore è un componente elettrico che permette di accumulare cariche elettriche, e pertanto energia elettrostatica, su delle superfici metalliche dette armature. Ad esempio possiamo considerare come armature due lastre metalliche piane disposte parallelamente con l’intercapedine fra le lastre vuota o, più comunemente, riempita di un materiale isolante (“dielettrico”): se carichiamo una delle due piastre con una carica positiva o negativa, per un fenomeno detto induzione l’altra si carica a sua volta con una quantità di carica uguale ma opposta in segno. La carica \( Q \) accumulata dà origine ad una differenza di potenziale
\( \Delta V=\frac QC \)
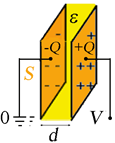
Dove la quantità \( C \), detta capacità, dipende dalla geometria del condensatore e dalla costante dielettrica \( ε \) del mezzo interposto fra le armature. La capacità di un condensatore piano a facce parallele come quello in figura è ad esempio data da \( C=\dfrac{εS}d \). L’unità di misura della capacità è il farad, pari a coulomb su volt, \( 1\textbf{F} =1(\textbf{C/V}) \). Notate che l’inserimento del dielettrico aumenta la capacità del condensatore rispetto a quella che avrebbe se vi fosse il vuoto, perché per tutti i materiali \( ε>ε_0 \).
5. Corrente elettrica, resistenza e effetto Joule
Come abbiamo anticipato, in un conduttore come un metallo la carica può muoversi liberamente. Se agli estremi di un filo metallico viene applicata una differenza di potenziale, questa genererà una corrente \( I \), definita come il rapporto fra la quantità di carica \( \Delta Q \) che attraversa la sezione del filo in un intervallo di tempo \( \Delta T \) e \( \Delta T \) stesso:
\( I=\frac{ \Delta Q} { \Delta T} \)
Nel Sistema Internazionale la corrente si misura in coulomb al secondo, unità detta ampere (A). Il verso della corrente è convenzionalmente definito come quello in cui si muovono le cariche positive, anche se in realtà nei conduttori le cariche libere di muoversi sono gli elettroni, che hanno carica negativa.
Nei metalli (ma non in altri mezzi come ad esempio i semiconduttori) la relazione fondamentale che lega la corrente \( I \) alla differenza di potenziale \( V \) applicata è la legge di Ohm, la quale stabilisce semplicemente che queste due quantità sono proporzionali attraverso quella che viene detta resistenza \( R \) del conduttore:
\( V=RI \)
quantità che si misura in volt/ampere, unità detta ohm ed indicata con \( \Omega \) (Omega) che dipende dalla geometria del conduttore e da un parametro specifico \( \sigma \) del materiale di cui è costituito detto conducibilità. Nel caso di un filo metallico di lunghezza \( l \) e sezione \( A \) si ha ad esempio \( R=l/σA \). Dato che l’intensità \( E \) del campo elettrico nel filo è data dal rapporto \( V/l \), la legge di Ohm ci dice che il flusso \( J \) di corrente nel conduttore (ossia la corrente attraverso una sezione unitaria) è proporzionale al campo elettrico: \( J=σE \).
La presenza di una resistenza al passaggio di corrente implica che l’energia fornita alle cariche dalla differenza di potenziale viene dissipata. Per un conduttore che soddisfi la legge di Ohm la potenza dissipata è data dalla legge di Joule:
\( P=VI=\frac {V^2}{R}=RI^2 \)
l’energia dissipata riscalda il conduttore per quello che viene detto effetto Joule. Notiamo che, per una fissata differenza di potenziale applicata, la potenza dissipata è tanto maggiore quanto minore è la resistenza del conduttore.
6. Resistenza equivalente, circuiti e forza elettromotrice
Un componente che viene utilizzato come elemento resistivo in un circuito elettrico viene detto resistore, e più resistori possono essere combinati fra loro in modo da ottenere una resistenza equivalente complessiva del circuito. Se consideriamo due soli resistori, questi possono essere collegati:
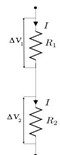
- in serie, quando i resistori sono posti l’uno dopo l’altro sullo stesso percorso e sono quindi attraversati dalla stessa corrente I, mentre ai loro capi si hanno cadute di potenziale diverse \( \Delta V_1=R_1I, \Delta V_2=R_2I. \) In questo caso la resistenza equivalente \( R \) è data dalla somma delle due resistenze:
\( R=R_1+R_2 \)
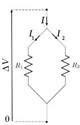
- In parallelo, quando ai capi dei resistori viene applicata la stessa differenza di potenziale V e la corrente I si dirama in percorsi diversi che attraversano le due resistenze. In questo caso l’inverso della resistenza equivalente è dato dalla somma degli inversi delle due resistenze:
\( \frac1R=\frac 1{R_1}+\frac 1{R_2} \)
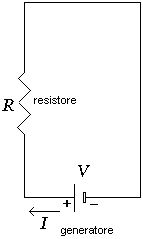
Per far circolare corrente in un circuito che dissipa potenza per effetto Joule in uno o più resistori è ovviamente necessario fornire energia attraverso una sorgente detta generatore di forza elettromotrice (ad esempio una semplice pila zinco/carbone, o una batteria al litio) che genera ai suoi capi la differenza di potenziale che fa fluire la corrente nel circuito. L’unità di misura della forza elettromotrice (f.e.m.) di un generatore è quindi la stessa del potenziale elettrico, ossia il volt. Il più semplice circuito elettrico è quindi costituito da un generatore di f.e.m. e da un resistore, come nella figura qui sotto.
Ovviamente i circuiti possono essere molto più complessi di quello semplicissimo visto sopra.
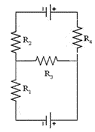
Ad esempio, potremmo considerare un circuito con due “maglie” come quello qui sotto, nel quale vediamo dei nodi, cioè dei punti in cui ci sono più correnti in ingresso e/o uscita. Per questi punti vale una semplice legge dei nodi: l’intensità di corrente entrante in un nodo sarà uguale alla somma delle intensità di corrente uscenti, regola che deriva immediatamente dalla conservazione della quantità di carica che attraversa il conduttore in quel punto. Per determinare la corrente che circola in ogni tratto dovremo usare anche la legge delle maglie che stabilisce che la somma algebrica di tutte le differenze di potenziale in una maglia è zero, che corrisponde principio di conservazione dell’energia.
7. I magneti permanenti e il campo magnetico
In natura esistono materiali, come ad esempio la magnetite (una roccia vulcanica), che “attirano” alcuni metalli come il ferro, il nickel e pochi altri: è con questi materiali che furono realizzate le prime “calamite” o “magneti” e gli aghetti utilizzati nelle prime bussole, note già ai navigatori cinesi ben prima del medioevo, capaci di individuare il punto cardinale Nord (ma solo approssimativamente, perché il Polo Nord “magnetico” non coincide con quello geografico).
I materiali come il ferro o il nickel che vengono attirati da una calamita si magnetizzano a loro volta e rimangono magnetizzati anche dopo che il magnete viene allontanato: questi materiali sono detti ferromagneti. Materiali come l’alluminio nei quali l’effetto di magnetizzazione è molto più debole e scompare quando la calamita viene allontanata vengono detti paramagneti. Esistono anche materiali come la grafite, detti diamagneti, che vengono debolmente respinti da una calamita (le proprietà magnetiche della materia hanno origine da complicati fenomeni legati alla natura delle particelle che costituiscono gli atomi, e in particolare da una proprietà detta “spin”, su cui per il momento non possiamo dire molto).
Abbiamo visto che la carica elettrica può essere positiva o negativa. Anche per un magnete si possono fenomenologicamente definire due diversi “poli”, nord (N) e sud (S): se si avvicinano due magneti, i poli dello stesso tipo si respingono, mentre quelli di tipo opposto si attraggono. C’è però una differenza fondamentale tra poli magnetici e cariche elettriche: se si spezza un magnete, ciascuno dei due magneti che si ottengono presenta ancora sia il polo N che dal polo S: in altre parole, non c’è nessun modo di ottenere un “monopolo” magnetico, cioè una sorgente del campo magnetico di un solo tipo.
Anche per i magneti possiamo introdurre un concetto di campo magnetico come un vettore la cui direzione in ogni punto è quella lungo cui si orienta l’ago di una bussola e la cui intensità è proporzionale alla densità delle sue linee di forza, che possono ad esempio essere visualizzate cospargendo una superficie su cui il magnete è appoggiato con della limatura di ferro. Il fatto che sia impossibile separare il polo nord dal polo sud fa sì che le linee di campo magnetico siano linee chiuse: ciò implica che il flusso di campo magnetico attraverso qualsiasi superficie chiusa è sempre nullo.

8. Effetti magnetici delle e sulle correnti elettriche
Per quanto noti fin dall’antichità, i fenomeni magnetici furono avvolti per lungo tempo da un’aura di mistero, perché non sembravano connessi a nessun altro fenomeno fisico. D’altronde, espressioni come “sguardo magnetico” o “magnetismo animale” (detto anche “mesmerismo”, per via delle pseudo-terapie basate sull’azione di magneti utilizzate da Franz Anton Mesmer, medico tedesco del ‘700) sopravvivono ancora nella nostra lingua.
A partire dai primi anni del XIX secolo tuttavia, cominciarono ad accumularsi evidenze che mettevano in relazione i campi magnetici con le correnti elettriche, cioè con la presenza di cariche in moto. Così si osservò che:
- Un filo percorso da corrente elettrica genera un campo magnetico (1820, Hans Christian Ørsted);
- Tra due fili percorsi da corrente si esercita una forza, attrattiva se le correnti sono equiverse e repulsiva se le correnti scorrono con versi opposti (1826, André-Marie Ampère);
- Un campo magnetico genera una forza su di un filo percorso da corrente (1831, Michael Faraday).
Più quantitativamente, la legge di Ampère afferma che la forza tra due fili di lunghezza \( L \) in cui scorrono correnti di intensità \( i_1 \) e \( i_2 \) è data da
\( F=\dfrac {\mu _{0}}{2π}\dfrac{i_1i_2}dL \)
dove μ0 è una costante detta permeabilità magnetica del vuoto (l’analogo di \( \epsilon_0 \) nella legge di Coulomb).
La legge di Ampère ci fa intuire che una corrente generi di fatto un campo magnetico. Questo effetto può essere amplificato avvolgendo un filo in una bobina con tante spire e costruendo in tal modo un solenoide, che quando percorso da corrente produce un campo magnetico, esattamente come farebbe un magnete. Questo campo può essere reso ancora più intenso ponendo all’interno del solenoide un materiale magnetizzabile (un “traferro”).
Dato che in fin dei conti una corrente elettrica non è altro che cariche in movimento, il fatto che un filo percorso da corrente sia soggetto agli effetti di un campo magnetico (legge di Faraday) suggerisce che una carica \( q \) che si muove in un campo magnetico \( B \) con una certa velocità \( v \) subisca una forza: questa forza esiste ed è data da
\( F_m=q v\times B \)
Notate che è una forza molto particolare perché, oltre che alla direzione del campo magnetico, è sempre perpendicolare alla velocità, e quindi allo spostamento della carica: ciò però significa che le forze dovute ai campi magnetici non fanno mai lavoro (che è il prodotto scalare di forza e spostamento) sulle cariche, ossia non cambiano la loro energia cinetica (ossia solo la direzione, ma non il modulo della velocità)!
Nel caso in cui oltre al campo magnetico sia presente anche un campo elettrico, la forza totale agente su una carica, detta forza di Lorentz, è quindi data nel Sistema Internazionale da:
\( F=q(E+v\times B ) \)
C’è però un aspetto davvero “inquietante” nel termine della forza di Lorentz dovuto al campo magnetico: mentre esiste per un osservatore 1 che vede la carica muoversi con velocità \( v \), per un osservatore 2 che si muove con la stessa velocità di \( q \), \( F_m \) è nulla. Ma se \( v \) è costante gli osservatori 1 e 2 sono in moto rettilineo uniforme l’uno rispetto all’altro e quindi, per il principio d’inerzia, dovrebbero vedere le stesse forze! Le forze magnetiche sembrano quindi violare il principio fondamentale su cui abbiamo costruito tutta la fisica…che succede?
Avremmo potuto intuire qualcosa se, invece del Sistema Internazionale, tanto amato dagli sperimentali, avessimo usato il vecchio sistema c.g.s. di Gauss, che continua ad essere il favorito da parte di molti fisici teorici. Nel caso dell’elettricità e del magnetismo infatti i due sistemi non differiscono solo per le unità di misura, ma per la stessa espressione delle leggi fondamentali. Ad esempio, nel sistema di Gauss la legge di Coulomb si scrive semplicemente \( F=q_1q_2/r^2 \), senza nuove costanti (dimensionali) come \( \epsilon_0 \) , per cui non c’è bisogno di introdurre nuove unità fondamentali come il coulomb: le dimensioni di q sono proprio fissate dalla legge di Coulomb in una lunghezza per la radice di una forza. Nel sistema di Gauss la forza di Lorentz si scrive:
\( F=q(E+\dfrac vc \times B) \)
dove \( c \) è la velocità con cui si muove la luce nel vuoto, che nella lezione 8 vedremo essere gigantesca: 3× 108 m/s. Da ciò vediamo che gli effetti dovuti al campo magnetico diventano apprezzabili rispetto a quelli dovuti al campo elettrico solo quando la carica si muove ad una velocità confrontabile con quela della luce. Questo è il dominio di una nuova teoria che ha rivoluzionato la fisica, la teoria della relatività ristretta di Albert Einstein, che corregge opportunamente il principio di inerzia di Galileo, ma che purtroppo in questo corso introduttivo non abbiamo il tempo ed il modo di raccontarvi…
9. Induzione elettromagnetica e campo elettromagnetico
Faraday scoprì molto di più della semplice legge esposta nella slide precedente, osservando che se si fa variare nel tempo un campo magnetico, per esempio allontanando ed avvicinando periodicamente un magnete ad una filo metallico che si richiude su se stesso formando un circuito chiuso, si induce nel filo una corrente anche se nel circuito non vi è alcun generatore di forza elettromotrice. Il verso della corrente che si genera è tale da “opporsi” alla variazione del campo magnetico, nel senso che tale corrente genera a sua volta un campo magnetico diretto in senso opposto a quello che la eccita. In termini quantitativi, è come se nel circuito fosse presente una forza elettromotrice “indotta” data da
\( (f.e.m.)_{ind}=-\dfrac { \Delta \Phi_ B}{ \Delta t} \)
Dove \( \Phi_ B=B\cdot S \) è il flusso di \( B \) attraverso la superficie racchiusa dal circuito.
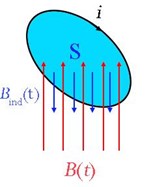
Sugli effetti di induzione magnetica scoperti da Faraday si basano molti dispositivi di uso comune come le dinamo e gli alternatori; di fatto, la produzione di una frazione consistente dell’energia elettrica che utilizziamo è basata sulla rotazione di bobine poste in un campo magnetico. Ma, al di là delle sue innumerevoli applicazioni, il contenuto fisico fondamentale della legge di induzione è che un campo magnetico variabile nel tempo genera un campo elettrico (quello che muove gli elettroni nel circuito).
Fu Maxwell a cogliere in pieno questo aspetto e a dare una forma matematica precisa alle osservazioni sperimentali di Faraday. Maxwell ebbe però anche un’altra intuizione: così come la variazione nel tempo di un campo magnetico genera un campo elettrico, anche un campo elettrico variabile nel tempo deve generare un campo magnetico. L’esistenza di quest’effetto (più complesso da spiegare, ma che è sostanzialmente necessario per rendere consistente la legge di Ampère nel caso di correnti variabili) permette di immaginare che anche in assenza di cariche e correnti possa esistere un campo elettrico che, variando nel tempo, genera un campo magnetico il quale, anch’esso variabile nel tempo, generi a sua volta un campo elettrico: in altri termini, porta a concepire l’esistenza di campi elettromagnetici che si “autosostengono”, che come vedremo sono ciò che dà origine a quella che nella lezione 8 chiameremo radiazione elettromagnetica, e che è forse la conseguenza più importante della grande sintesi dei fenomeni elettrici e magnetici operata da Maxwell.