Il fissaidee
| Sito: | Federica Web Learning - LMS |
| Corso: | Scienze fisiche di base |
| Unit: | Il fissaidee |
| Stampato da: | Utente ospite |
| Data: | martedì, 26 agosto 2025, 20:24 |
Indice Unit
- 1. Propagazione della luce e indice di rifrazione
- 2. Le leggi dell’ottica geometrica: riflessione e rifrazione
- 3. Le lenti e la formazione delle immagini
- 4. Le immagini virtuali
- 5. La natura ondulatoria della luce
- 6. La diffrazione
- 7. Interferenza
- 8. Dall’esperienza di Young ai reticoli di diffrazione
- 9. Dalle dispersione allo spettro delle onde elettromagnetiche
1. Propagazione della luce e indice di rifrazione

Ottava tappa
L’ottica geometrica assume che la luce si propaghi in linea retta (il che ci permette di introdurre il concetto di raggio di luce) con una velocità che, nel vuoto, è data da \( c \simeq 3 \times 10^8\, m/s \). Di fatto, nel Sistema Internazionale c è assunta come esattamente uguale a \( 299.792.458 \, m/s \), perché è tramite di essa che si definisce il metro!
La velocità di propagazione in un mezzo materiale è pari a \( c/n \), dove n è un parametro specifico del mezzo considerato detto indice di rifrazione che, sempre in ottica geometrica, è sempre maggiore di uno, per cui la luce viaggia sempre più piano che nel vuoto. Quando discuteremo la natura ondulatoria della luce, vedremo che l’indice di rifrazione di un materiale dipende in realtà dalla lunghezza d’onda (quindi dal “colore”) della luce, fenomeno che prende il nome di dispersione. Esistono naturalmente mezzi, in particolare i metalli, in cui la luce non si può propagare: dal punto di vista dell’ottica geometrica ciò equivale a porre \( n= \infty \).
Per spostarti tra le pagine del fissaidee utilizza le frecce azzurre.2. Le leggi dell’ottica geometrica: riflessione e rifrazione
Quando un raggio di luce che si propaga in un mezzo 1 che ha indice di rifrazione \( n_1 \) raggiunge la superficie di separazione (o ”interfaccia”) con un mezzo 2 che ha indice di rifrazione \( n_2 \neq n_1 \) si suddivide, in generale, in un raggio riflesso, ossia “rispedito” nel mezzo 1, ed in uno rifratto, che si propaga nel mezzo 2 ma con una direzione differente.
Per determinare la direzione del raggio riflesso e di quello rifratto è conveniente riferirci alla perpendicolare nel punto di contatto alla superficie di separazione (che può essere anche curva). Così facendo si ha (si veda la figura):
- Riflessione: l’angolo di incidenza è uguale a quello di riflessione \( \theta_1 = \theta ' _1 \)
- Rifrazione (legge di Snell): \( n_1sen \theta _1 =n_2sen \theta _2 \)
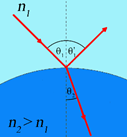
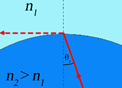
Se il raggio proviene dal mezzo con l’indice di rifrazione maggiore allora, poiché \( sen \theta_1 \leq 1 \), c’è un angolo critico di incidenza \( \theta_c \) oltre il quale il raggio incidente viene completamente riflesso. Tale condizione di riflessione interna totale sarà quindi data da \( \theta_c=n_1/n_2 \)
3. Le lenti e la formazione delle immagini
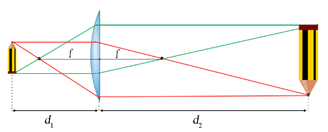
Possiamo sfruttare il fenomeno della rifrazione per “concentrare” un fascio di raggi di luce paralleli in quello che in ottica geometrica è idealmente un punto P, detto “fuoco”. Questo è ciò che fa una lente convergente, che è costituita da un dischetto di materiale trasparente limitato da due superfici, di cui almeno una convessa, con indice di rifrazione maggiore di quello del mezzo in cui viene posto (generalmente l’aria, dove \( n=1 \), ma potrebbe anche essere un liquido come l’acqua, in cui \( n≃ 4/3 \)). Ogni lente convergente è infatti caratterizzata da una lunghezza focale \( f \), che corrisponde proprio alla distanza dalla lente (supposta sottile, cioè di spessore molto minore di \( f \)) in cui un fascio di luce viene messo a fuoco.
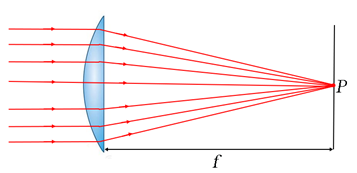
Una lente di questo tipo può essere utilizzata per formare una immagine reale di un oggetto, dove per “reale” intendiamo che si può ad esempio proiettare su uno schermo. Se infatti poniamo un oggetto ad una distanza \( d_1 \) dalla lente, dall’altra parte si forma un immagine dell’oggetto ad una distanza \( d_2 \) che è legata a \( d_1 \) e a \( f \) dalla legge della lente sottile (detta anche “equazione degli ottici”):
\( \dfrac1{d_1}+ \dfrac1{d_2}=\dfrac 1f \)
L’immagine risulta rovesciata ed ingrandita (o ridotta) del fattore \( d_2/d_1 \). Notiamo poi che un’immagine reale si può formare solo se \( d_1>f \).
4. Le immagini virtuali
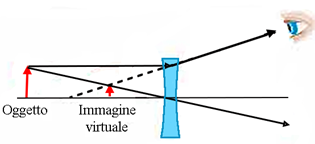
Una lente divergente come quella mostrata in figura, presenta invece un fuoco “apparente” (perché in questo caso in esso non si concentra la luce) che sta davanti alla lente, cioè dalla parte del fascio incidente. In questo caso non si possono formare immagine reali. Tuttavia il nostro occhio, prolungando i raggi che divergono dalla lente, ha l’impressione che si formi effettivamente un’immagine, ma dalla stessa parte dell’oggetto rispetto alla lente: questa è detta immagine virtuale, e naturalmente non può essere proiettata su nessun supporto, perché di fatto è solo un’illusione creata dal nostro occhio. È interessante notare che la “legge della lente” permette ancora di calcolare dove si troverà l’immagine, purché si assuma un valore negativo per \( f \). In questo caso, sarà ovviamente negativo anche \( d_2 \), che significa che anche l’immagine virtuale si trova davanti alla lente.
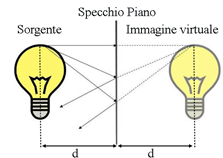
Un caso particolarmente interessante di immagine virtuale è quella prodotta da uno specchio piano, ossia da una superficie di vetro metallizzata completamente riflettente (notate che, mentre negli specchi domestici il vetro si trova davanti al metallo a scopo di protezione, negli specchi usati in uno strumento ottico come un telescopio la metallizzazione è fatta sulla faccia anteriore, mentre il vetro ha solo funzione di supporto!). In questo caso l’immagine virtuale appare dietro lo specchio e l’ingrandimento è unitario.
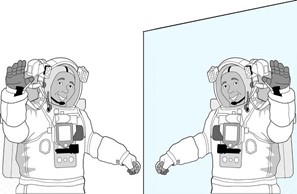
Chiudiamo questa breve carrellata sull’ottica geometrica (ci sarebbe ancora tanto da dire!) con uno spunto di riflessione, che riguarda proprio gli specchi. Siamo soliti dire che uno specchio “scambia la destra con la sinistra”…ma perché non “l’alto col basso”? In fondo ciò che distingue destra/sinistra da alto/basso è solo la direzione della forza di gravità. Ma che ne sa lo specchio della gravità? E che cosa succede quando un astronauta si specchia a bordo della Stazione Spaziale? Per capire che in realtà le due affermazioni sono equivalenti, provate a pensare bene che cosa intendete quando dite che uno specchio scambia la destra con la sinistra…
5. La natura ondulatoria della luce
La luce ha in realtà una natura ondulatoria, ossia presenta tutte le proprietà che abbiamo introdotto per le onde meccaniche, come lunghezza d’onda e frequenza. Normalmente è difficile accorgersene, tanto è vero che le semplici leggi dell’ottica geometrica sono sufficienti a spiegare molte delle osservazioni quotidiane, e questo perché la lunghezza d’onda della luce è molto piccola, dell’ordine dei decimi di micrometro. Diverse lunghezze d’onda vengono percepite dall’occhio come diversi colori. In particolare, il rosso cupo ed il blu/violetto corrispondono rispettivamente alla massima e alla minima lunghezza d’onda che l’occhio è in grado di percepire. È importante osservare che all’interno di un materiale che abbia indice di rifrazione \( n \) la lunghezza d’onda diviene \( \lambda= \lambda_0/n \), dove \( \lambda_0 \) è la lunghezza d’onda nel vuoto (mentre la frequenza \( v \) non cambia).
6. La diffrazione
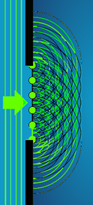
La natura ondulatoria della luce si rivela quando questa incontra aperture di dimensioni che cominciano ad essere non molto maggiori della sua lunghezza d’onda. In questo caso, la luce non si propaga più in linea retta, ma viene diffratta lungo direzioni diverse da quella originale. Ad esempio, nel passaggio attraverso di una fenditura verticale in uno schermo opaco di larghezza \( d \) come quella in figura (vista dall’alto), il fascio di luce si apre in un “ventaglio” di direzioni di propagazione diverse che è tanto più ampio quanto più grande è il rapporto \( \lambda/d \).
Per ricostruire qualitativamente l’onda trasmessa al di là della fenditura è utile far uso del principio di Huygens, secondo il quale ogni punto della fenditura può essere considerato come sorgente di un’onda sferica “secondaria” con ampiezza proporzionale a quella dell’onda incidente: il fronte d’onda che si propaga oltre la fenditura è la “somma” (ossia l’inviluppo) di tutte queste onde secondarie.

7. Interferenza
Per “sommare” i contributi delle sorgenti secondarie introdotte dal principio di Huygens in modo da ottenere correttamente l’ampiezza e l’intensità dell’onda risultante, dobbiamo tenere conto del fatto che le onde interferiscono. Come abbiamo visto nella quarta lezione, infatti, se sovrapponiamo due onde di uguale ampiezza \( A \) che oscillano sinusoidalmente alla stessa frequenza angolare \( ω=2πν=2πc/λ \) e con lo stesso vettore d’onda \( k=\frac{2π} \lambda \), ma con fasi (ossia l’argomento del seno) che differiscono di \( φ \) l’ampiezza risultante non è in generale \( 2A \), ma è determinata anche dalla loro fase relativa. Infatti, dalla formula generale \( sen(p)+sen(q)=2cos(\dfrac {p-q}2) sen(\dfrac {p+q}2) \) abbiamo:
\( y_1+y_2=Asen(kx- \omega t) +Asen(kx- \omega t+φ)=2Acos(\fracφ2)sen(kx-ωt+\fracφ2) , \)
per cui l’ampiezza risultante è pari a \( 2A \) solo se \( φ=0 \), ossia se le due onde sono “in fase”, ma può essere addirittura nulla se \( φ=π \), ossia se le due onde sono “in opposizione di fase”.
Se poi ricordiamo che l’intensità di un’onda, ossia la sua potenza per unità di superficie, è proporzionale al quadrato dell’ampiezza, vediamo che l’intensità dell’onda risultante varia tra 0 e quattro volte quella di ciascuna delle due onde.
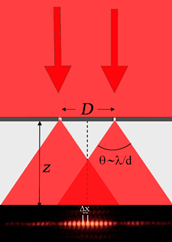
8. Dall’esperienza di Young ai reticoli di diffrazione
Un esperimento interessante in cui possiamo notare l’effetto combinato di interferenza e diffrazione è quello originariamente realizzato da Thomas Young nel 1801, che consiste nel far passare la luce attraverso due fenditure di larghezza d separate da una distanza D . Come abbiamo visto, ciascuna delle due fenditure dà origine per diffrazione a un fascio di luce di apertura \( θ∼λ/d \). Nella regione in cui i due fasci si sovrappongono essi interferiscono, dando origine su uno schermo ad una serie di frange spaziate di
\( \Delta x∼zλ/D \)
che quindi permettono, una volta nota la distanza z dello schermo dalle fenditure, di ottenere la lunghezza d’onda della luce utilizzata.
Un reticolo di diffrazione è una sorta di “generalizzazione” dell’esperimento di Young, nel quale si hanno un grandissimo numero di fenditure ravvicinate, tipicamente dell’ordine delle centinaia per millimetro. In questo caso la figura che si genera è costituita da massimi d’interferenza che si trovano nelle posizioni \( x_m∼±m\frac{zλ}D \), dove m è un intero, rispetto al picco centrale.
9. Dalle dispersione allo spettro delle onde elettromagnetiche
Finora ci siamo limitati ad affermare che le onde luminose hanno una lunghezza d’onda dell’ordine della frazione di μm, ed il cui valore determina il colore che percepiamo. Ora però è il caso di approfondire la questione ricordando uno dei più antichi, famosi e affascinanti esperimenti con la luce, quello compiuto da Newton nel 1666 consistente nella scomposizione della luce bianca nelle sue componenti cromatiche per mezzo di un prisma, e soprattutto della ricomposizione di tale spettro di colori in un singolo fascio di luce bianca grazie ad un secondo prisma.
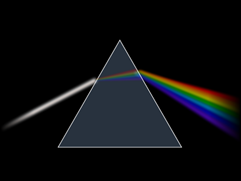
La ragione per cui un prisma scompone la luce nei singoli colori è dovuta al fenomeno della dispersione, ossia al fatto che, come abbiamo già accennato, l’indice di rifrazione di un materiale dipende in realtà dalla lunghezza d’onda, e per essere precisi cresce al decrescere di \( \lambda \) (questa dipendenza è particolarmente accentuata per il tipo di vetro con cui vengono realizzati i prismi). Per la legge di Snell, pertanto, quando un fascio di luce bianca incontra l’interfaccia tra aria e vetro, ciascun colore viene rifratto con un diverso angolo, “piegando” tanto più verso la perpendicolare all’interfaccia quanto minore è la sua lunghezza d’onda. Lo stesso fenomeno si verifica poi all’interfaccia di uscita dal prisma. Il rosso subisce quindi la deviazione minima, mentre la maggiore è subita dal violetto. Se a questo punto si fa entrare questo “arcobaleno” di colori in un prisma capovolto rispetto al primo, si ricompone il fascio originario di luce bianca.
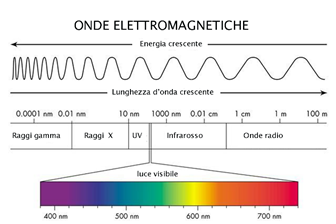
In realtà la luce visibile rappresenta una piccola parte di quelle che in generale si chiamano onde elettromagnetiche e che comprendono radiazioni che vanno dai raggi gamma emessi nelle reazioni nucleari fino alle onde radio, il cui spettro di lunghezze d’onda (nel vuoto) è rappresentato nella figura qui sopra. A radiazioni di lunghezza d’onda minore è associata un’energia maggiore, perché quest’ultima è proporzionale alla frequenza.
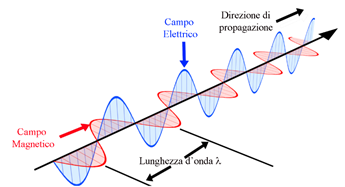
Le onde elettromagnetiche, predette dalla teoria di Maxwell dei fenomeni elettrici e magnetici che generalizza ed estende i concetti elementari introdotti nella Lezione 7, sono onde trasverse, ossia sono costituite da campi elettrici e magnetici che oscillano nel tempo lungo una direzione perpendicolare a quella di propagazione, e possono essere polarizzate, ossia il campo elettrico può oscillare lungo una specifica direzione ortogonale a quella di propagazione (il campo magnetico oscilla sempre perpendicolarmente a quello elettrico), come in figura. In genere la luce ambiente è la sovrapposizione di onde che vibrano in tutte le direzioni, quindi non ha una polarizzazione specifica: tuttavia esistono poi materiali particolari, detti birifrangenti, che permettono di selezionare una particolare direzione di polarizzazione, cosa di grande interesse per molte applicazioni ottiche.