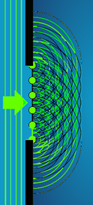
7. Interferenza
Per “sommare” i contributi delle sorgenti secondarie introdotte dal principio di Huygens in modo da ottenere correttamente l’ampiezza e l’intensità dell’onda risultante, dobbiamo tenere conto del fatto che le onde interferiscono. Come abbiamo visto nella quarta lezione, infatti, se sovrapponiamo due onde di uguale ampiezza \( A \) che oscillano sinusoidalmente alla stessa frequenza angolare \( ω=2πν=2πc/λ \) e con lo stesso vettore d’onda \( k=\frac{2π} \lambda \), ma con fasi (ossia l’argomento del seno) che differiscono di \( φ \) l’ampiezza risultante non è in generale \( 2A \), ma è determinata anche dalla loro fase relativa. Infatti, dalla formula generale \( sen(p)+sen(q)=2cos(\dfrac {p-q}2) sen(\dfrac {p+q}2) \) abbiamo:
\( y_1+y_2=Asen(kx- \omega t) +Asen(kx- \omega t+φ)=2Acos(\fracφ2)sen(kx-ωt+\fracφ2) , \)
per cui l’ampiezza risultante è pari a \( 2A \) solo se \( φ=0 \), ossia se le due onde sono “in fase”, ma può essere addirittura nulla se \( φ=π \), ossia se le due onde sono “in opposizione di fase”.
Se poi ricordiamo che l’intensità di un’onda, ossia la sua potenza per unità di superficie, è proporzionale al quadrato dell’ampiezza, vediamo che l’intensità dell’onda risultante varia tra 0 e quattro volte quella di ciascuna delle due onde.