Il fissaidee

Nello spazio tridimensionale la posizione \( \vec{s} \) di un punto \( \textbf{P} \) non può essere definita da un unico numero: oltre alla distanza di \( \textbf{P} \) dall’origine degli assi, dovremo specificare la direzione e il verso che lo caratterizzano. Le grandezze di questo tipo (oltre a posizione anche ad esempio velocità e accelerazione, che ne derivano) sono dette vettori.

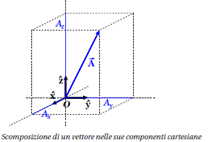
Una qualunque quantità \( \vec{A} \), dotata di orientamento e lunghezza può essere identificata attraverso le sue tre componenti \( \textbf{A}_x;\textbf{A}_y;\textbf{A}_z \)  lungo le tre direzioni cartesiane

  \( \vec{A} = A_x \hat{x} + A_y \hat{y} + A_z \hat{z} \)

Le definizioni di velocità ed accelerazione, media ed istantanea devono essere quindi generalizzate per tenere conto della natura vettoriale di queste grandezze:

\( \vec{v} _{[t_1,t_2]}≡ \frac{\vec{s}(t_2)- \vec{s}(t_1)}{t_2-t_1} \)
\( \vec{a} _{[t_1,t_2]}≡ \frac{\vec{v}(t_2)- \vec{v}(t_1)}{t_2-t_1} \)

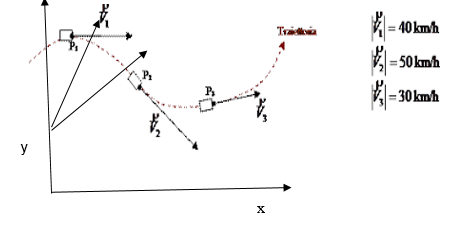
La velocità istantanea risulta sempre tangente alla traiettoria percorsa dall’oggetto.

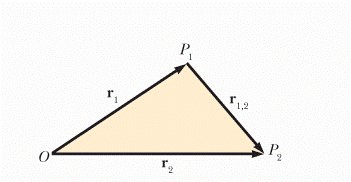
Moto relativo: Dati 2 punti \( \textbf{P_1} \) e \( \textbf{P_2} \) possiamo definire la posizione di \( \textbf{P_1} \) rispetto a \( \textbf{P_2} \) usando la differenza fra i vettori come mostrato nella figura:

Velocità ed accelerazione relative si definiscono allo stesso modo come differenza rispettivamente delle velocità ed accelerazioni.