Il fissaidee

La situazione di un corpo presa in considerazione per il primo principio (nessuna forza agente, oppure sul corpo agiscono solo forze la cui risultante è nulla) è decisamente rara. Nella pratica è di estremo interesse sapere come si comporta un corpo quando non è nelle condizioni per cui vale il principio di inerzia. Questo ce lo dice il secondo principio della dinamica, il quale afferma che un corpo sottoposto a una o più forze si muove con un’accelerazione, il cui modulo è proporzionale al modulo della risultante delle forze e la cui direzione e verso coincidono con quelli della suddetta risultante. In formula possiamo scrivere:

\( \vec{a} \propto \vec{F}_{ris} \)

Dove il simbolo “∝” si legge “è proporzionale a”. Come sai, la proporzionalità (diretta) equivale a dire che una grandezza è uguale all’altra moltiplicata per una costante. In questo caso la costante, determinata sperimentalmente, è il reciproco della massa del corpo, per cui il secondo principio si può scrive:

\( \vec{a} = \frac{1}{\textbf{m}} \vec{F}_{ris} \)

Questo modo di scriverlo evidenzia il ruolo della massa come ciò che “ostacola” l’accelerazione (e perciò è detta “inerziale”): a parità di forza, maggiore è la massa, minore è l’accelerazione. Una forma più familiare per il secondo principio è la seguente:

\( \vec{F}_{ris} = {\textbf{m}} \vec{a} \)

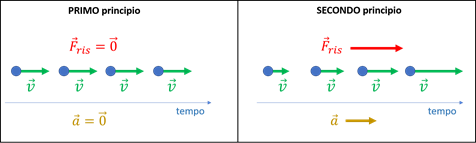
Lo schema seguente può esserti utile per ricordare e mettere in relazione tra loro primo e secondo principio: