Il fissaidee

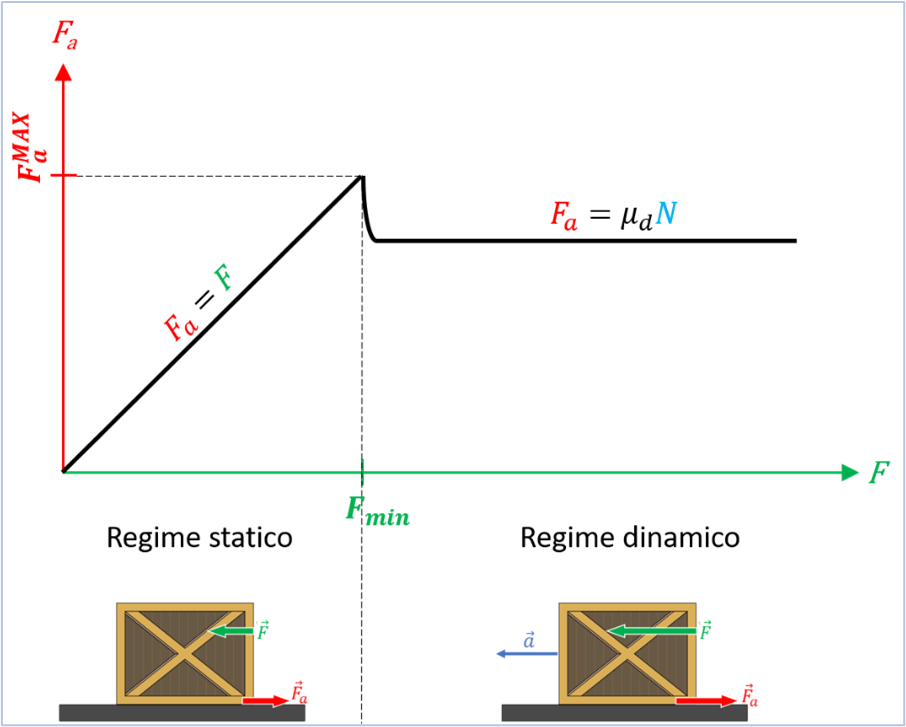
Gli esperimenti mostrano che la scatola non si muove finché il modulo della forza applicata non supera un certo valore minimo \( F_{min} \). Se invece \( F>F_{min} \) la scatola si muove, ma il suo moto è comunque ostacolato dal contatto col pavimento.
Questa situazione è illustrata in dettaglio nella figura a fianco. In particolare, nel “Regime statico”, via via che la forza applicata \( \vec{F} \) aumenta in modulo, aumenta anche la forza orizzontale tra pavimento e scatola \( \vec{F}_a \) (che chiameremo in questo caso di attrito statico), mantenendosi pari in modulo alla forza applicata, cosicché la risultante è nulla e la scatola rimane in equilibrio statico. Esiste però un valore massimo che può assumere la forza di attrito statico (\( \vec{F}_a^{MAX} \)) per cui, allorché la forza applicata supera tale valore, la scatola comincia a muoversi e nel contempo la forza di attrito si stabilizza su un valore leggermente inferiore a \( \vec{F}_a^{MAX} \): il moto entra quindi nel “Regime dinamico”.
Gli esperimenti mostrano anche che sia il valore \( \vec{F}_a^{MAX} \) del massimo attrito statico, che quello \( \vec{F}_a \) dell’attrito dinamico, dipendono solo dalla natura delle superfici in contatto e dalla forza con cui queste sono “pressate” l’una sull’altra, cioè dalla forza normale \( F_N \) (vedi la prima figura di questa sezione), il cui modulo è pari a quello del peso della scatola se il pavimento è orizzontale. In particolare si trova che \( F_a^{MAX}=μ_s F_N \) e \(F_a=μ_d F_N \). Le due quantità adimensionali \( μ_s \) e \( μ_d \), dette rispettivamente coefficiente di attrito statico e coefficiente di attrito dinamico, dipendono esclusivamente dalla natura delle superfici in contatto e soddisfano alla relazione \( 0<μ_d<μ_s<1 \).