Il fissaidee

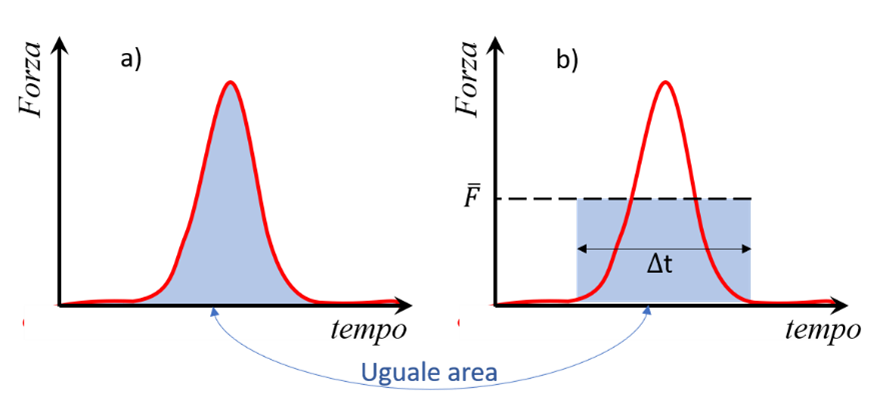
In pratica sono molto frequenti i casi in cui la forza agente sul corpo non è costante. Tra questi, particolare rilievo è assunto dalle forze cosiddette “impulsive”, cioè quelle che agiscono per un intervallo di tempo molto breve ma con intensità elevata: pensiamo ad esempio alla forza agente su una palla da tennis durante l’impatto con la racchetta, oppure su una palla da calcio che venga calciata. Un andamento temporale tipico di forze del genere è mostrato nella parte a) della figura. In questi casi è molto difficile descrivere come la forza varia nel tempo, data l’estrema rapidità del fenomeno; tuttavia a fini pratici è sufficiente conoscere il valore medio del modulo della forza (indichiamolo col simbolo \( \overline{F} \)) nell’intervallo di tempo \( \Delta t \) durante il quale essa agisce. Con riferimento alla figura, \( \overline{F} \) è definita come il valore della forza per cui l’area del rettangolo colorato nella parte b) è uguale all’area sotto il grafico Forza/tempo nella parte a). In questo contesto è utile introdurre una nuova grandezza associata alla forza, detta impulso (simbolo \( I \)), che tiene conto di quanto essa è intensa e di quanto a lungo agisce: \( I \) = “area compresa sotto il grafico forza/tempo” (area colorata nella parte a della figura). Ricordando la definizione di valor medio della forza, l’impulso (che è una grandezza vettoriale avente la medesima direzione e verso della forza) può essere espresso in modulo come  \( I=\overline{F} \Delta t \). 

L’introduzione del concetto di impulso permette di esprimere in maniera generale la relazione tra la variazione della quantità di moto del corpo e le caratteristiche della forza che provoca tale variazione, mediante una legge nota come teorema dell’impulso, la quale afferma che la variazione della quantità di moto di un corpo è uguale all’impulso della forza che agisce su di esso: \( \Delta \vec{p} =\vec{I} \). 

Tutte le precedenti considerazioni, fatte per il caso di una sola forza agente, rimangono valide nel caso in cui sul corpo agiscano contemporaneamente più forze, purché si consideri la forza risultante di queste.