Aggregazione dei criteri
Visualizzare
2. Le unità di misura fondamentali del sistema internazionale (SI)
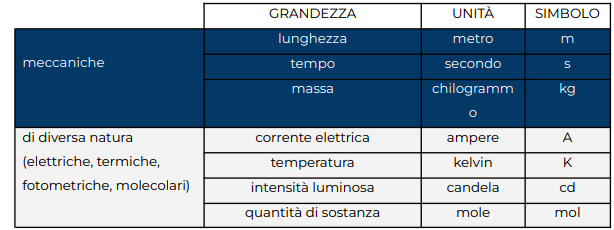
Il Sistema Internazionale (SI) assume sette unità fondamentali, che possono essere combinate in modo da ottenere le unità di misura di ogni altra grandezza fisica:
DALLE UNITÀ ALLE DIMENSIONI
- Talvolta potrebbe farci comodo utilizzare anche altre unità, più adatte al problema considerato o di uso comune. Ad esempio, è sicuramente più facile misurare la distanza delle stelle in anni-luce piuttosto che in metri, o per un marinaio dare una velocità in nodi, piuttosto che in metri al secondo, o una dieta in calorie piuttosto che in joule.
- Unità di misura diverse che si riferiscono alla stessa grandezza fisica hanno però le stesse dimensioni. Così metro e centimetro sono entrambi una lunghezza, o joule e caloria un’energia. Usare le dimensioni, anziché le specifiche unità, elimina ogni possibile confusione.
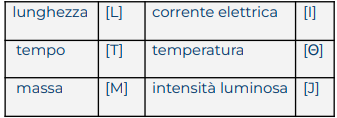
- Le dimensioni di una grandezza fisica si indicano di solito in parentesi quadra, usando questi simboli per le grandezze principali del S.I.
Così ad esempio le dimensioni di una velocità, che è una lunghezza divisa per un tempo,
si indicano con \( [\textbf{V}]=[\textbf{L}]/[\textbf{T}] \) o ancora meglio \( [\textbf{V}]=[\textbf{L}][\textbf{T}]^{-1} \).
N.B. la “quantità di sostanza” è un numero puro, cioè è adimensionale (numero di
moli o di molecole) quindi introdurre un simbolo per essa è poco utile e fuorviante.
si indicano con \( [\textbf{V}]=[\textbf{L}]/[\textbf{T}] \) o ancora meglio \( [\textbf{V}]=[\textbf{L}][\textbf{T}]^{-1} \).
N.B. la “quantità di sostanza” è un numero puro, cioè è adimensionale (numero di
moli o di molecole) quindi introdurre un simbolo per essa è poco utile e fuorviante.
- Al termine di un problema è estremamente utile fare un check delle dimensioni. Ad esempio, di aver calcolato l’energia di un corpo come \( E = f(x,t) \), dove \( f(x,t) \) è una funzione della posizione \( x \) e del tempo \( t \). Allora, poiché un’energia è dimensionalmente una massa per una velocità al quadrato, è essenziale che anche le dimensioni di \( f(x,t) \) siano \( [f] = [\textbf{M}][\textbf{L}]^{2}[\textbf{T}]^{-2} \). Altrimenti, abbiamo sbagliato di sicuro!
