Il fissaidee

Spesso si può capire da quali grandezze dipenda una certa quantità fisica Q, nonché su come ciascuna di queste grandezze entri nell’espressione per Q, combinandole nell’unico modo in cui diano le dimensioni corrette per Q. 

Un esempio? il periodo di oscillazione τ di un pendolo, che ha le dimensioni di un tempo, dipenderà sicuramente dalla sua lunghezza \( l \), dall’accelerazione di gravità \( g \), ed in linea di principio anche dalla sua massa \( \textbf{m} \). Ma per ottenere un tempo dovremmo in qualche modo “far sparire” la massa, che né le dimensioni \( l \) di né quelle di \( g \) contengono. Quindi il periodo non può dipendere da m. L’unica combinazione possibile delle rimanenti grandezze che dia un tempo è la radice di l su \( g \): \( \left[(l/g)^{1/2}\right]=\textbf{L}^{1/2}x\left[\textbf{LT}^{-2}\right]^{-1/2}=\left[\textbf{T}\right]. \)
Quindi il periodo deve potersi scrivere come \( \tau= C\sqrt{\frac{l}{g}} \) dove \( C \) è una costante adimensionale, ossia un numero puro.

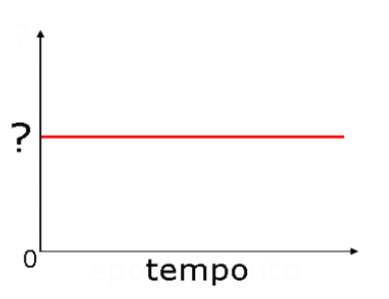
• No labels, no physics! Un grafico dove non vengano indicate le grandezze fisiche rappresentate sugli assi non serve assolutamente a nulla! Ad esempio, nel grafico a fianco, che vorrebbe descrivere il moto di un corpo lungo una retta: 

• se ? = spostamento, il corpo se ne sta fermo
• se ? = velocità  il corpo si muove di moto rettilineo uniforme
• se ? = accelerazione  il corpo si muove di moto uniformemente accelerato

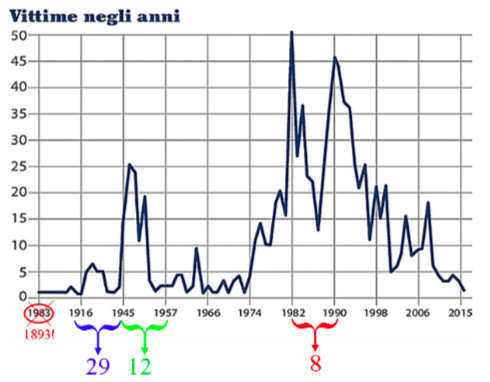
• Assi sì, ma fatti bene! Spesso (soprattutto nell’infografica dei giornali) si trovano grafici che lasciano a dir poco perplessi, soprattutto perché gli assi sono disegnati in modo a dir poco “creativo”…guardate ad esempio questo grafico, tratto da uno dei maggiori quotidiani italiani, che vorrebbe rappresentare i decessi provocati nel tempo dalla mafia. A parte il banale refuso per il primo anno, che è ovviamente il 1893, intervalli uguali sull’asse delle ascisse rappresentano spesso un numero di anni molto diverso. Ciò, oltre che sbagliato, è davvero fuorviante!

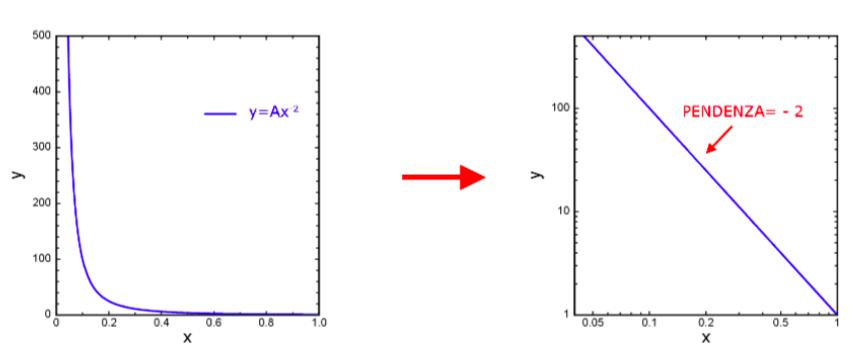
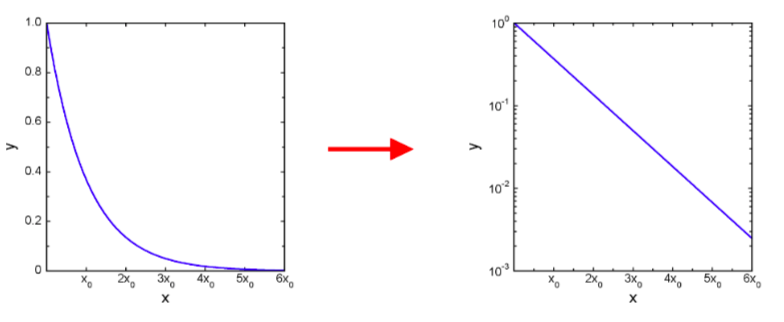
• Gli assi logaritmici. Quando una grandezza fisica ha un comportamento particolare, può essere comodo rappresentarla utilizzando, anziché degli assi lineari, assi con una spaziatura logaritmica dell’ascisse, o dell’ordinate, o di entrambe. Ad esempio:
• andamento esponenziale: \( y=exp (-x/x_{0} ) \)

• andamento a legge di potenza: \( y=Ax^{c} \)