Il fissaidee
Aggregazione dei criteri
Visualizzare
4. Statistica: il minimo essenziale
Distribuzioni di una grandezza statistica. Molte grandezze non hanno UN valore ben determinato, ma piuttosto possono assumere una serie di valori diversi entro un certo intervallo. Indichiamo con \( \textbf{K} \) una grandezza di questo tipo e con\( k \) un generico valore tra quelli che essa può assumere (che possono essere anche infiniti!). Se ora raccogliamo un campione statistico costituito da \( N \) risultati di una misura della variabile ed indichiamo con \( n_{k} \) il numero di volte che si ottiene il valore \( k \), possiamo definire le frequenze relative \( f_{k}=\frac{n_{k}}{N} \) Un grafico delle \( f_{k} \) verso \( k \) viene detto distribuzione statistica. Ovviamente la somma delle frequenze relative è pari ad uno, perché \( \Sigma _{k}n_{k}= N \)
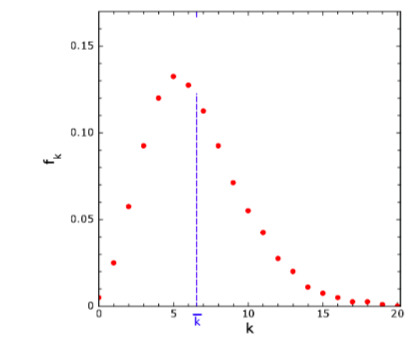
La figura a fianco mostra ad esempio la distribuzione delle frequenze relative per il numero di risposte esatte, su un totale di 20 domande, nella sezione “Scienze” di un test CISIA per l’ammissione alle facoltà di Ingegneria svoltosi nel 2008.
La figura a fianco mostra ad esempio la distribuzione delle frequenze relative per il numero di risposte esatte, su un totale di 20 domande, nella sezione “Scienze” di un test CISIA per l’ammissione alle facoltà di Ingegneria svoltosi nel 2008.
- Media e deviazione standard. Il valor medio k, che ci dà una stima del “valore tipico” della variabile k, può essere semplicemente definito come la somma di tutti i risultati divisa per il numero totale di misure, ma un modo alternativo e sicuramente più utile è quella di pesare ciascun valore con la frequenza con cui viene ottenuto, scrivendo
\( \overline{k}=\sum_k f_{k}k \)
Nella distribuzione mostrata in figura, ad esempio, si ha \( \overline{k} \simeq 6,55 \)(indicata dalla linea blu).
Una stima della larghezza di una distribuzione si può invece ottenere calcolando il valor medio della differenza al quadrato dei valori dalla media e prendendono la radice quadrata, parametro che è detto deviazione standard \( \sigma_{k} \) della variabile \( k \):
\( \sigma_{k}=\sqrt \Sigma _{k}f_{k}(k-\overline{k})^{2} \)
