Il fissaidee

L’equazione di stato è una relazione termodinamica tra le tre variabili \( P,V,T \) (oppure \( P,ρ,T \)). Se ne fissiamo una, possiamo quindi determinare come variano le altre due l’una in funzione dell’altra. Così un gas potrà ad esempio subire una:

• trasformazione isoterma (a temperatura costante)
• trasformazione isobara (a pressione costante)
• trasformazione isocora (a volume costante)

Si possono poi rappresentare queste trasformazioni su un piano cartesiano scegliendo due delle tre variabili come assi. È spesso utile scegliere \( V \) (come ascissa ) e \( P \) (come ordinata) perché il loro prodotto è dimensionalmente un lavoro. Su un diagramma \( P,V \) una trasformazione isobara ed una isocora sono quindi semplicemente due rette parallele rispettivamente all’asse delle ascisse e a quello delle ordinate, mentre le trasformazioni isoterme sono iperbole equilatere come quelle mostrate nel disegno. Ogni punto del piano corrisponde a uno stato del gas definito dai valori di \( P,V \) e dalla temperatura corrispondente all’isoterma (unica!) che passa per quel punto.

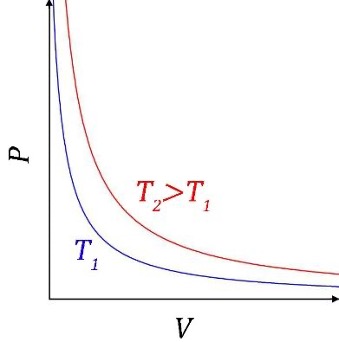
Possiamo però pensare anche a dei cambiamenti di stato in cui nessuna delle tre variabili è costante, ma \( P, V, \) e \( T \) sono comunque legate da una precisa relazione. Ad esempio, possiamo pensare ad una trasformazione in cui il gas non riceve né cede calore, che si dice adiabatica. Sul diagramma \( P,V \) l’equazione di un’adiabatica è 

\( PV^ \gamma =costante \)

dove \( \gamma \) è un esponente che dipende dal tipo di gas, ed in particolare da quanti atomi formano una molecola, ma che è in ogni caso maggiore di uno (per gas monoatomici \( \gamma \)=5/3).  Il pannello A nella figura a fianco mostra il confronto con un’isoterma. 

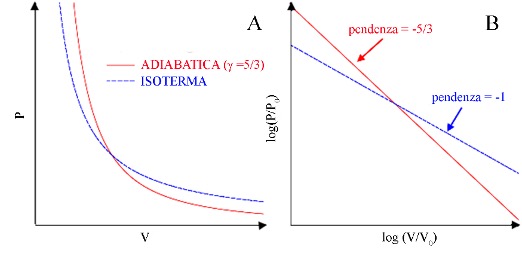
Notiamo che sia l’isoterma che l’adiabatica sono delle leggi di potenza, quindi, come mostrato nel pannello B, sono delle rette su un grafico bilogaritmico (\( V_0 \) e \( P_0 \) sono due costanti con le dimensioni di un volume e di una pressione introdotte per rendere adimensionali i logaritmi).  

Dato che in una trasformazione adiabatica non si scambia calore, se questa viene compiuta molto lentamente, in modo da essere reversibile, non varia neppure l’entropia. Quindi un’adiabatica reversibile è anche una trasformazione isoentropica.