Il fissaidee

Il parametro che quantifica l’efficienza di una macchina termica è il rendimento , definito come il rapporto tra il lavoro compiuto in un ciclo dalla macchina ed il calore da essa assorbito:

\( η=\frac{|W|}{|Q_c|}=1-\frac{|Q_f|}{|Q_c|} \)

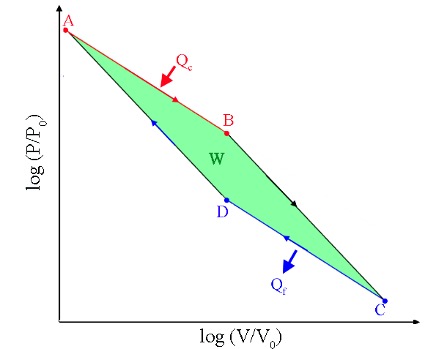
Come conseguenza del Secondo Principio,  \( η<1 \), ma il rendimento di una macchina termica ha in realtà un limite superiore che fu stabilito da Sadi Carnot, un ingegnere francese, fin dal 1824. Carnot stabilì che per ottenere il massimo rendimento, una macchina deve utilizzare il minimo numero possibile di sorgenti termiche, cioè due (una calda ed una fredda) e compiere un ciclo formato da quattro trasformazioni, due isoterme e due adiabatiche. Nella prima isoterma il gas viene fatto espandere a contatto  con la sorgente calda, poi viene ulteriormente espanso, ma adiabaticamente, fino alla temperatura della sorgente fredda, quindi viene compresso a contatto con la  sorgente fredda, ed infine viene ulteriormente compresso adiabaticamente fino a ritornare alla stato di partenza (si veda la figura qui sotto, dove il ciclo di Carnot è rappresentato in un diagramma log-log). 

Il rendimento è massimo solo se ognuna delle trasformazione è “quasi” reversibile, ossia se la temperatura della macchina differisce di pochissimo da quella delle sorgenti con cui viene messa a contatto, e se le trasformazioni adiabatiche avvengono molto lentamente. In questo caso \( η \) dipende solo dal rapporto \( \dfrac{|Q_f |}{|Q_c |} \). 

Successivamente Kelvin e Joule mostrarono che nel ciclo di Carnot ideale il rapporto tra i calori scambiati con le due sorgenti può essere scritto semplicemente come rapporto delle temperature delle due sorgenti, purché queste vengano misurate proprio su quella scala “assoluta” che aveva avuto origine dallo studio delle leggi dei gas. Ovverosia, misurando le temperature in kelvin, si ha:

\( η=1-\dfrac {T_f}{T_c} \)