Il fissaidee

Introduciamo ora un concetto molto utile, quello di campo elettrico. Supponiamo di essere in presenza di diverse cariche che interagiscono fra di loro tramite le forze di Coulomb: in ogni punto \( r \) dello spazio potremo esplorare l’effetto dell’intera distribuzione di cariche collocando in quel punto una carica \( q \) abbastanza piccola da non modificare la distribuzione spaziale delle cariche stesse. Detta \( \textbf{F}(r) \) la forza di Coulomb agente su questa “carica di prova” chiameremo campo elettrico nel punto \( r \) il vettore

\( E(r)=\dfrac{F(r)}{q} \)

che ci permette di valutare la forza che agisce su una qualsiasi carica elettrica collocata nello spazio. Si può rendere visivamente l’andamento del campo in ogni punto, tracciando le linee di campo la cui direzione e verso corrispondono a quella della forza agente su di una carica positiva posta nel punto considerato.

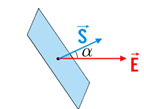
Possiamo quantificare quanto si “addensino” nello spazio le linee di campo per mezzo del concetto di flusso del campo elettrico attraverso una superficie. Consideriamo un campo \( E \) costante e una superficie piana che rappresenteremo come un vettore \( S= Sn \) orientato secondo la normale \( n \) alla superficie, e definiamo il flusso \( \Phi_S ( E ) \) del campo \( E \) attraverso \( S \) come il prodotto scalare di \( E \) con \( S \):

\( \Phi _S(E)=E⋅S=ES\,cos\,\, \alpha \)

Il concetto di flusso può essere applicato a qualsiasi vettore, non solo al campo elettrico. Per il campo elettrico, che è proporzionale a \( \dfrac1{r^2} \), si può però dimostrare (teorema di Gauss) che il flusso attraverso una qualsiasi superficie chiusa è dato semplicemente dalla somma algebrica delle cariche che si trovano all’interno della superficie, divisa per la costante dielettrica:

\( \Phi _S(E)= \dfrac{ \sum{q_i} }{ \epsilon_0 } \)

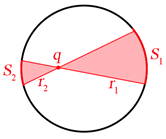
La ragione di fondo per cui il flusso dipende solo dalla carica totale e non da dove si trovano le singole cariche è che il campo elettrico decresce con il quadrato della distanza dalle cariche che lo generano. È facile intuirlo se consideriamo una singola carica all’interno di una sfera come nella figura a fianco: il campo su \(S_1 \)è infatti ridotto rispetto a quello su \( S_2 \) di un fattore  \( (\dfrac{r_2}{r_1} )^2 \), ma d’altronde l’area di \( S_1 \) è a sua volta più grande di quella di \( S_2 \)  di un fattore \( (\dfrac{r_1}{r_2} )^2 \), per cui il flusso attraverso le due superfici è lo stesso dovunque si trovi \( q \). 

Utilizzando il teorema di Gauss si può facilmente calcolare il campo elettrico per distribuzioni di carica che presentino simmetrie. Ad esempio, a distanza r da un filo infinitamente lungo con densità di carica per unità di lunghezza si trova che l’intensità del campo elettrico vale \( E= \dfrac{\lambda }{2 \pi \epsilon_0r } \), mentre nelle vicinanze di una superficie piana con densità di carica \( \lambda \) per unità di superficie l’intensità del campo elettrico vale \( E= \dfrac{ \sigma }{2 \pi \epsilon_0 } \).

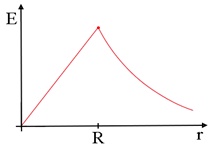
Una distribuzione sferica di carica di raggio \( R \) genera al suo esterno un campo elettrico identico a quello che sarebbe generato se tutta la carica fosse concentrata al centro della sfera, mentre all’interno il campo cresce linearmente con la distanza r dal centro, come in figura.