Il fissaidee

Per determinare la condizione di affondamento abbiamo considerato il caso in cui il corpo è totalmente immerso nel liquido e quindi \( V_{imm}=V \).  Tuttavia, nel regime di galleggiamento, cioè quando \( ρ_c<ρ_L \), il corpo è solo parzialmente immerso. In tal caso è utile chiedersi quale sia la frazione del volume del corpo che risulta immersa, cioè il valore del rapporto \( V_{imm}/V \) Possiamo determinarla considerando le grandezze illustrate nella figura.

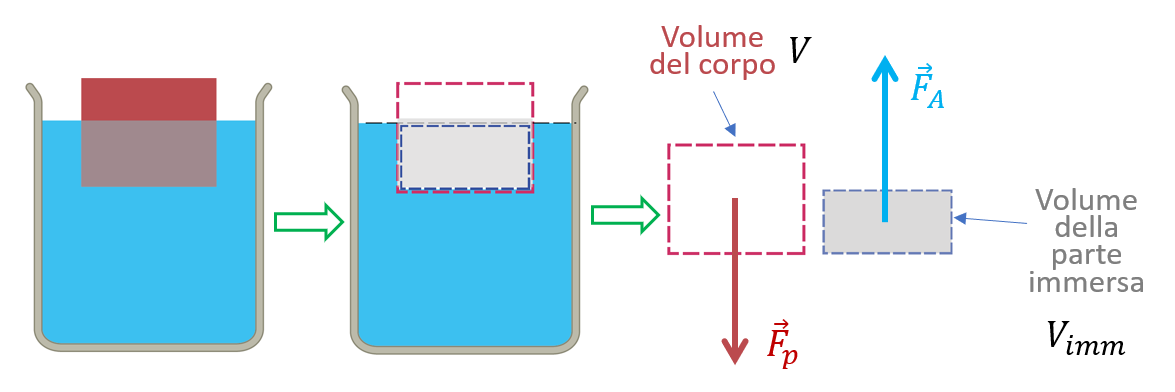
In questo caso la condizione di equilibrio \( F_p=F_A \)si esprime come \( ρ_c g=V_{imm}  ρ_L g \)Da qui, semplificando l’accelerazione di gravità otteniamo \( V_{imm}/V=ρ_c/ρ_L \). Quindi la frazione di volume del corpo che risulta immersa è pari al rapporto tra la densità del corpo e quella del liquido. Questo fatto è particolarmente significativo nel caso in cui il corpo è costituito di ghiaccio e il liquido è l’acqua. Conosci il modo di dire “… è solo la punta dell’iceberg"? Per intendere che ciò che appare è solo una minima parte della realtà intera? Ebbene, vedremo ora l’origine fisica di questo modo di dire chiedendoci qual è la frazione del volume di un iceberg che emerge dall’acqua. La risposta la possiamo ottenere ricordando che la densità del ghiaccio è \( ρ_c=0{,}92 g/cm^3, \) mentre quella dell’acqua è \( ρ_L=1 g/cm^3 \). Sostituendo tali valori nella formula ricavata prima otteniamo\( V_{imm}/V=0{,}92 \). In termini percentuali questo significa che il 92% dell’iceberg è immerso e quindi la parte che si vede è solo l’8% circa! In realtà il conto che abbiamo fatto sottostima un po’ la percentuale emersa, in quanto non abbiamo tenuto conto che l’iceberg è fatto di acqua dolce, mentre l’acqua in cui galleggia è salata. Poiché quest’ultima ha una densità un po’ maggiore di \( 1 g/cm^3 \) (dipende dal mare considerato, ma mediamente è \( ρ_L=1{,}02 g/cm^3 \) si ottiene una percentuale emersa intorno al 10%; in ogni caso questo non inficia il modo di dire!