Il fissaidee

La visione pienamente quantistica dell’atomo ci porta ad abbandonare alcuni concetti classici ai quali siamo profondamente affezionati, fra i quali il fatto che una particella puntiforme possa essere sempre ben localizzata nello spazio e quello, connesso al precedente, che ci porta a pensare che una particella in moto percorra un’orbita ben definita, descritta da un ente geometrico familiare quale una circonferenza o un’ellisse. Infatti, laddove la fisica classica descrive le particelle per mezzo di variabili che assumono valori ben definiti (posizione e velocità), nel quadro quantistico ciascuna particella è descritta da un oggetto matematico detto funzione d’onda, che racchiude tutta l’informazione che è possibile ottenere sperimentalmente sulla situazione della particella. Tale funzione (i cui valori, per inciso, sono numeri complessi) descrive lo stato quantistico di una particella da vari punti di vista. Quello forse intuitivamente più vicino al concetto classico di particella è il seguente: il valore medio del modulo della funzione d’onda in una piccola regione di spazio, moltiplicato per il volume di tale regione, fornisce la probabilità che effettuando una misura la particella venga ivi trovata. Questo carattere probabilistico (in contrapposizione a quello deterministico della fisica classica) è onnipresente nella descrizione quantistica degli oggetti fisici.

Nel quadro descritto, il concetto di orbita presente nei primi modelli atomici (anche in quello di Bohr) viene sostituito da quello di “orbitale”. Certamente ti saranno familiari le tipiche forme di orbitali mostrate in figura: le diverse forme corrispondono a differenti valori dei numeri quantici \( n \), \( l \) e \( m_l \), mentre \( m_S \) non è legato alla forma dell’orbitale: i due valori che tale numero quantico può assumere fanno sì che in un dato orbitale (individuato da una terna di valori dei restanti tre numeri quantici) possano trovarvisi fino a due elettroni, e in tal caso avranno l’uno \( m_S=-1/2 \) e l’altro \( m_S=+1/2 \): questa condizione è una delle molteplici conseguenze di un importante principio della meccanica quantistica formulato da Wolfgang Pauli, il principio di esclusione.

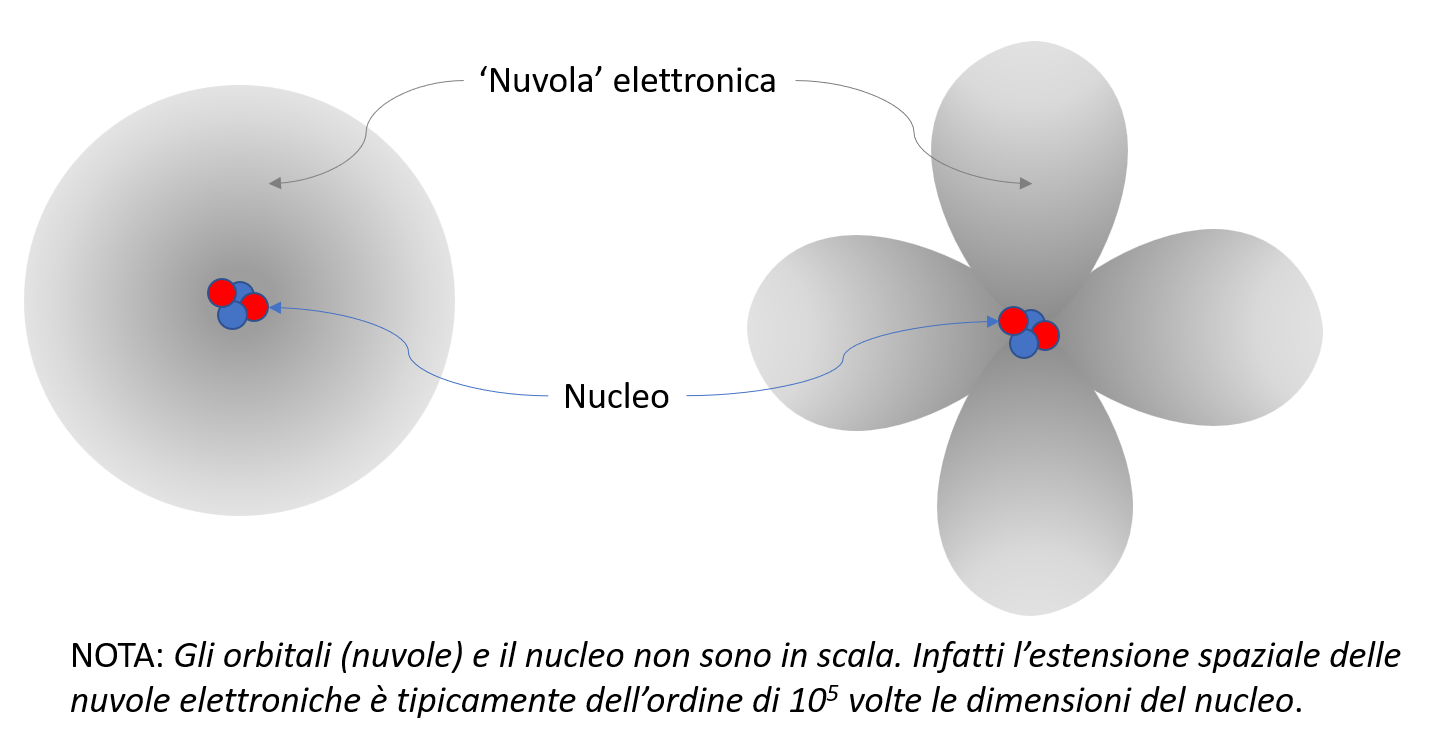
Conviene osservare che il termine “orbitale” è, per motivi storici, evocativo del termine “orbita”; tuttavia l’orbitale NON è da intendere come una sorta di “orbita tridimensionale”, ma rappresenta visivamente la distribuzione spaziale della probabilità che l’elettrone descritto da quell’orbitale si trovi in una certa regione dello spazio: più la nuvoletta è “densa” in quella regione, maggiore è la probabilità di trovarci l’elettrone. In particolare, l’orbitale non è un insieme di orbite molto fitte che si confondono tra loro.