Il fissaidee

Seconda tappa

Nel caso di moto unidimensionale la posizione è data semplicemente dalla coordinata lungo la retta, diciamo \( x \); la funzione \( x(t) \) che descrive la posizione \( x \) in funzione del tempo \( t \), prende il nome di equazione oraria. 

Un’ulteriore grandezza necessaria per descrivere il moto è la velocità: cominciamo col definire la velocità media: si definisce velocità media nell’intervallo di tempo \( [t_1, t_2] \) il rapporto tra lo spazio percorso tra \( t_1 \) e \( t_2 \) (cioè \( x(t_2) – x(t_1) \) )- e l’intervallo di tempo impiegato a percorrerlo \( (t_2 – t_1) \). In formula:

\( v_{t_1,t_2 }≡ \frac{x(t_2 )-x(t_1 )}{t_2-t_1} \)

Se gli intervalli tendono a zero possiamo ora definire la velocità istantanea all’istante di tempo t₁ come la velocità media nell’intervallo di tempo \( [t_1, t_2] \) quando \( t_2 \) si avvicina sempre di più a \( t_1 \) (in linguaggio più matematico quando \( t_2 \) tende a \( t_1 \)). Graficamente, il valore della velocità istantanea sarà dato dal coefficiente angolare della tangente al grafico della legge oraria nell’istante t₁.

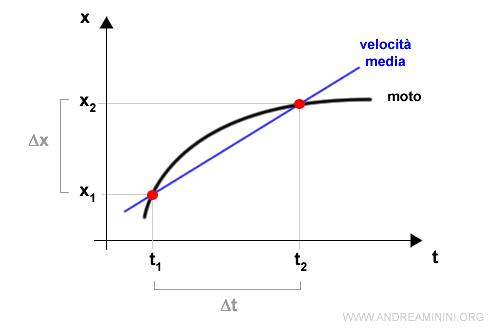
Con una notazione più compatta possiamo ora anche dire che la velocità media è data dal rapporto fra intervalli \( \frac{ \Delta x}{\Delta t} \), mentre quella istantanea dal rapporto degli intervalli infinitesimi \( \frac{dx}{dt} \), identificabile come la derivata di \( x \) rispetto al tempo; viceversa otterremo \( x \) dalla velocità con una operazione di integrazione.

Ad esempio consideriamo un moto con velocità \( v \) costante nel tempo: l’equazione oraria sarà \(x(t) = x0 + v t\)

Per spostarti tra le pagine del fissaidee utilizza le frecce azzurre.