Unit 1: frequenze, distribuzioni di frequenze ed istogrammi
Aggregazione dei criteri
Visualizzare
- Distribuzioni di frequenza per classi
- Istogramma
2. Distribuzione delle frequenze per una variabile
Consideriamo la seguente distribuzione delle frequenze del carattere altezza misurato su un collettivo di 200 studenti raggruppati in 5 classi di eguale ampiezza:
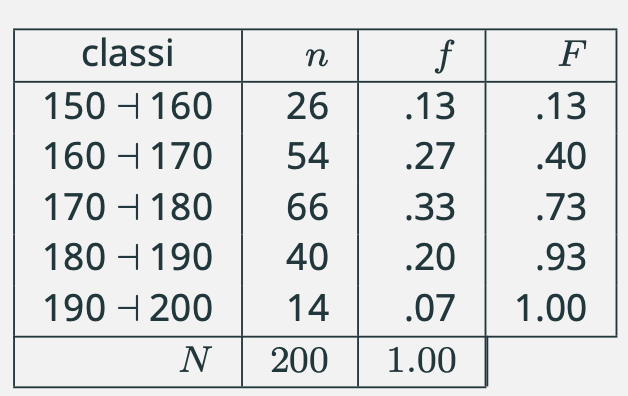
Poiché l’altezza è un carattere continuo, è una variabile, bisogna rappresentare la distribuzione delle frequenze in modo che tutte le modalità comprese fra i limite inferiore della distribuzione (150) e il limite superiore (200) siano comprese
in una (ed una sola) classe.
Il simbolo ⊣, usato per definire una classe, sta a indicare che limite inferiore non è compreso nella classe mentre il limite superiore è compreso. Ovviamente si può utilizzare anche il simbolo ⊢.
Notazione
- frequenza assoluta \(\{n_1, n_2, \cdots, n_k\} \longrightarrow\) numero di unità statistiche che appartengono alla classe
- numerosità del collettivo \(N\)
- frequenza relativa \(\{f_1, f_2, \cdots, f_k\}\longrightarrow\) \(f_i = n_i/N\) per \(i=1,\ldots k\)
- frequenza (relativa) cumulata \(\{F_1, F_2, \cdots, F_k\}\longrightarrow\) \(F_1=f_1, \quad F_2 = f_1 + f_2,\) ecc.
