- Distribuzioni di frequenza per classi
- Istogramma
4. Istogramma - classi di ampiezza diversa
Consideriamo sempre gli stessi dati, ma le ultime due classi \([180 \dashv 190]\) e \([190 \dashv 200]\) sono state raggruppate in un’unica classe \([180 \dashv 200]\).
Raggruppando due classi, o comunque fissando classi di ampiezza differente, non è possibile continuare a utilizzare la frequenza (assoluta o relativa) per determinare l’altezza dei rettangoli. Per preservare il rapporto fra area del rettangolo e frequenza della classe bisogna ricorrere alle intensità (o densità).
La tabella che segue riporta la distribuzione in cui le ultime due classi sono state riunite in un'unica classe.
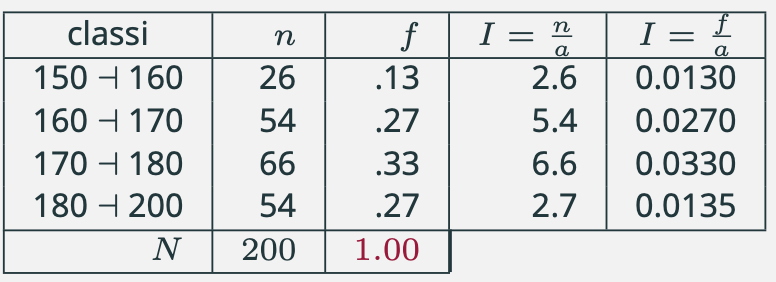
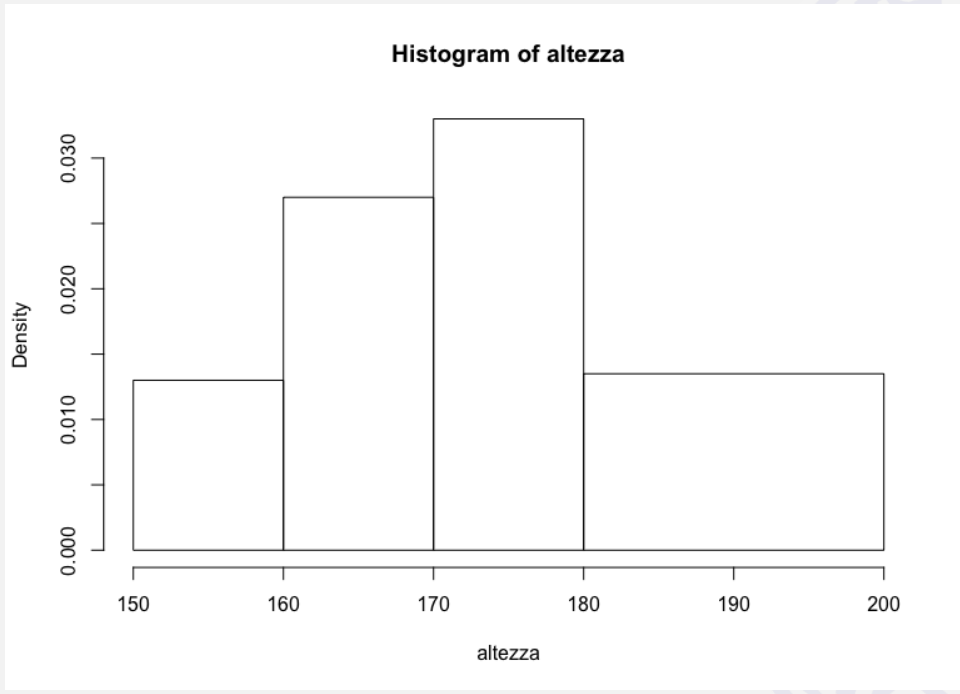
La rappresentazione per mezzo delle intensità (densità) è l’unica possibile se le classi non sono equiampie.
Le intensità si ricavano dalla formula \[I_i = \frac{n_i}{a_i}\], dove \(a_i\) indica l’ampiezza della classe e, per ciascuna classe è calcolata attraverso la differenza fra l’estremo superiore e l’estremo inferiore della classe stessa.
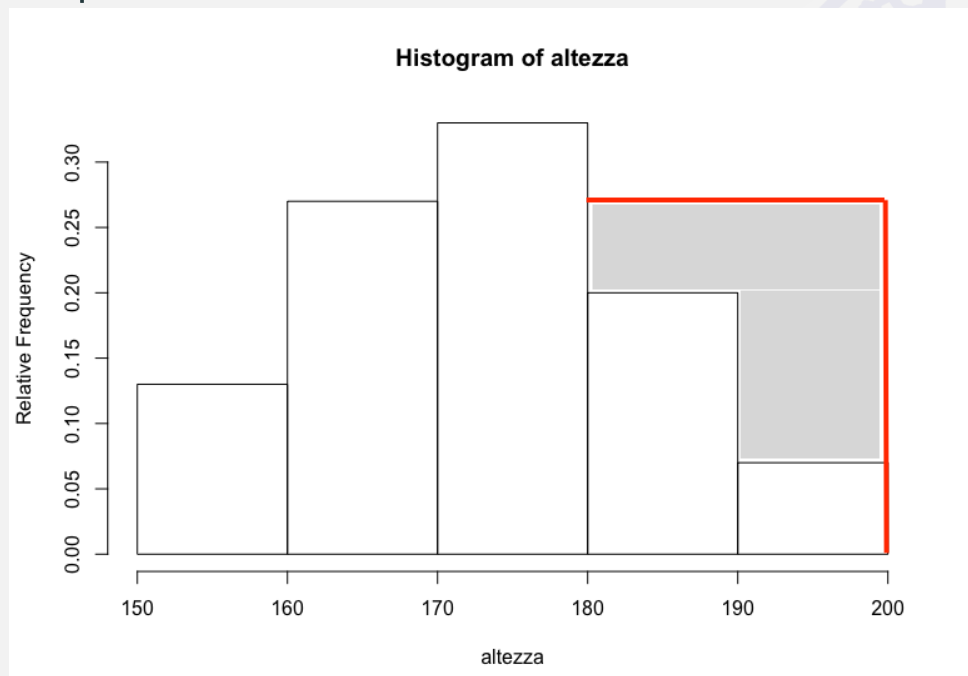
Poiché l'area descritta da ciascun rettangolo e quindi anche l'area totale dell'istogramma devono essere in proporzione alla frequenza che rappresentano e questa proporzione resta costante, se si utilizzasse la frequenza e non l'intensità si avrebbe una rappresentazione come quella riportata di seguito, dove l'area grigia rappresenta un accrescimento ingiustificato dell'area totale. Ingiustificato poiché non corrisponde a un incremento della frequenza, ma solo a una sua diversa distribuzione fra le classi.