Unit 1 - Associazione fra caratteri: definizioni e misure per i caratteri statistici
Aggregazione dei criteri
Visualizzare
40. Analisi della dipendenza: Esempio
 |
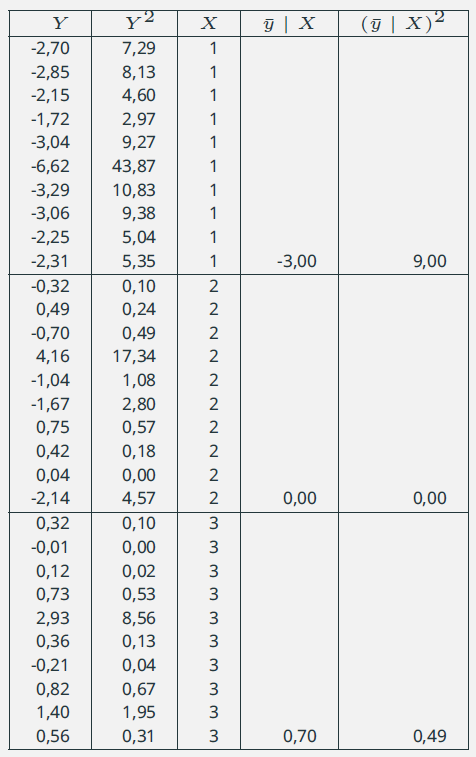Calcolo del coefficiente \(\eta^2\) \({\bar{y}}= \displaystyle{\frac{1}{30}\sum_{i=1}^{30}{y_i} = 0,77}\) \(N{\bar{y}}^2= 30\times 0,587=17,63\) \(\sum{Y^2}=146,41\) \(DEV(Y)= 146,41 - 17,63 = 128,78\) \(DEV_W(Y)=10*((Y\mid X_1)^2 + (Y\mid X_2)^2 +\) \(\qquad \qquad \qquad + (Y\mid X_3)^2) - \sum{Y^2} = 77,27\) \[ \eta^2 = \frac{77,27}{128,78} = 0,6 \]E' possibile linearizzare l'indice usando la radice quadrata \[ \eta = \sqrt{\eta^2} = \sqrt{0,6} = 0,77 \] |
|---|
