Unit 3: indici di posizione (parte 2 di 3)
Aggregazione dei criteri
Visualizzare
- Medie di posizione
- La mediana: definizione, criteri di calcolo e proprietà
- Quartili di una distribuzione
- Quantili di una distribuzione
4. Mediana per dati raggruppati in classi: interpolazione /1
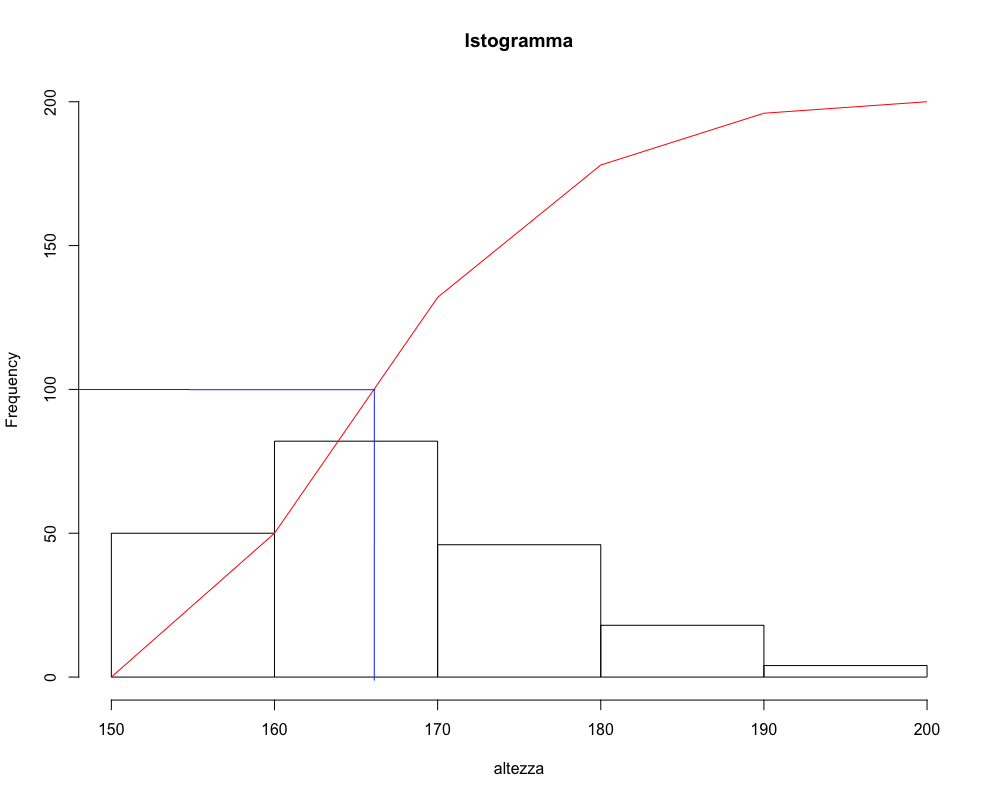
Consideriamo la distribuzione delle frequenze relativa alle altezze che abbiamo già visto in precedenza.
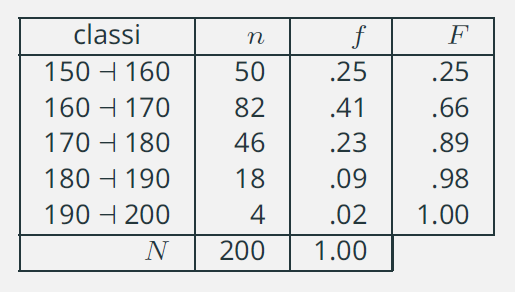
La classe \(160\) a \(170\) rappresenta la classe mediana.
Indichiamo la classe mediana con \(X_{Me}\) e la mediana con \(Me\):
- regola della proporzione:
\[ Me = \inf (X_{Me}) + a_{Me} \dfrac{F(X_{Me}) − F(X_{Me^{-}})}{f(X_{Me})} \]
- la mediana corrisponde alla modalità individuata come il limite inferiore della classe mediana più una frazione dell’ampiezza, proporzionale alla frequenza fra \( F(X) = 0,5 = \dfrac{N}{2} \) meno il retrocumulo e la frequenza della classe mediana.
- - Nell’esempio:
\[ Me = 160 + 10 \dfrac{0,50 − 0,25}{0,41}= 166,1 \]
