Unit 4: indici di posizione (parte 3 di 3)

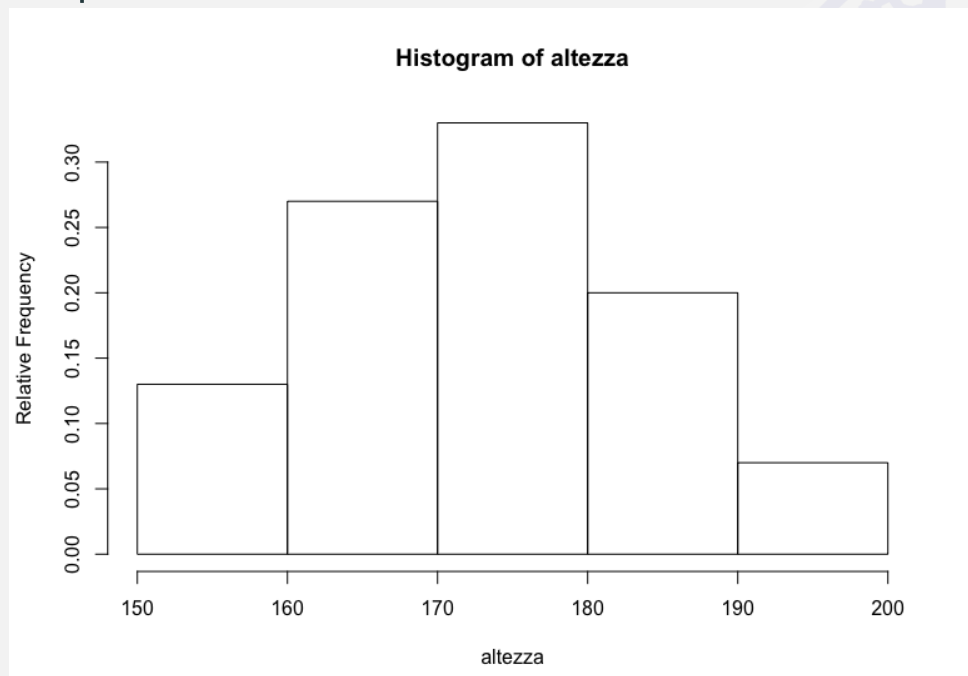
Calcolo della media aritmetica per dati raggruppati in classi. Consideriamo gli stessi dati degli esempi precedenti e il medesimo istogramma che ne descrive la distribuzione.

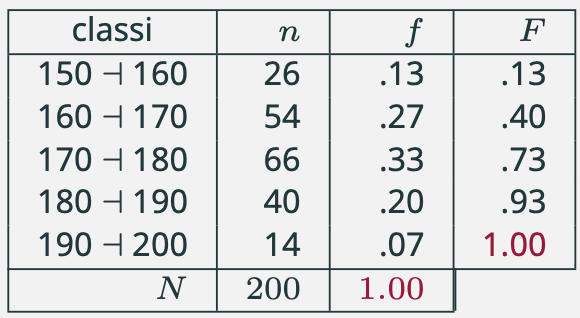
Istogramma e distribuzione delle frequenze assolute e relative per i dati relativi alla variabile altezza.

\([1;2;3]\) la media è 2,0
\(\vdots\)
\([1, \cdots, N]\) la media è \(\frac{1 + N}{2}\)

Se ne deduce, quindi, che la media corrisponde con il valore centrale o centralità se la successione è uniforme. Pertanto, in assenza di altre informazioni, assumiamo che la distribuzione delle osservazioni all'interno di ciascuna classe è una distribuzione uniforme e di conseguenza la media della classe corrisponde al valore centrale.

Se indichiamo con la lettera \(K\) il numero generico di classi e con la lettera \(k\) la generica classe, per cui possiamo scrivere che \(k=1,\ldots K\) (che \(k\) varia fra \(1\) e \(K\)), per la proprietà associativa della media aritmetica, possiamo determinare la media generale \(\bar{x}\) attraverso la media ponderata delle medie parziali di ciascuna classe. Avremo quindi
\[
\boxed{\bar{x} = \frac{\sum_{k=1}^{K}n_k \times c_k }{\sum_{k=1}^{K}n_k}}.
\]

Nell'esempio abbiamo che

\[
\bar{x} = \frac{155\times 26 + 165\times 54 + 175 \times 66 + 185 \times 40 + 195 \times 14 }{26+54+66+40+14} = 173,1.
\]

Naturalmente è possibile utilizzare le frequenze relative al posto delle frequenze assolute. In questo caso l'operazione sarà la seguente e il risultato lo stesso

\[
\bar{x} = 155\times 0,13 + 165\times 0,27 + 175 \times 0,33 + 185 \times 0,20 + 195 \times 0,07 = 173,1.
\]