- Distribuzioni di frequenza per classi
- Istogramma
1. Distribuzione delle frequenze
Quando la numerosità del collettivo diventa grande, le modalità osservate sono troppo numerose perché da una semplice osservazione si possa apprezzare come si è distribuito il carattere all’interno del collettivo.
Tabelle che associano a ciascuna modalità la frequenza corrispondente sono denominate distribuzioni di frequenza.
Nel caso di caratteri quantitativi è necessario, per ottenere la distribuzione di frequenza, creare classi di modalità.
| Classi | n | f | I | ||
|---|---|---|---|---|---|
| 0 | - | 2,0 | 4 | 0,114 | 0,057 |
| 2,0 | - | 2,5 | 6 | 0,171 | 0,343 |
| 2,5 | - | 3,0 | 15 | 0,429 | 0,857 |
| 3,0 | - | 5,0 | 9 | 0,257 | 0,129 |
| 5,0 | - | 8,0 | 1 | 0,029 | 0,010 |
| Totale | 35 | 1,000 | |||
- Per ottenere una distribuzione di frequenza a partire da un carattere continuo è necessario suddividere il campo di variazione del carattere in Classi. Le classi possono essere di eguale ampiezza (tabella a sinistra) o di ampiezza variabile (a destra).
- Per creare le classi è necessario suddividere l’intervallo in cui è definito il carattere in sottointervalli di eguale ampiezza (classi equiampie) o di ampiezza differente.
- Utilizzare classi di ampiezza differente è utile soprattutto nel caso di distribuzioni caratterizzate da forte asimmetria o con forte variabilità verso i valori estremi
- Il simbolo “\(\dashv\) indica che l’estremo inferiore della classe è incluso e l’estremo superiore è escluso.
- Le frequenze assolute, generalmente indicate con \(n\), per ciascuna classe, indicano il numero delle unità statistiche che presentano una modalità appartenente all’intervallo della classe.
La somma di tutte le frequenze assolute corrisponde alla numerosità del collettivo, che generalmente si indica con \(N\). - Le frequenze relative si determinano dividendo le frequenze assolute per il la frequenza totale: \[f = \frac{n}{N}.\]
Il totale delle frequenze relative, naturalmente, è sempre 1. - L’intensità si utilizza per realizzare istogrammi con classi di ampiezza differente e si determina dividendo la frequenza relativa per l’ampiezza della classe: \[I = \frac{f}{{\rm sup}(x) - {\rm inf}(x)}.\]
- Per rappresentare graficamente la distribuzione delle frequenze associate a un carattere continuo o variabile si utilizza l’istogramma.
- L’istogramma è costituito da una serie di rettangoli contigui, che hanno per base l’ampiezza della classe e la superficie proporzionale alla frequenza della classe. Utilizzando questo principio è possibile accorpare due o più classi contigue o definire distribuzioni in classi che hanno ampiezze diverse.
- L’istogramma è una
rappresentazione della distribuzione delle frequenze su un piano
cartesiano (generalmente) l’asse delle ascisse rappresenta il carattere e
le ordinate le altezze dei rettangoli determinate dal rapporto fra
l’area e l’ampiezza della
base.
---------------------------------------------------------------
Ecco due esempi ricavati a partire dalla serie completa della variabile
| Classi | n | f | I | ||
|---|---|---|---|---|---|
| 1,0 | - | 3,0 | 25 | 0,714 | 0,357 |
| 3,0 | - | 5,0 | 9 | 0,257 | 0,129 |
| 5,0 | - | 7,0 | 0 | 0,000 | 0,000 |
| 7,0 | - | 9,0 | 1 | 0,029 | 0,014 |
| Totale | 35 | ||||
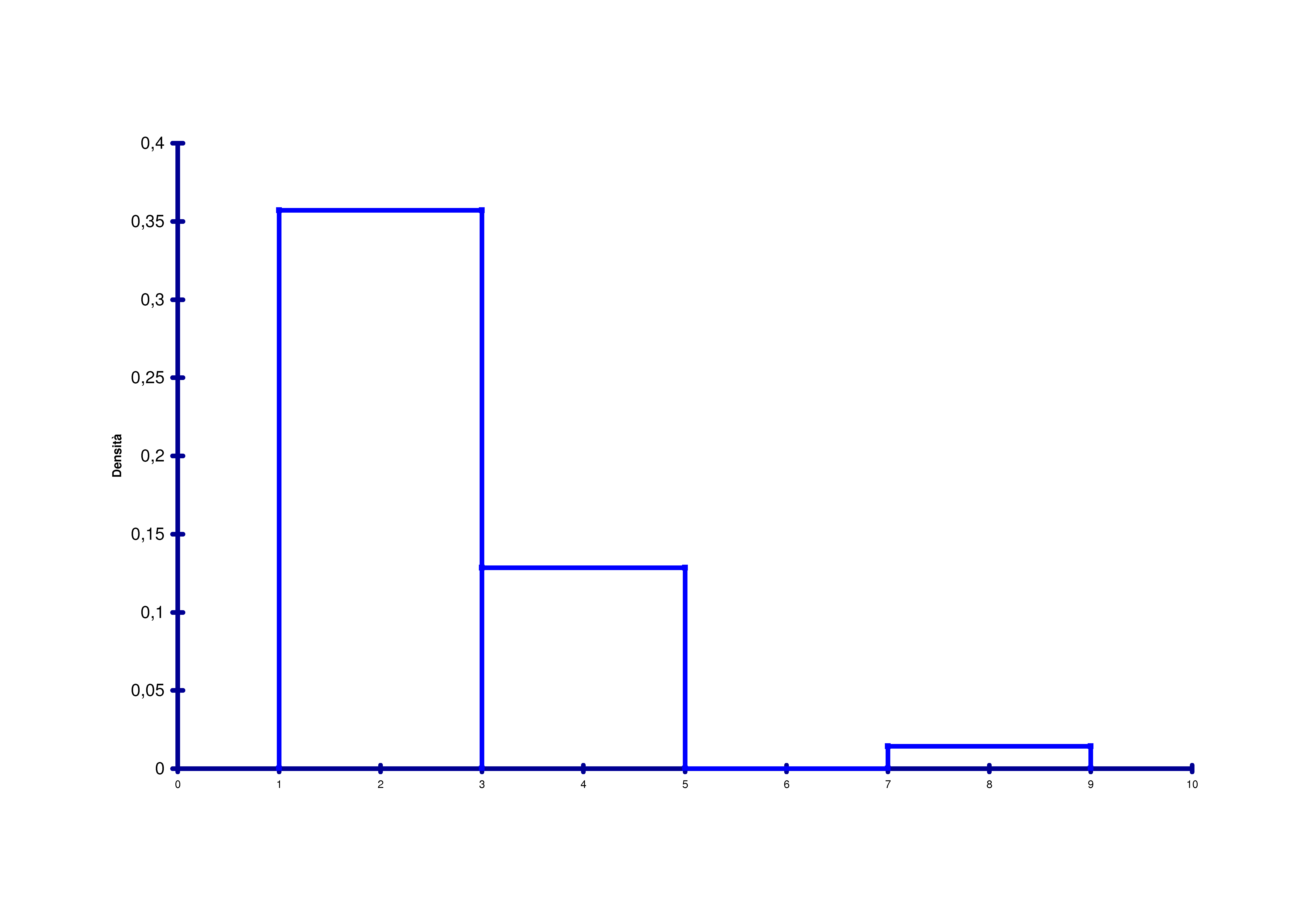
Distribuzione delle frequenze e istogramma con classi di ampiezza uguale.
Nel grafico la scala delle ordinate riporta le intensità.
| Classi | n | f | I | ||
|---|---|---|---|---|---|
| 0 | - | 2,0 | 4 | 0,114 | 0,057 |
| 2,0 | - | 2,5 | 6 | 0,171 | 0,343 |
| 2,5 | - | 3,0 | 15 | 0,429 | 0,857 |
| 3,0 | - | 5,0 | 9 | 0,257 | 0,129 |
| 5,0 | - | 8,0 | 1 | 0,029 | 0,010 |
| Totale | 35 | 1,000 | |||
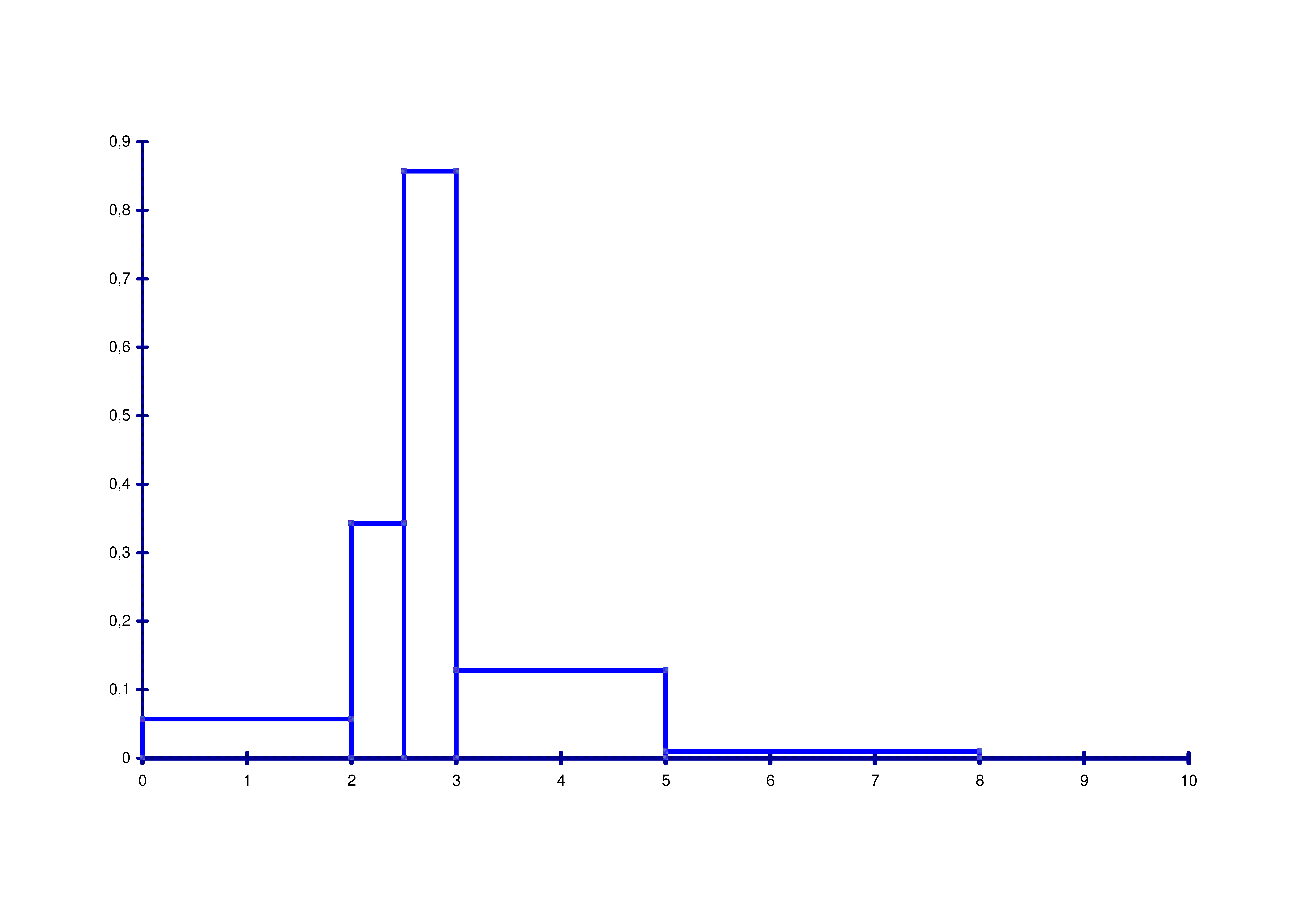
Distribuzione delle frequenze e istogramma con classi di ampiezza diversa.
Nel grafico la scala delle ordinate riporta le intensità.
-------------------------------------------------
Dal confronto dei due istogrammi appare evidente che in questo caso è preferibile adottare classi di ampiezze differenti
